2021年新高考I卷第21题赏析与圆锥曲线的切割线定理

华南师范大学附属中学(510630)罗碎海

2021年高考落下帷幕,一线教师高考研究的热情进入高潮.每年的高考题会出现一批批立意新颖充满趣味的好题,2021年新高考I 卷数学第21 题就是一例,值得欣赏,值得推广.

1 原题赏析

题目(2021年新高考I 卷第21 题)在平面直角坐标系xOy中,已知点点M满足|MF1|−|MF2|=2.记M的轨迹为C.

(1)求C的方程;

(2)设点T在直线上,过T的两条直线分别交C于A,B两点和P,Q两点,且|TA|·|TB|=|TP|·|TQ|,求直线AB的斜率与直线PQ的斜率之和.

读完该题,有几个问题值得思考:

问题1 为什么题目给出的是双曲线的右支,不是全部,想考查什么?

问题2 题目中的等式|TA|·|TB|=|TP|·|TQ|,在完整的双曲线中是否仍然成立?

问题3 由等式|TA|·|TB|=|TP|·|TQ|,联想到圆的相交弦定理与切割线定理,那么在圆锥曲线中有对应的定理吗?

分析1第一问很简单.看到第二问,自然想到用韦达定理转化求距离.

评述(1)在此解法中,考虑到Δ>0,但此时直线AB与双曲线的两个交点A,B可能分别在双曲线左右两支上,这个Δ>0 与该题不等价.但无论是在双曲线一支上有两交点,还是在两支上各有一个交点,本题答案不变.

(3)如果以上两个细节要说清,比较麻烦.但该题结论对整个双曲线成立,与一支或两支无关,细节不清,答案不受影响.所以该题易做,得满分不易.

分析2对于第二问,看到|TA|·|TB|=|TP|·|TQ|,联系直线的参数方程中参数的几何意义,应该更易解答.

由题意可知,直线斜率k满足|k|>4,得到16cos2α−sin2α<0,16cos2β−sin2β <0,由|TA|·|TB|=|TP|·|TQ|,得sin2α−16cos2α=sin2β−16cos2β,⇔1−17cos2α=1−17cos2β ⇔cos2α=cos2β,因为α,β∈(0,π),且αβ,所以α+β=π,所以,两直线斜率k1与k2满足k1+k2=0.

评述该解法考虑直线与双曲线交于一支,但未说明点T的位置.由于答案不受影响,还是抓主要矛盾吧.也许出题人就是为了避免大家都得满分,用双曲线一支编题.

2 圆锥曲线中的相交弦与切割线定理

在以上高考题中,等式|TA|·|TB|=|TP|·|TQ|使我们联想到圆中的相交弦定理与切割线定理,那么,此定理在一般的圆锥曲线中怎么样?我们以椭圆为例分析.

2.1 圆的相交弦定理与切割线定理

圆中有一组优美的性质——相交弦、切割线定理:

(1)相交弦定理如图1,圆O的两弦AB,CD交于圆内一点M,则MA·MB=MC·MD.

图1

(2)割线定理 如图2,过圆O外一点M作圆的两条割线AB,CD,与圆相交于A,B,C,D,则MA·MB=MC·MD.

图2

考虑割线的特殊情况变成切线,得到切割线定理.

(3)切割线定理 如图3,过圆O外一点M作圆的一条割线交圆于A,B点,作圆的一条切线MT,与圆切点为T,则MA·MB=MT2.

图3

这三个定理是一个统一体,是过一定点作直线与圆有公共点的问题.定点在圆内还是圆外,交点是两个还是重合为一个.

2.2 探讨相交弦定理在椭圆中的形式

设点A,B对应的参数t分别为t1,t2,则

同理有

所以

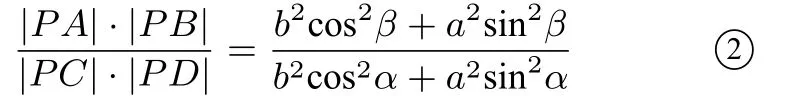
②式就是我们得到的椭圆割线的初步结果.在②中,若a=b,椭圆变为圆,②为圆的割线定理,;若β=π−α,也有,这是高中数学选修4-4《坐标系与参数方程》(人教A 版)P38 例4;从推导过程发现该关系在双曲线中依然成立,这正是文首今年高考题类型.

我们还发现①中比值只与椭圆长短轴长和直线的倾斜角有关,与点P的坐标倒无关.很自然想到取点P为椭圆中心,易得结果.但对抛物线来说没有中心,还是取椭圆的一个焦点更科学.

过焦点F作与l平行的焦点弦为MN,即在①中将(x0,y0)代为(c,0)得

同理分析其它圆锥曲线,得到以下统一定理:

定理3点P在圆锥曲线外(不含焦点的部分),过点P的直线l,m与圆锥曲线E分别切于点A和B,d1、d2为与l,m分别平行的焦点弦长,则.

到此,我们看到了圆的切割线定理在一般的圆锥曲线中的数学形式.从数与形的统一、特殊与一般辨证关系去分析问题,才能看到问题的本质与数学的发展规律,这也是我们学好数学的基本思想.高考题大多是将一般性问题特殊化、具体化.只要平时做好对每个问题特殊性与一般性分析,看高考题如掌上观纹.