从广州一模压轴题分析极值点偏移问题的发展

广东广雅中学(510160)赖淑明

极值点偏移问题自从2010年天津卷考查之后,近10年在各地高考题中经常见到它的身影,也掀起了一波研究热潮,关于极值点偏移问题的解法的研究,已经有很多同行在各大期刊发表过文章.极值点偏移问题似乎已经被套路化,解法已经程序化.然而,笔者认为极值点偏移的发展不会止步,因为双变量问题是中学函数导数问题的一大热点,而极值点偏移问题的解决办法为双变量问题的解决提供了依据和参考,是双变量问题的始祖.广州一模于3月19日结束,笔者受一模压轴题的这道极值点偏移题目的启发,思考极值点偏移问题的未来发展.

思路四主元法,把两个变量中的一个作为主元,转化为研究单变量问题.此方法对于不容易捆绑两个变量的双变量问题应用较多.本题因为捆绑比较简单就省略此解法.

四种解法的本质都是借助各种工具,把双变量问题转化为单变量问题解决.

题源1 与题源2 是极值点的本源问题,是过去考查的一般形式,本次一模题在此基础上作了两个调整:调整1:题干条件增加了两个零点的大小比较:x2>2x1;调整2:设问方式改为:.

从本题,我们可以窥见极值点偏移问题的如下几个发展的方向:

一、题干增加两个零点的大小比较,缩小零点的取值范围.

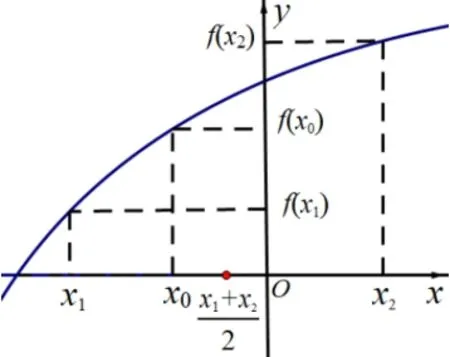
图1

图2

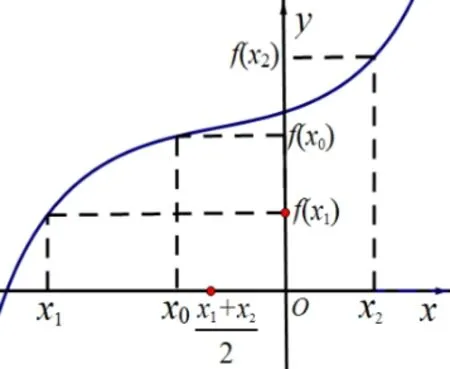
图3

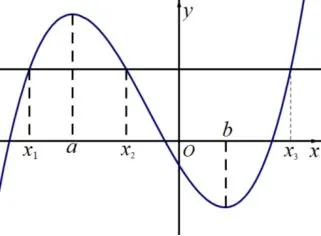
图4

图5