基于观测器的非线性多智能体系统的分组一致性
王 丹,李伟勋,张丽琼,刘 佳
(1.天津职业技术师范大学理学院,天津300222;2.天津职业技术师范大学自动化与电气工程学院,天津300222)
近几十年来,由于控制领域的快速发展,多智能体系统协同控制得到了各领域专家学者们的高度重视。多智能体系统协同控制应用有如下方面:一致性问题、同步、群集和蜂拥、编队控制以及聚集问题。其中,一致性作为最基础和最重要的问题,一直是控制领域研究的热点。一致性问题,即随着时间的演化,通过设计一个控制协议,使得复杂系统中所有智能体的状态达到一致。Hu等[1]研究了耦合通讯时滞下的二阶多智能体系统的领导跟随一致性问题。由于现实生活中,很多系统不一定是线性系统,当非线性取0时,即为一般线性多智能体系统[2],因而它能退化成任意阶的多智能体模型,故非线性系统的适用范围更广,且更具有一般性。如Shi等[3]提出非线性分布式控制协议,研究了非线性系统的领导跟随一致性问题。
实际生活中,智能体的状态不会全部达到一个相同的状态,往往是同一组智能体的状态相同,而不同组是另外一个值。Yu等[4]第一次提出分组一致性的相关概念,即相同子网的智能体达到相同的收敛状态,而不同子网间的智能体相互独立,并研究了一阶多智能体具有有向拓扑图的组一致性问题。组一致性作为一个新兴的课题,其为常规一致性的特例,且适用范围更广,所以研究分组一致性十分必要。王强等[5]在连通二部图的拓扑结构下,通过使用基于竞争的控制协议方法,分别研究了有时滞和无时滞下的一类多智能体系统的分组一致性问题;Cui等[6-7]研究了有向切换拓扑下二阶多智能体系统的分组一致性跟踪控制问题和通讯时滞下二阶多智能体系统的分组一致性问题。
鉴于大多数文献是基于邻居智能体的相关信息构建的一致性协议,而在实际操作中,由于成本或技术的原因,系统的某些状态变量并不是都可以直接检测,故需要设计基于邻域的分布式观测器。所谓分布式,是指当一部分跟随者和领导者之间无信息传递时,它们需要用分布式的方法从其邻居那里得到领导者的信息。Hong等[8-9]构造了一阶多智能体系统和二阶多智能体系统的基于分布式观测器设计的领导跟随一致性的追踪问题。针对智能体状态不可测的问题,刘忠信等[10]通过设计基于观测器的一致性算法,解决了一般线性系统的基于观测器的一致性控制问题。上述研究大多基于线性系统,针对非线性部分,Xu等[11]通过设计基于观测器的分布式非连续的一致性控制协议,研究了带有自适应耦合参数的二阶多智能体系统基于观测器的领导跟随一致性问题。Chu等[12]提出了一个非连续的观测器协议,利用矩阵理论、交换系统理论以及平均方法研究了一般线性系统带有Lipschitz非线性项的间歇通信非线性多智能体系统的一致性问题。
Han等[13]采用基于扰动观测器的方法抑制由外部系统造成的扰动,研究了具有外生扰动的多智能体系统的包含控制问题,虽然它们在动力学方程中都不止含有1个领导者,但此研究对一般线性系统带有干扰观测器的包含控制一致性问题进行了探讨,即一致性实现途径是跟随者的状态移动到由领导者构成的凸包中。与文献[13]不同,本文分别考虑线性和非线性系统基于分布式观测器的分组一致性问题,即将智能体分为2组,每组有1个领导者,并通过设计相应的控制协议,用基于观测器的方法观测每组智能体中跟随者智能体跟随领导者智能体的跟踪状态轨迹。
1 问题描述与预备知识
1.1图论
由于多智能体系统在协同各智能之间体有信息传递,其之间的信息交互可以通过拓扑图来描述[14],将每个智能体看作图的一个节点,从而使得结果更为直观。假设由n+m个智能体的加权有向图G表示为G=(V,E,A)。其中,每一个顶点表示一个智能体。顶点集合V={v1,v2,…,vn+m},有向边集合E⊂(vj,vi),每组智能体i的邻居节点集合为N1i= {j∈V1:(i,j)∈E,j≠i},N2i={j∈V2:(i,j)∈E,j≠i},将它们写成紧凑的形式得到Ni={j∈V:(i,j)∈E,j≠i}=N1i∪N2i。
非负加权邻接矩阵A=[aij]n×n,aij>0。当且仅当(vj,vi)∈E,即表示顶点vj能接收到vi的信息,否则aij=0。
度矩阵定义为D=diag{d1(v1),d2(v2),…,dn+m(vn+m)}。式中:D为第i个跟随者智能体与领导者智能体之间的连通矩阵。
平衡图是指所有节点的入度与出度相等,即degin(vi)=degout(vi),顶点vi定义为
图G的拉普拉斯矩阵定义为:L=D-A,Lij=
将n+m个智能体分2组。第1组:I1={1,2,…,n},V1={1,2,…,n}追踪第1个领导者;第2组:I2={n+1,n+2,…,n+m},V2={n+1,n+2,…,n+m}追踪第2个领导者。并且有I=I1∪I2,V=V1∪V2,E=E1∪E2。
定义1多智能体系统能够实现组一致性跟踪控制,如果满足以下条件
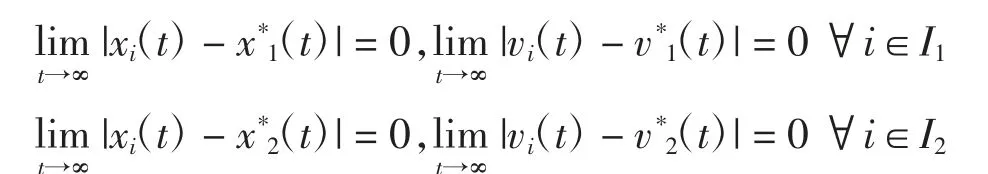
假设12组之间入度平衡[14]的条件为
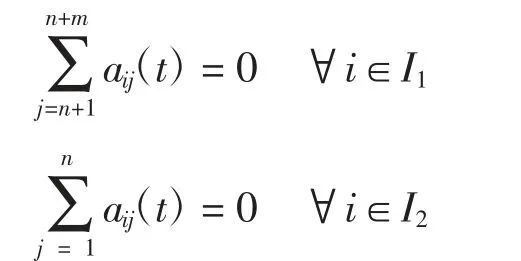
该条件保证了系统能达到分组渐近一致的条件,即不同组之间相互影响的权重之和为0。
1.2 模型构建
假设2存在非负常数ρ1和ρ2,使得
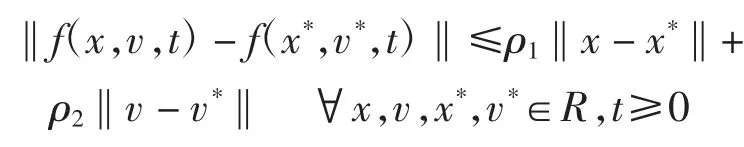
假设3对于每一个跟随者来说,都至少有一条路径与领导者连通。
引理1[15]对于任意的向量a,b∈Rn以及正定矩阵Φ∈Rn×n,下列不等式成立
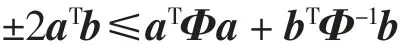
针对多智能体基于观测器的分组一致性分析,本文从非线性系统和线性系统进行阐述。
1.2.1 非线性系统
针对非线性系统,本文考虑有n+m个跟随者和2个领导者构成的多智能体系统的领导跟随一致性问题。其中,领导者的动态方程为

式中:x*j、v*j、f分别为领导者的位置、速度和非线性项,x*j∈R,v*j∈R,f(x*j(t),v*j(t),t);f:R×R×R。
跟随者的动态方程为
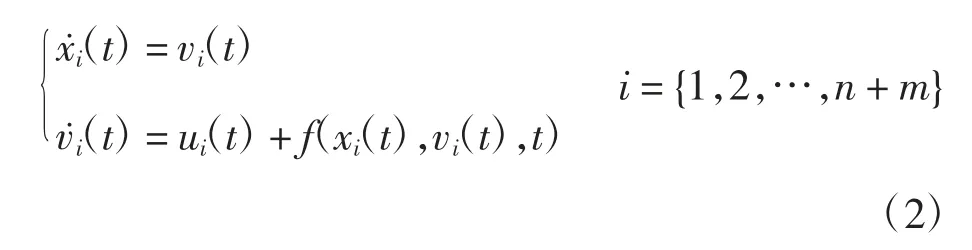
式中:xi∈R、vi∈R、f(xi(t),vi(t),t)分别为第i个智能体的位置、速度和非线性项;f:R×R×R。
针对非线性系统,由于部分跟随者智能体得不到领导者智能体的信息,故需要设计分布式控制协议,使得每个跟随者智能体利用其获得邻居智能体的信息,从而估计领导者的状态。控制协议如下
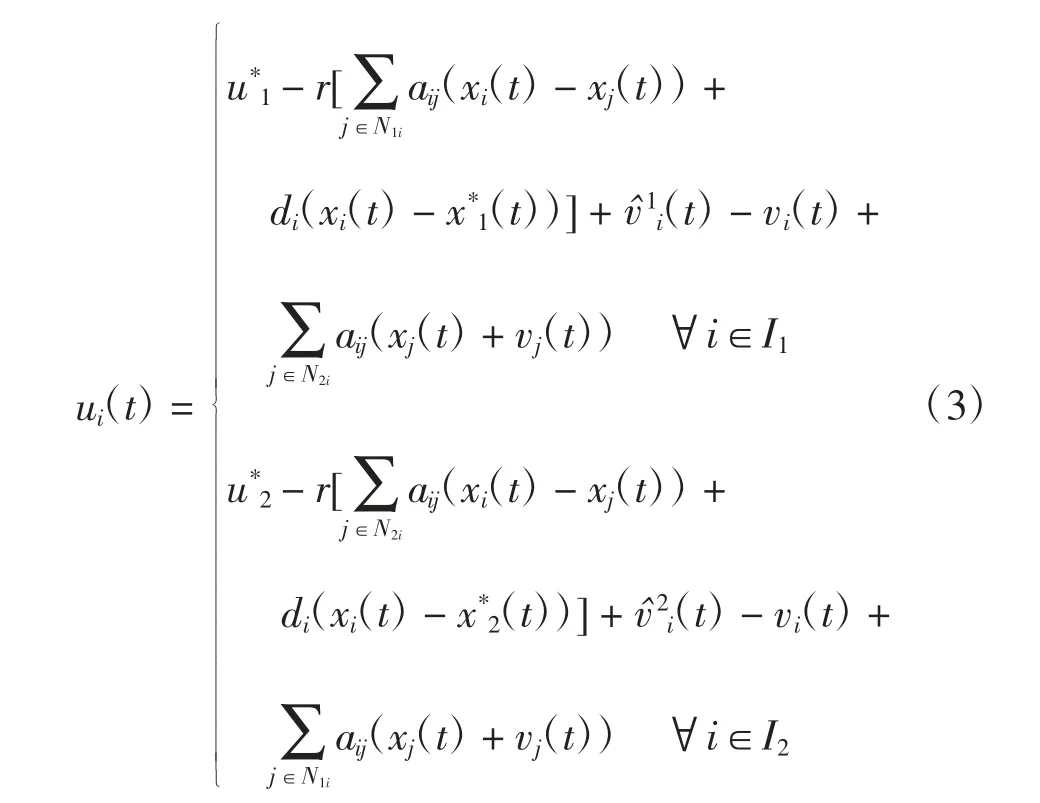
式中:r、c为给定的常数;以所设计的控制协议的第1组为例,u*1为第1个领导者智能体的控制输入;为第i个智能体与其邻居智能体状态误差的累加部分;di(xi(t)-x*1(t))为第i个智能体与领导者智能体状态误差项为第i个智能体对领导者速度的观测值与其速度的误差;为第2组对第1组的影响。
观测器下智能体的动态方程为
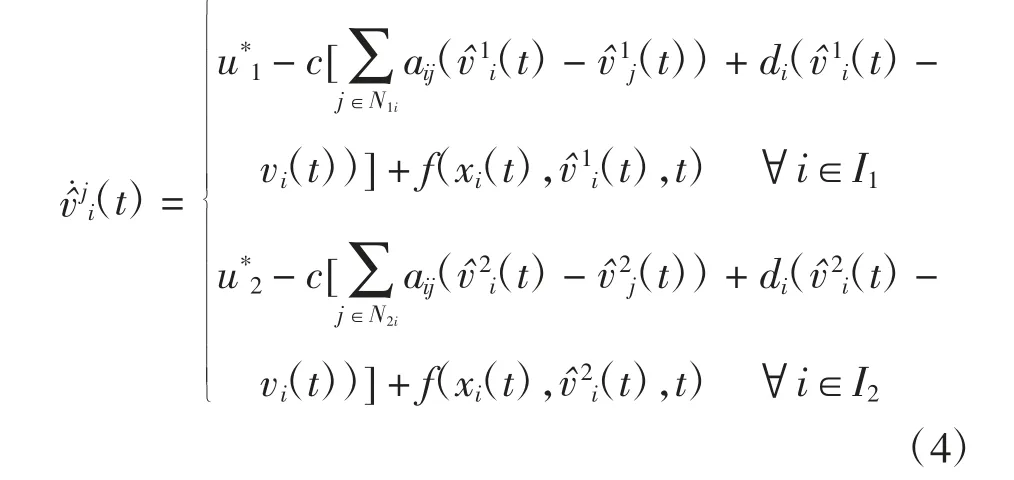
由于跟随者智能体得不到领导者的速度信息,故无法设计各跟随者与其领导者智能体之间的速度误差项,只能通过速度观测值误差进而估计跟随者与领导者的速度误差,这是区分本文中分布式观测器和分布式控制器设计的不同之处。
为了分析该二阶非线性多智能体系统能实现基于观测器的领导跟随组一致性问题,定义状态误差ξ1i(t)=xi(t)-x*1(t),(i=1,2,…,n);ξ2i(t)=xi(t)-x*2(t),(i=n+1,n+2,…,n+m),则有ξi(t)=[ξT11(t),ξT12(t),…,ξT1n(t),ξT2,n+1(t),ξT2,n+2(t),…,ξT2,n+m(t)]T,(i=1,2,…,n+m)。
定义速度误差η1i(t)=vi(t)-v*1(t),(i=1,2,…,n);η2i(t)=vi(t)-v*2(t),(i=n+1,n+2,…,n+m),则有ηi(t)=[ηT11(t),ηT12(t),…,ηT1n(t),ηT2,n+1(t),ηT2,n+2(t),…,ηT2,n+m(t)]T,(i=1,2,…,n+m)。
标记
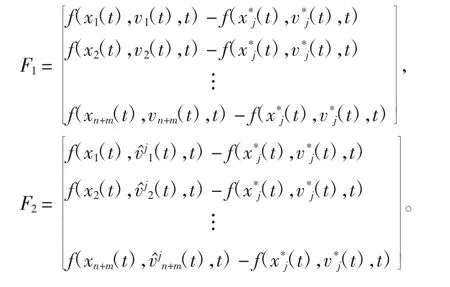
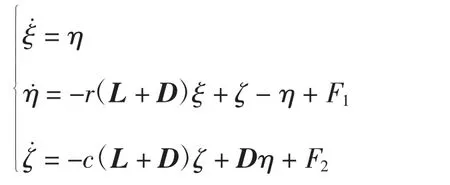
则闭环系统的误差方程可写为

其中,
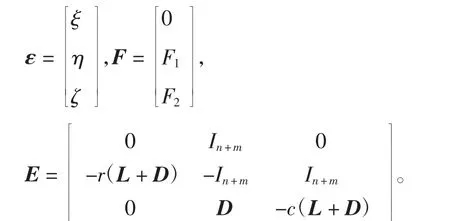
1.2.2 线性系统
针对线性系统,本文考虑有n+m个跟随者和2个领导者构成的多智能体系统的领导跟随一致性问题。其中,领导者的动态方程为
式中:x*j∈R和v*j∈R分别表示领导者的位置和速度。
跟随者的动态方程为
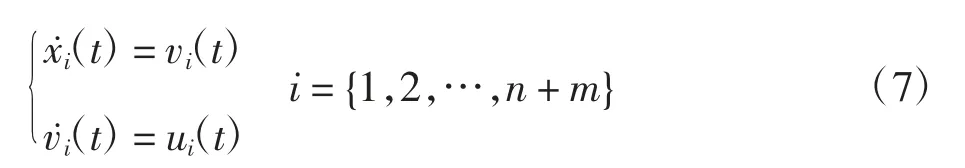
式中:xi∈R和vi∈R分别为第i个智能体的位置和速度。
针对线性系统,设计如下的分布式控制协议
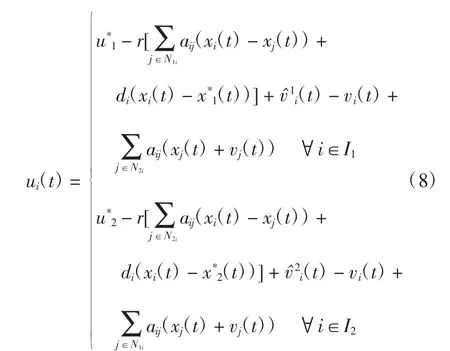
观测器下智能体的动态方程为
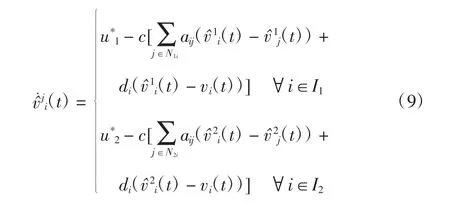
2 主要结果
以下的定理分别给出了基于观测器的非线性系统以及线性系统分组一致性实现的条件。
2.1 基于观测器的非线性系统的分组一致性
定理1考虑到给定的多智能体系统(1)、(2),系统满足所有的假设条件。在控制协议(3)和观测器(4)下,所有的跟随者能跟踪上领导者,并且跟踪误差趋于0,即表示所构建的二阶非线性多智能体系统能实现基于观测器的分组一致性,如果以下条件成立
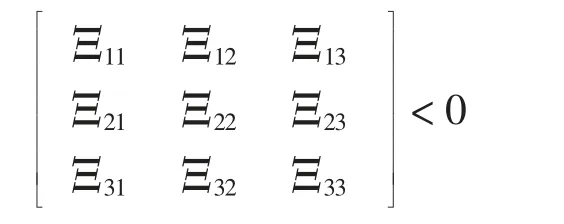
式中:
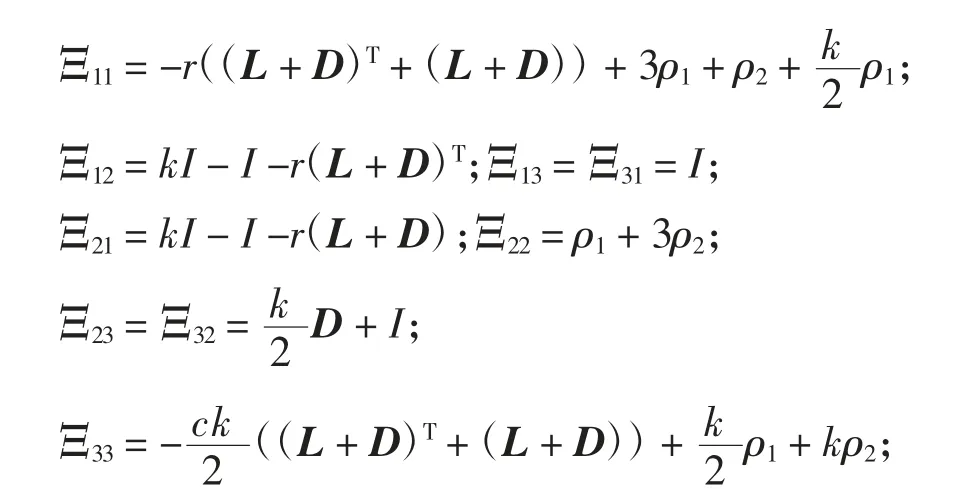
r、c为给定的常数;k∈R,k>1。
证明对于系统(1)、(2),选取Lyapunov函数为V=εTPε
对V沿着闭环系统的误差方程(5)求导,可得
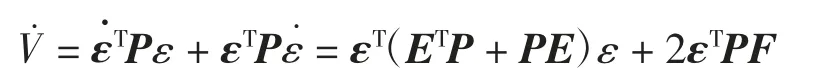
分别代入矩阵P、E、F计算得
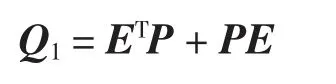
由引理1得
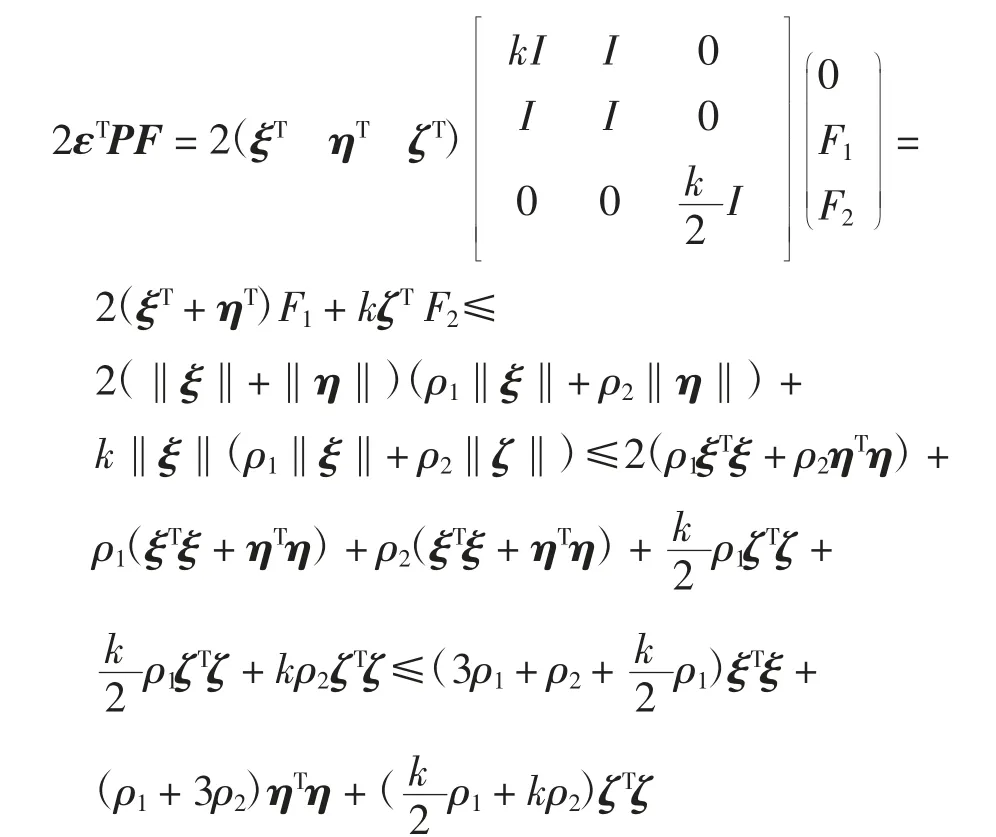
令
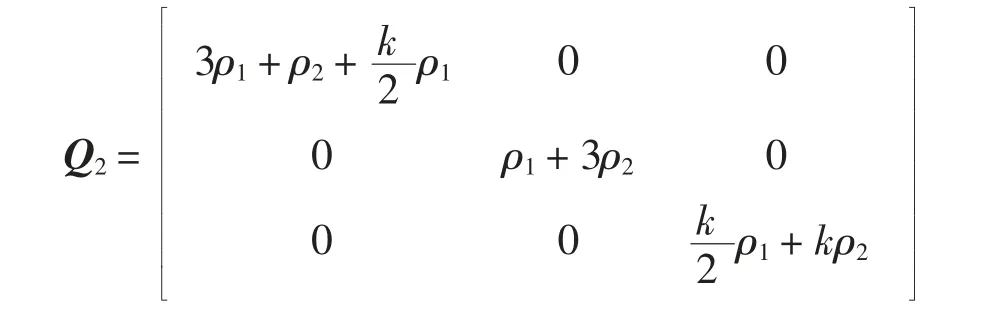
则
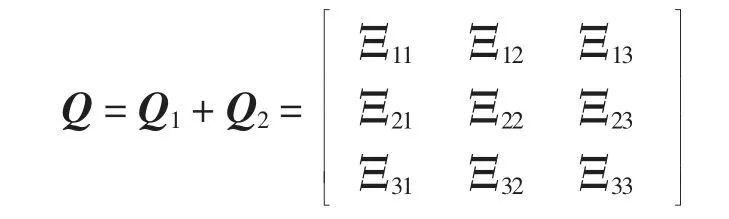
式中:
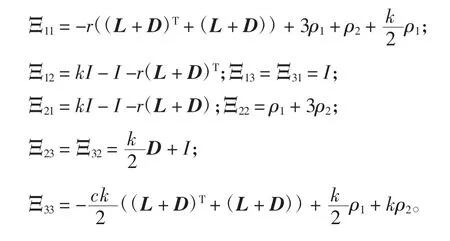
如果有Q<0,则可进一步得到V˙<0。因此,误差系统(5)能实现渐近稳定,即表示多智能体系统在状态协议(3)下能达到基于观测器的分组一致性。
2.2 基于观测器的线性系统的分组一致性
定理2考虑到给定的多智能体系统(6)、(7),系统满足所有的假设条件。在控制协议(8)和观测器(9)下,所有的跟随者能跟踪上领导者,并且跟踪误差趋于0,即表示所构建的二阶线性多智能体系统能实现基于观测器的分组一致性,如果以下条件成立
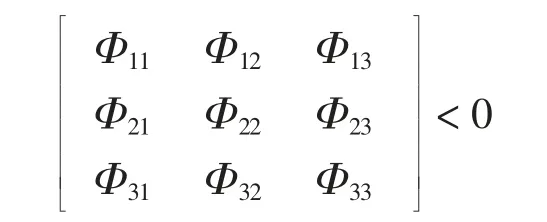
式中:
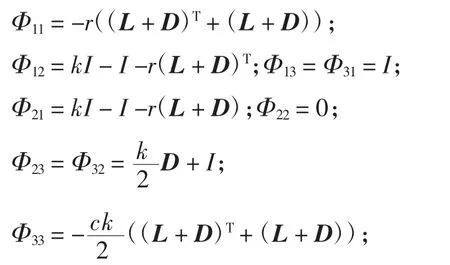
r、c为给定的常数;k∈R,k>1。
线性系统多智能体基于观测器的分组一致性证明和定理1类似,这里不再赘述。
3 数值模拟
在这一部分中给出了基于定理1和推论1的仿真实例。考虑了包含2个领导者和6个智能体的拓扑图,令智能体①②③为第1组,智能体④⑤⑥为第2组,它们分别跟踪领导者⑦和⑧。取r=0.4,c=0.2,针对所分的2组,选取不同领导者的控制输入分别为u1=5+0.5sin(t),u2=1+0.8cos(t)。跟随者的非线性项为f=-0.2sin(t)-0.6vi+2.25cos(2.5t)。
非线性系统状态图和误差图中各智能体的初始状态分别为

多智能体系统的拓扑图为固定拓扑,其拓扑图如图1所示。
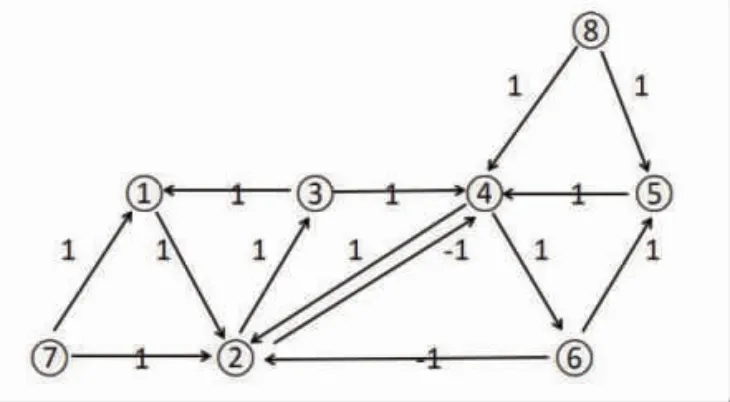
图1 多智能体系统的拓扑图
由图1可知,第1组的智能体①②能得到领导者⑦发出的信息,第2组的智能体④⑤能得到领导者⑧发出的信息,并且每组的领导者之间没有信息交流。从而进一步得出系统拓扑结构的邻接矩阵和跟随者之间对应的拉普拉斯矩阵分别为

以下为通过Matlab仿真给出的基于观测器下非线性系统多智能体的状态轨迹图以及其所对应的跟踪误差图,如图2—图5所示。
由图2、图3可知,每组智能体分别跟踪上了其对应的领导者。由图4、图5得到:位置误差、速度误差都可以在15 s内收敛到0,故该仿真实验可以验证本文所构建模型的合理性。
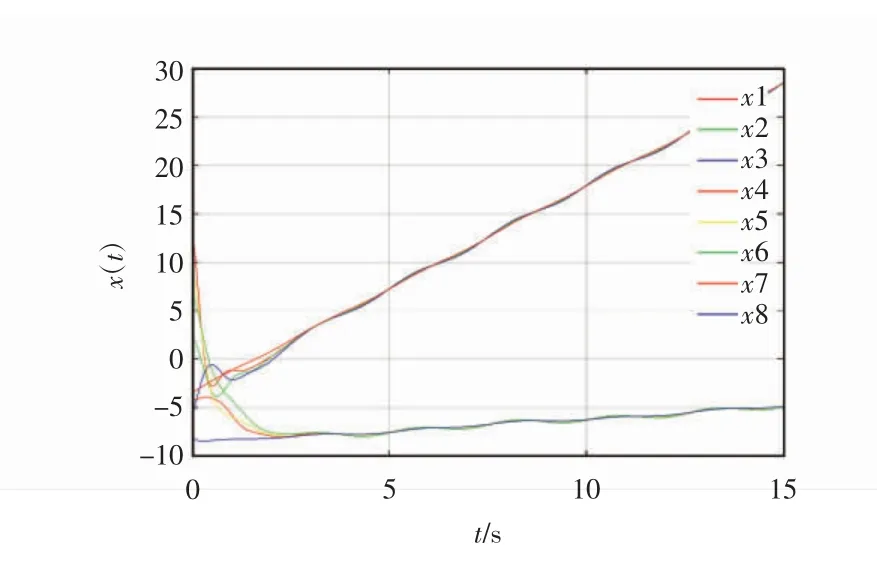
图2 分组一致性位置状态图
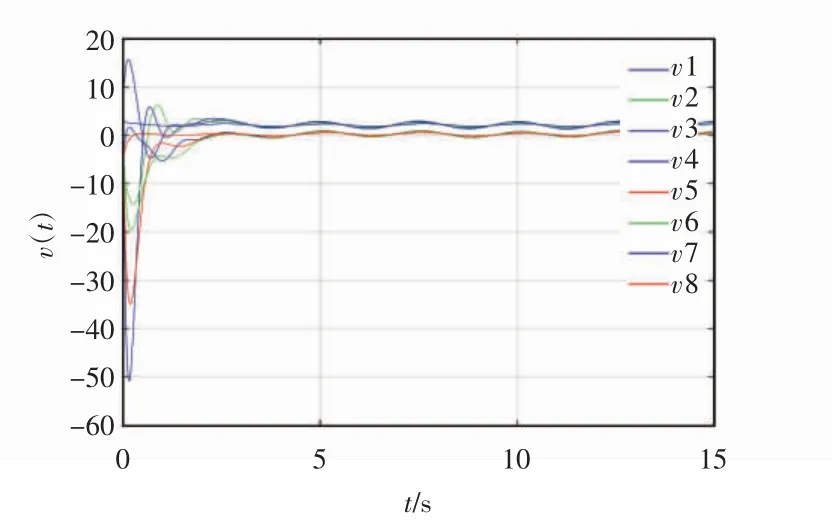
图3 分组一致性速度状态图

图4 分组一致性位置跟踪误差轨迹图
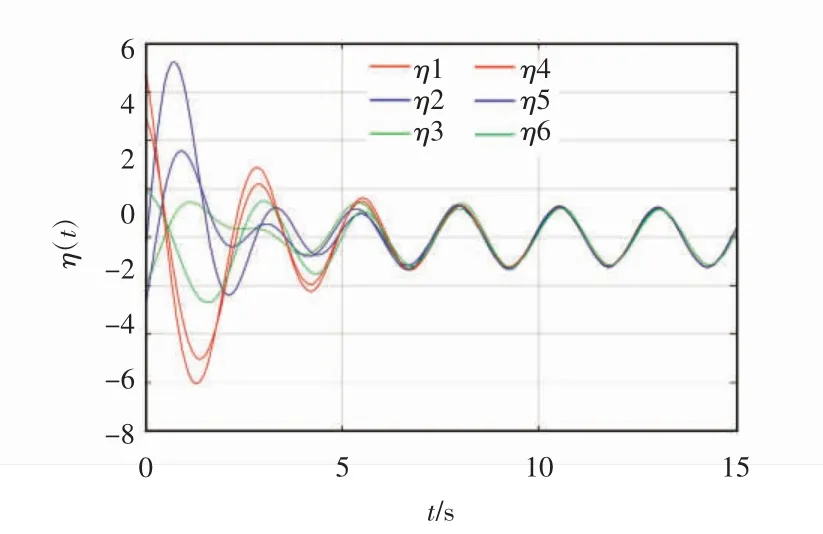
图5 分组一致性速度跟踪误差轨迹图
4 结语
本文研究了基于观测器的二阶非线性多智能体系统的分组一致性问题,针对多智能体系统中领导者的速度信息不可测的问题,设计了分布式观测器,即通过利用已知的、能观测的跟随者智能体的速度信息以及各跟随者智能体速度观测值与其速度的误差,进而估计跟随者与领导者的速度误差。为了实现分组一致性跟踪问题,基于观测器的相对输出信息,设计了分布式控制协议,通过构建合适的Lyapunov函数以及使用舒尔补等相关引理,分析了系统的稳定性,并由Matlab绘制出了非线性系统的状态图和误差图。结果表明,构建的模型既保证了观测器误差趋于0,也实现了分组一致性跟踪问题。
由于实际的多智能体系统的网络拓扑结构往往不是一成不变的,所以本文接下来将研究在拓扑结构为切换的情况下,基于观测器的非线性多智能体系统的分组一致性问题。由于本文考虑的是二阶系统并且智能体的维数是一维的,所以会进一步考虑如果系统是更高阶或者智能体的状态是高维的情况下,基于观测器的多智能体系统的分组一致性实现的问题。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

