基于模型分类算法的针刺神经电信号的统计分析
秦 晴,陈 伟,郑海令
(天津职业技术师范大学天津市信息传感与智能控制重点实验室,天津300222)
针刺穴位能够诱发神经系统产生响应活动,对神经和内分泌网络进行调节,进而提高靶器官的各项功能[1-3]。在针刺动物实验中,实验者将电极植入动物脊髓,采集针刺神经响应信号[3-4]。将电极植入目标区,采集电极周围神经元的胞外活动是神经科学中最常用的信号采集手段。由于电极采集的是周围神经元集群的放电活动,所以实验者的首要任务是对放电进行分类,将采集到的所有的动作电位分别归入相应神经元[5]。尽管放电分类算法的研究困难且耗时,但仍是相当必要的,这是因为对于特定的输入刺激,实验者不能把采集到的所有电信号放在一起作为该刺激的响应,对于不同的输入刺激,每个神经元个体不会呈现相同的放电活动。为了降低放电分类算法中的困难,早期实验者采用比较精细的电极植入目标区,并放在给定神经元最近的位置,降低其他神经元的放电干扰,但是该方法存在一些缺陷:电极偏向于靠近高幅值放电,即放电明显的神经元;由于电极的精细,其只能检测一个或少数神经元的放电活动[5]。
随着解剖学和生物物理学的快速发展,近期大多数的放电分类算法都是基于放电波形的。最早的基于放电波形的分类算法仅仅是基于动作电位振幅的分类处理,在很多情况下,振幅参数并不能将不同神经元的动作电位区分开。为此,基于放电波形的分类算法加入了时间窗的概念,定义1个或几个时间窗为特定神经元的放电波形,然后在时间轴上进行滑动对比,形状相同的放电波形就是该神经元的动作电位。但是,这种算法仍存在以下缺点:一是需要人为地选取作为参考的时间窗,这在成百个通道的分类处理中是不现实的;二是放电波形的叠加和背景噪声都能够导致放电波形发生变形,此时分类效果就会明显变差。变异的放电波形被剔除,大量的放电信息被遗漏。为解决变异波形的分类问题,本文在波形分类算法的基础上,采用一种基于模型的分类优化算法,该优化算法能够有效地辨识变异的放电波形,降低动作电位的漏检率,提高分类结果的准确性。
1 动作电位的分类算法
1.1 小波聚类算法
为了解决分类过程中人为导致的低效率性和误差等问题[6],文献[7-8]提出了基于小波变换(wavelet transform)和超顺磁聚类(super-paramagnetic clustering)的分类算法,简称小波聚类算法。算法分为3步:①设置阈值提取所有的动作电位;②对动作电位的放电波形进行小波变换,提取小波特征参数;③根据小波特征参数进行自动的超顺磁聚类分析,获取每个神经元的放电序列。
在第①步中,电极采集到的信号先经过一个高频滤波器(300~3 000 Hz),然后根据滤波后的数据自动选取放电阈值,提取全部动作电位。阈值方程为

式中:x为经过高频滤波的信号。
在第②步中,小波变换是对信号的时频分析,以最佳的时间和最佳的频域对信号做出最佳的解释,同时它不需要信号时刻地保持稳定性。小波变换被定义为

其中,Ψa,b(t)是小波方程,小波变换是小波方程与信号x的卷积。根据方程(2)和(3)可以得到小波变换的逆变换,重构信号x。
在第③步中,超顺磁聚类分析[7-8]基于概率统计知识的聚类方法,估计某个点与其临近点的相互作用关系,这里的点yi表示动作电位i的m维小波特征。点间的互相作用强度被定义为

式中:‖yi-yj‖2为2个点的距离;K为临近点的个数;a为临近点的平均距离。
根据互相作用强度得到这2个点是同一类的概率

式中:T为温度;〈δsi,s〉j为临近点的状态距离,决定了2个动作电位i和j是不是同一类,只有当〈δsi,s〉j≥0时,动作电位i和j才有可能是同一神经元的动作电位。
1.2 基于模型的优化算法
虽然小波聚类算法很好地解放了人为操作,极大提高了分类效率,但是在噪声干扰[9-11]和波形叠加[12-14]问题的处理上并不是很理想。尤其在波形叠加的情况下,小波聚类方法的漏检率很高。当神经元发生同步或近似同步放电时就会产生波形叠加,与背景噪声相比,波形叠加并不是随机事件,而是神经元集群网络活动的重要体现。所以,由波形叠加所导致的分类错误是高度系统化的,不能被忽视。本文采用一种基于模型的分类优化算法,辨识同步或近似同步放电产生的叠加波形[15]。
假设t时刻电极记录的动过电位是神经元集群中所有放电波形在t时刻以不同形式的线性叠加,建立t时刻动作电位的生成模型[15-16]为
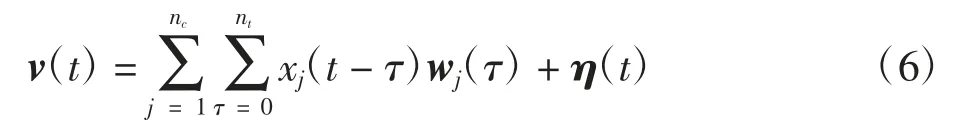
式中:列向量v(t)=(vi(t))ne×1为t时刻所有电极记录的动作电位;nc为多电极的个数;vi(t)为t时刻第i个电极记录的动作电位;所有的放电波形都被平均地离散成nτ份,矩阵wj(τ)为被所有电极记录的神经元j的第τ段波形;xj(t)为一个二进制变量,代表着神经元j在t时刻是否发生放电;η(t)为均值为0的背景白噪声。
根据方程(6),得到整个观测时间内的动作电位的生成模型

式中:W*X为方程(6)中的卷积运算;η(t)为一个多变量高斯白噪声。
故V-W*X服从多变量高斯分布,那么在放电时刻和放电波形条件下,动作电位产生的条件概率函数为
式中:Λ是多维高斯变量η的协方差矩阵,它不仅表示时间上噪声的协方差,还表示空间上电极采集位置所造成的噪声的协方差。
将小波聚类算法的分类结果作为优化算法的初始值,定义每个神经元放电序列xj和放电波形wj(τ)的先验概率函数。假设神经元放电是一个贝努利事件,那么xj(t)服从贝努利分布,且每个时间窗内都是独立的,放电序列xj的先验概率函数为
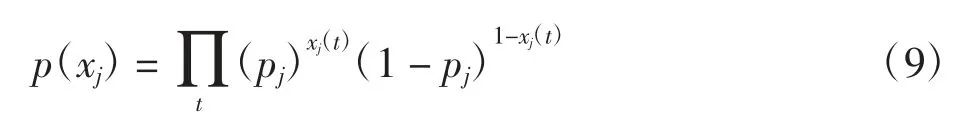
其中:xj(t)为一个二进制变量。t时刻神经元j产生放电时,xj(t)=1;否则xj(t)=0。从小波聚类方法的分类结果中可以获取神经元j产生放电事件的先验概率pj,如在针刺实验中,动作电位采样频率为40 000 Hz。如果小波聚类算法的分类结果中,针刺神经元平均每秒产生10个动作电位,即平均4 000个采样点就会产生1个放电,那么针刺神经元放电事件的先验概率为1/4 000。
根据先验函数、条件概率函数以及贝叶斯理论,动作电位由放电序列和放电波形诱发的后验概率函数为

令该后验概率函数取最大值,从而估计放电序列和放电波形[16-22]。
2 秩和检验
为了检验不同针刺手法的差异性,本文基于模型优化算法,对20次实验的分类结果进行秩和检验。在秩和检验中,原假设H0是针刺补法和针刺泻法所诱发的响应活动,没有显著差异。通过比较20次实验中捻转补法(“nb”)和捻转泻法(“nx”)所诱发的放电个数,可得到“nb”的秩和。同样地,通过比较20次实验中提插补法(“tb”)和提插泻法(“tx”)所诱发的放电个数,可得到“tb”的秩和Ttb。由于样本容量=20(nnb=nnx=ntb=ntx=20),因此秩和的分布接近正态分布。在这种情况下,可以采用Z检验,其基本公式为
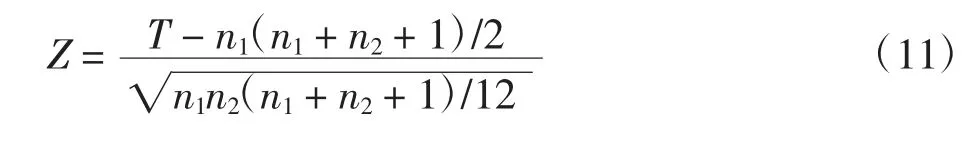
若显著性水平α定义为0.05,则根据正态分布的Z值表,可得H0得到的接受域为|Z|<1.96。如果Znb和Ztb均不在该接受域内,H0被拒绝,这就意味着补法和泻法所诱发的响应活动具有显著差异性;否则H0是真,补法和泻法无差异性。
3 针刺电信号的分类
3.1 2种分类方法的比较
采用针刺大鼠足三里实验中脊髓背根处神经元集群的放电活动作为原始数据,分别进行2种算法的放电分类,并比较它们的分类效果。针刺试验中,选择健康的成年大鼠(体重180~200 g,年龄2~3岁)为实验对象。实验前,所有大鼠饲喂7 d,以适应实验室标准环境。实验过程中,先用20%氨基甲酸乙酯(1.5 g/kg)对大鼠进行深度麻醉,然后在解剖显微镜下,从L4背根的中枢端分离神经细束,将细束搭放在一对双极铂金丝记录电极上,再用BIOPAC-MP150生理记录仪对针刺诱发的脊髓背根神经元的放电活动进行记录。确定足三里穴所对应的脊髓背根神经纤维(L4)后,待神经纤维静息后,依次对足三里穴进行不同手法的针刺刺激。针刺手法分别为捻转补法(“nb”),捻转泻法(“nx”),提插补法(“tb”)和提插泻法(“tx”),针刺频率为100次/min。为排除针刺顺序对实验结果产生的影响,在实验过程中采取随机的施针顺序。每种手法刺激时间为0.5 min,然后留针5 min,待大鼠静息后,再进行另一种手法的针刺刺激。
小波聚类算法的结果如图1所示。图1(a)—(d)分别为“nb”、“nx”、“tb”和“tx”4种针刺手法诱发的原始数据。4种手法条件下所有放电波形的小波特征参数,如图1(e)所示,这是一个二维的散点图。图中小波特征参数分布在4个不同颜色的区域,所以这些动作电位相应地被分为4类,每一类的平均动作电位如图1(f)所示。在此,定义红色高幅值的动作电位是由神经元1产生,绿色余弦动作电位是由神经元2产生,蓝色正弦动作电位是由神经元3产生,青色低幅值放电是由神经元4产生。由于神经元1放电波形的幅值明显较高,所以神经元1的小波特征参数的分布区域离其他3类比较远。4种手法条件下,估计得到的4个神经元的放电率如表1所示。然后,将小波聚类算法的分类结果作为初始值,根据模型算法,对4组原始数据进行重新分类,估计结果如表2所示。

表1 小波聚类算法中4个神经元在4种针刺手法下的放电率 个/s

表2 模型算法中4个神经元在4种针刺手法下的放电率 个/s
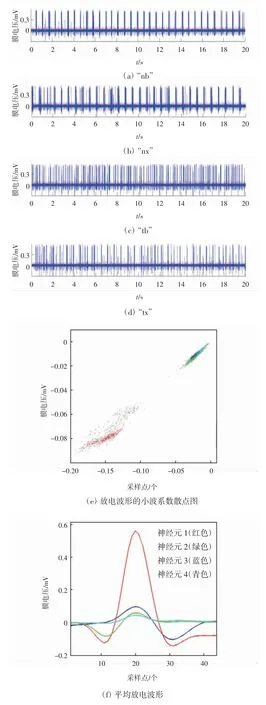
图1 小波聚类算法的结果
从表1中可以看出,在不同针刺手法条件下4个神经元放电率的差异性不大。从表2可知,在模型算法中除了神经元4,其他3个神经元被检测到的放电率均显著增加,有的甚至是小波聚类算法中放电率的2倍。而对于第4类动作电位,由于其幅值最低,且基电位过高,所以被认为不是神经元的响应活动,而是周围噪声的结果,所以4类动作电位不予考虑。为了更直观地体现模型算法的优点,选取2种算法在一次针灸刺激(约0.6 min)中的分类结果进行比较,电极采集的原始数据如图2所示,模型算法检测到的4个神经元的放电序列如图3所示,小波聚类算法检测到的4个神经元的放电序列如图4所示。
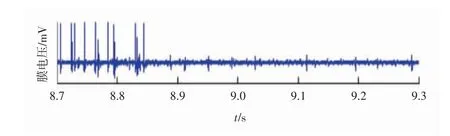
图2 电极采集的原始数据
从图3和图4可知,蓝色圆点是2种算法都检测到的动作电位。在图3中,红色圆点是模型算法多检测的动作电位,模型算法很好地解决了多个神经元放电叠加的问题。尤其是红色虚线框的部分,原始数据的膜电压集中地大幅度波动,表明神经元集群的响应活动强烈,此时模型算法能将所有的动作电位都检测出来,而基于放电波形的小波聚类算法却因为放电波形的多次叠加没有辨识出一个动作电位。另外,尽管小波聚类算法已经很好地解决了噪声的问题,但是与模型算法相比,仍有不足,如8.7 s附近的红色圆点(神经元1的高幅值放电),8.9~9 s和9.2 s附近的红色圆点(神经元3的放电),小波聚类算法都没有检测到,其所对应的膜电压曲线都存在动作电位的明显波动。在图4中,绿色圆点是模型算法漏掉的第4类动作电位。对于模型算法漏掉的动作电位(绿色圆点),其绝大部分分布在针灸刺激结束后的时间段,如绿色虚线框,同时其所对应的膜电压曲线在背景噪声范围内,所以这类动作电位被剔除。

图3 模型算法检测到的4个神经元的放电序列
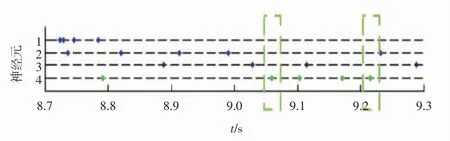
图4 小波聚类算法检测到的4个神经元的放电序列
3.2 4种针灸手法条件下神经元放电事件的统计分析
为了更加深入地研究不同手法刺激条件下神经元响应的差异性,本文运用模型分类算法对20次实验的原始数据进行分类处理,并对分类结果进行秩和检验,比较针刺补法和针刺泻法的差异性。秩和检验结果如表3和表4所示。
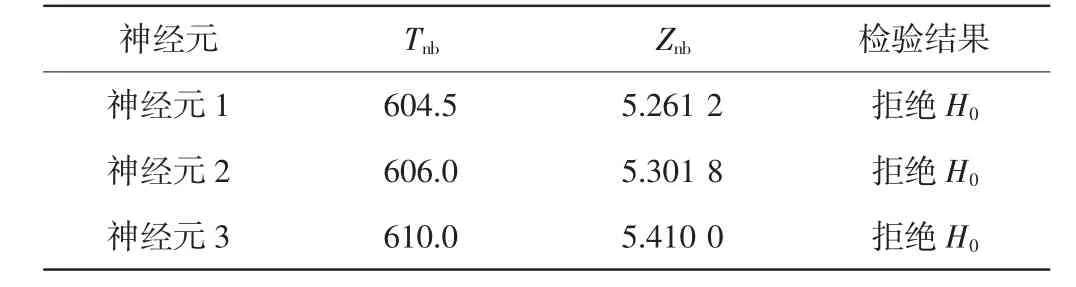
表3 “nb”和“nx”差异性的秩和检验

表4 “tb”和“tx”差异性的秩和检验
从表3和表4可以看出,捻转补法和提插补法条件下,3个神经元的Z值不在接受域内,均拒绝。这就意味着捻转补法和捻转泻法条件下3个神经元的放电活动都具有明显的差异性,提插补法和提插泻法条件下3个神经元的放电活动也具有明显差异性。
为了进一步揭示补法和泻法差异性的具体体现,本文对20次实验中神经元集群的放电事件进行统计分析。4种针刺手法条件下,3个神经元在20次实验中放电事件的统计结果如表5所示。

表5 4种针刺手法条件下3个神经元在20次实验中放电事件的统计结果 个/s
从表5可知,补法条件下3个神经元20次实验的平均放电率都分别大于相应泻法条件下3个神经元放电的平均放电率,其中第5行表示捻转补法条件下3个神经元在单位时间内多产生的放电个数,第6行表示提插补法条件下单位时间内多产生的放电个数。由此可得,补法和泻法条件下神经元响应的差异性在于补法能够诱发神经元产生较多的放电响应活动。
4 结语
本文根据针刺实验中电极记录的原始信号,采用基于模型的分类优化算法,克服了传统分类算法中波形变异和波形叠加问题,将脊髓背根处3个神经元的放电波形和放电序列准确高效地估计出来。同时,对多次实验中不同针刺手法条件下神经元放电事件进行秩和检验和统计分析。结果发现,针刺补法和针刺泻法产生的神经响应活动存在明显的差异性,在针刺补法条件下神经元放电响应活动明显多于针刺泻法。
——从一道浙江选考生物学试题谈起

