低剂量照射条件下CT影像快速重建算法研究
董 建,陈 昊,孟庆宽,秦转萍,杨耿煌
(天津职业技术师范大学天津市信息传感与智能控制重点实验室,天津300222)
随着计算机断层成像(computed tomography,CT)技术的发展,图像质量的明显改善,CT检查越来越多地被用于一些复杂疾病的诊断,并已经成为临床工作中不可缺少的影像学诊断工具[1-2]。然而,CT是一种放射性检查,具有电离辐射效应,患者过多地接受此类检查会导致电离辐射在人体内的积累,有引起癌变的风险[3]。因此,加速低辐射剂量的医用CT器械的研发已经成为医生与患者的共同期待。降低CT设备的辐射剂量可从改进硬件设备和开发重建算法两方面取得突破。近年来,CT设备制造商对其关键部件,如探测器、准直器、适形滤波器、自动曝光控制器等的技术更新,已经为降低辐射作出了重要贡献[4-5]。在图像重建方面,利用稀疏角度或受限角度投影数据、低管电压下的投影数据和非全局投影数据进行图像重建是在算法层面降低辐射的3个有效措施。近年来在该领域的论文数量增长迅速,也预示着超低辐射剂量CT的成像算法开发已成为研究热点之一[6-9]。本文聚焦利用低管电压下的投影数据进行图像重建的问题,对含有大量泊松噪声的投影数据进行重建。
投影数据的不完整性给图像重建带来了巨大挑战,搭载于现行CT机中的滤波反投影(filtered backprojection,FBP)算法重建出的图像含有大量噪声或放射状伪影,严重影响了正常组织结构和病变区域的刻画,甚至基本的迭代型算法如代数式重建(algebraic reconstruction technique,ART)和同步迭代(simultaneous iterative technique,SIRT)算法也无法获得满意的重建图像。2006年,Donoho等[10-11]提出了压缩感知(compressed sensing,CS)理论,为此类欠定问题的求解提供了理论依据。CS理论的求解机制一般要求先设计一个包含数据保真项和正则化项的目标函数,运用最优化理论实现目标函数的最小化,在此过程中得到所求数据的最优解。正则化项的设计对重建图像的质量起着至关重要的作用。全变分(total variation,TV)正则化在去除图像噪声、保存物体边缘方面能发挥有效作用,已经被视为该领域的优秀方案[12]。然而,越来越多的研究发现TV模型并不能完美重建所有类型的图像,尤其在重建含有较多高频信息的图像时表现出明显缺陷,如出现补丁状伪影、锯齿状物体边缘、丢失图像细节等[13]。因此,设计更优秀的正则化项已经变得迫在眉睫。近年来,深度学习技术也越来越多地被应用于低辐射剂量CT图像重建领域[14-15]。
本文创新了目标函数的设计方式,在TV正则化项的基础上引入基于非线性滤波的补充正则项。新方案使得非线性滤波操作与CS框架有机结合,进一步增强了算法对图像的重建能力。具体体现在TV模型只考虑中心像素与2个邻域像素的灰度相似度,而非线性滤波能将考虑范围扩展至包围中心像素的更大邻域范围。研究验证了4种非线性滤波分别嵌入CS框架后的新算法的重建效果,确认了新算法的有效性,利用凸优化领域的临近点算法对目标函数进行了最小化处理,构建出以行结构为基础的快速迭代算法,并利用腹部图像的重建验证了算法的收敛性。
1 腹部CT图像与投影数据
在人体各部分组织的CT影像中,腹部影像涵盖了人体的众多器官,像素的灰度跨度较大,而且图像中既包含了具有区域灰度一致性的较大面积器官,又包含了血管、胃肠容物、软组织褶皱等图像的细节信息。腹部影像可谓同时具备了众多的低频和高频信息,是用来验证图像重建算法性能的优质图像样本。本实验选取了腹部断层作为重建对象,对实际临床图像进行了去噪处理的实验用图像如图1所示。图像的像素数为512×512,像素灰度值反映CT值,其跨度范围为[-1024HU,2269HU]。

图1 人体腹部CT图像
人体腹部CT图像的投影数据如图2所示。图2(a)是图1所示腹部CT图像的投影数据,是在[0°,180°]范围内以180°/270的角度间隔进行的数据采集,因此该投影数据的像素数为512×270。此投影数据是对图1中图像进行再投影运算取得的数据,并非CT仪器中导出的图1图像重建前的原始投影数据。图2(a)的投影数据是在以平行束结构建模下取得的。本文聚焦低管电压下的投影数据的图像重建,向图2(a)的投影数据中加入泊松噪声,即可再现低管电压下的数据采集结果。图2(b)为光子数为4.0×106时引入了泊松噪声的投影数据。低管电压即代表了低剂量照射条件下的CT检查。

图2 人体腹部CT图像的投影数据
本研究选用C编程语言在Visual Studio 2017运行平台上进行了实现。所使用的PC机参数为Intel(R)Xeon(R)2.40 GHz 2.40 GHz的CPU处理器,32.0 GB内存,64位Windows 10教育版操作系统。
2 算法介绍
2.1 问题定义
CT图像重建即利用重建算法将投影数据转化为CT图像的过程。依据CS理论,本文设计了如式(1)所示的目标函数

式中:x=(x1,x2,…,xJ)T是一个J维向量,表示待求解图像;b=(b1,b2,…,bI)T是一个I维向量,代表已知投影数据;矩阵A代表I×J的系统矩阵,由CT装置决定;是L2范数型数据保真项,其保证待求解向真值逐步逼近是对图像进行滤波后又进行了稀疏约束;‖x‖TV是使重建图像具有分片光滑特性。两项操作均在去除了部分噪声后保留了图像的高频信息。2种范数的展开式为
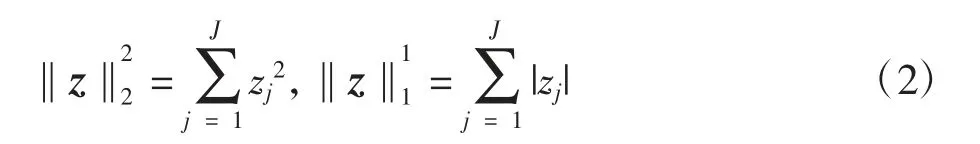
TV范数定义为
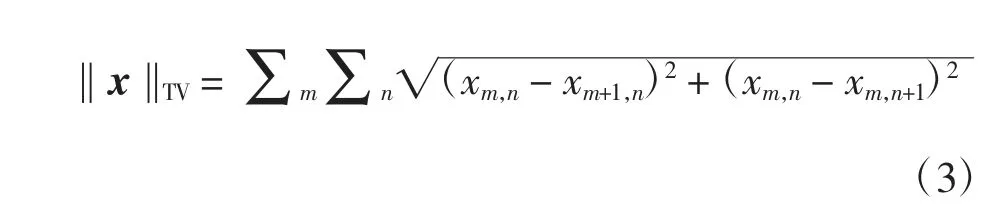
xm,n代表图像x在(m,n)处的像素值,本文仅在此处将图像看作一个二维矩阵以期对TV范数做直观说明。根据定义,式(3)可看作灰度梯度的L1范数,即因此TV范数也是一种特殊的L1范数。中的M操作代表对图像的非线性低通滤波,该正则化项使非线性滤波操作被引入CS框架,使非线性滤波的优势得以在CS中发挥重要作用,这也是本研究设计该正则化项的出发点。目标函数中的β和γ代表控制各正则化项作用强弱的超参数。为了使非线性滤波发挥优势以及抑制TV范数的缺陷,设定β取较大值,确定其主体地位,而γ取较小值,使TV项起辅助作用。
2.2 正则化项中的非线性滤波
本文重点验证了中值滤波、双边滤波、非局部均值滤波和非局部中值滤波分别嵌入正则化项后图像重建的效果。
中值滤波是一种基本的非线性滤波,它将中心像素点及其邻域的像素值由小到大排列,用位于序列的中间值代替中心像素的原有像素值。以同样的模式对图像中的每一个像素点进行遍历,完成中值滤波对图像的处理。中值滤波能有效去除脉冲性噪声,且在图像处理任务中能有效地保存图像中物体的边缘。
双边滤波是一种进化了的均值滤波,其首先计算中心像素及其邻域像素的权重,再用求出的加权平均值代替中心像素的原有像素值。以同样的模式对每一个像素点进行遍历。和传统的图像平滑算法不同,双边滤波在计算权重过程中除了考虑像素间几何距离上的接近程度外,还考虑像素间灰度的一致性。这使得双边滤波不仅能有效地去除噪声,还能保存图像上的边缘信息。
非局部均值滤波在双边滤波的基础上更强调像素块间的灰度一致性,非局部均值滤波的搜索窗口与像素块的示意图如图3所示。

图3 非局部均值滤波的搜索窗口与像素块的示意图
黄色部分是以像素xj0为中心的搜索窗口,橙色和蓝色部分是分别以xj0和xj0′为中心的像素块。搜索窗口的中心像素的像素值应被窗口中每个像素的加权平均值替代,因此计算搜索窗口中每个像素的权重成为关键环节。权重的大小由2个因素决定,分别为中心像素xj0与搜索窗口中某一像素如xj0′间的高斯距离,另一因素为分别以xj0和xj0′为中心的像素块的灰度相似性。像素xj0′的权重wj0′的计算公式为
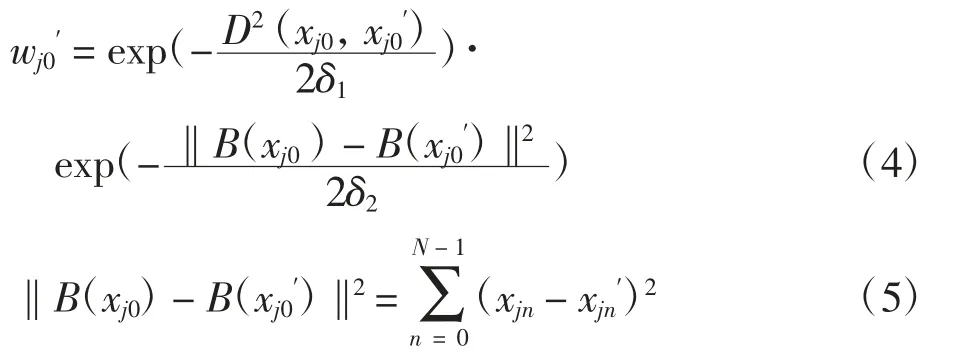
式中:D2(xj0,xj0′)为像素xj0与xj0′间的高斯距离;N为像素块中的像素数;参数δ1和δ2用来控制距离因素与灰度相似度因素对wj0′的贡献度。
非局部中值滤波中搜索窗口与像素块的选取策略以及搜索窗口中像素权重的计算方法与非局部均值滤波一致。当式(6)中的不等式成立时,以像素xjs′代替中心像素xj0,式中S代表搜索窗口中的像素数。

2.3 算法推导
为了构建快速的行处理型重建算法,本研究将目标函数中的数据保真项按系统矩阵的行进行拆分,见式(7)和式(8),并且用函数g(x)和h(x)分别代表2个正则化项。
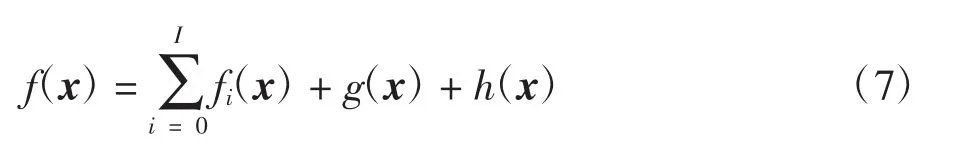

其中:向量ai代表系统矩阵A的第i个行向量,aiT是向量ai的转置。目标函数f(x)的最小化过程将用到凸优化理论中的重要工具,即临近点算法。文献[16]对该理论进行了详细介绍,本文不再赘述。由临近点算法推导得出算法执行过程如下

其中:k代表总循环次数,式中关于x的各种符号代表各中间过程图像。由式(9)可知,在变量i的循环过程中,任何一个投影数据元素bi均能促成一次图像的更新。只要程序的执行遵循特定的数据访问顺序,该算法就能像ART算法一样具有快速收敛性质,文献[17]对数据访问顺序的设计做了详细说明,本实验亦采用该类数据访问顺序。prox算子中的α(k)代表步长参数,为了避免数据陷入极限环,令α(k)=α0/(1+ε·k),α0和ε取值依具体任务确定。为了在图像平滑和去噪的同时达到程序快速收敛的效果,算法引入了跨度参数P,使得在数据保真项作用的间隙让2个正则化项依次起作用。式(9)还不具备算法的显式表达,以下将对算法中各个prox算子作出说明。
根据临近点算法,关于fi(x)的prox算子展开如下
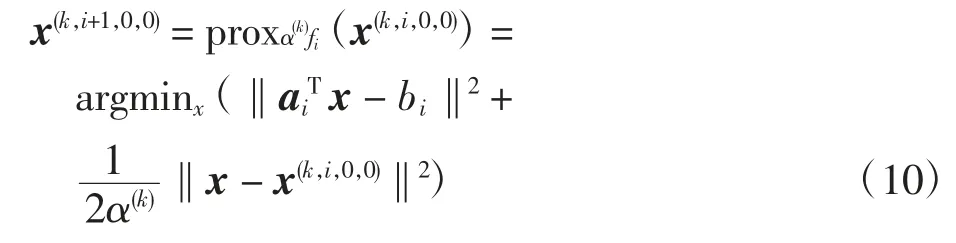
对式(10)求解,可得到如下迭代式

函数g(x)的prox算子展开如下
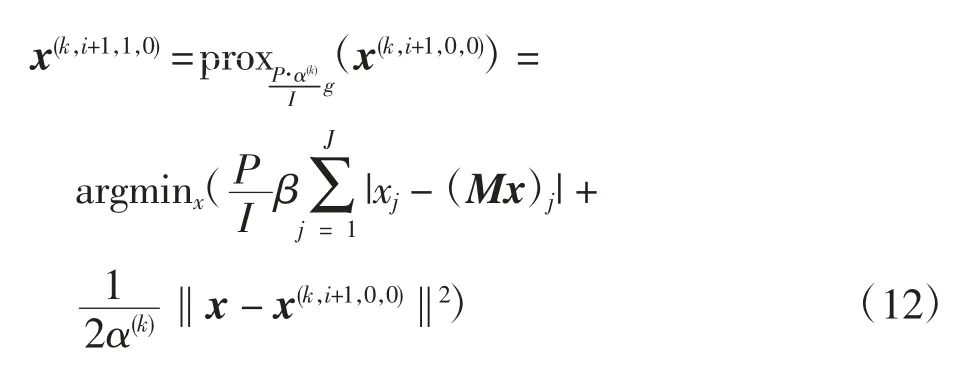
其中,Mx的存在(x是待求未知量,无法对其进行滤波操作)阻碍了式(12)的最小化。当步长参数α(k)取值足够小时,x无限接近已知量x(k,i+1,0,0)。因此,在α(k)取值足够小的前提下,Mx可由当前图像的滤波结果Mx(k,i+1,0,0)代替。至此,式(12)的求解可由封闭形式的软阈值处理实现,可得到迭代式

函数h(x)的prox算子展开如下
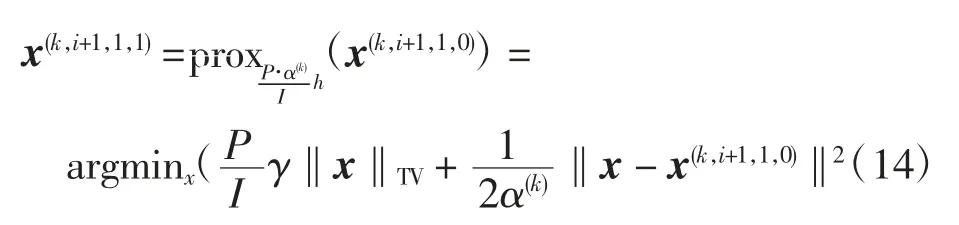
式(14)要实现TV项与二次项和的最小化,此问题形式是一个在CS领域常见的最优化问题。可将其看作是以x(k,i+1,1,0)为输入图像的TV项约束的图像去噪问题,被称作Chambolle投影算法的标准化算法可用于该问题的求解,此处引用了该算法[18-19]。
至此,低剂量照射条件下CT影像的行处理型重建算法已经构建完成。
2.4 算法展示
初始化 输入像素数为N×M的投影数据b。设置步长参数的控制变量(α0,ε)。设置β>0,γ>0的超参数以及P>0的跨度参数。
步骤1 赋值总循环次数k=0,像素数为N×N的初始图像x(0)=0。
步骤2 计算步长参数α(k)=α0/(1+ε·k),令x(k,0,0,0)=x(k)。
步骤3 图像更新程序:

步骤4 令x(k+1)=x(k,i+1,1,1),返回步骤2。
输出 当循环条件被满足时,输出图像x(k+1)。
3 实验结果及分析
3.1 传统算法重建结果
首先,本文用搭载于现行CT机中的FBP算法对低管电压采集条件下的投影数据(图2(b))进行重建,重建结果如图4所示。结果显示,有大量噪声传递到腹部的断层影像,各组织中的细节信息被覆盖,严重损害了该断层影像的临床诊断价值。

图4 FBP算法的重建结果
其次,本文用CS领域的经典算法TV最小化算法进行了图2(b)的重建实验,即只允许式(1)中目标函数的数据保真项和TV项起作用,令β=0。步长参数的控制变量α0=10,ε=1 000,跨度参数P=9×512,总循环次数k=50。本文对TV项的超参数γ的取值进行了探索性实验,代表性结果如图5所示。图5(a)为γ=1.0时的重建图像,图5(b)为γ=100时的重建图像。结果表明:γ取值小则TV项无法达到去噪效果,γ取值大则TV项对图像过度平滑,使图像细节消失以及出现锯齿状边缘。γ的其他取值亦未带来满意的重建效果。
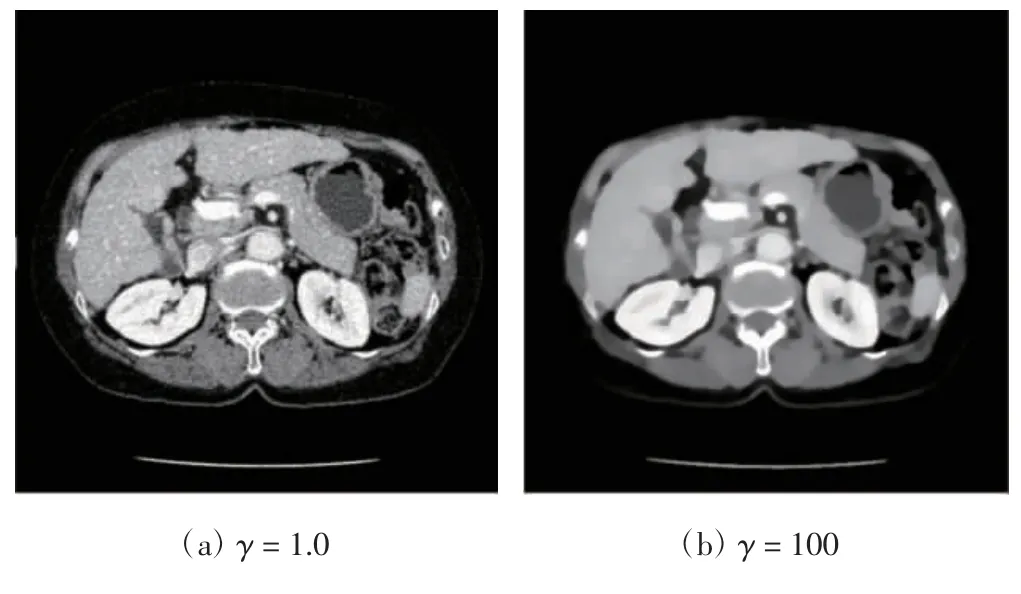
图5 TV算法的重建结果
3.2 新算法重建结果
图6为本文提出的基于非线性压缩感知4种算法的重建结果。
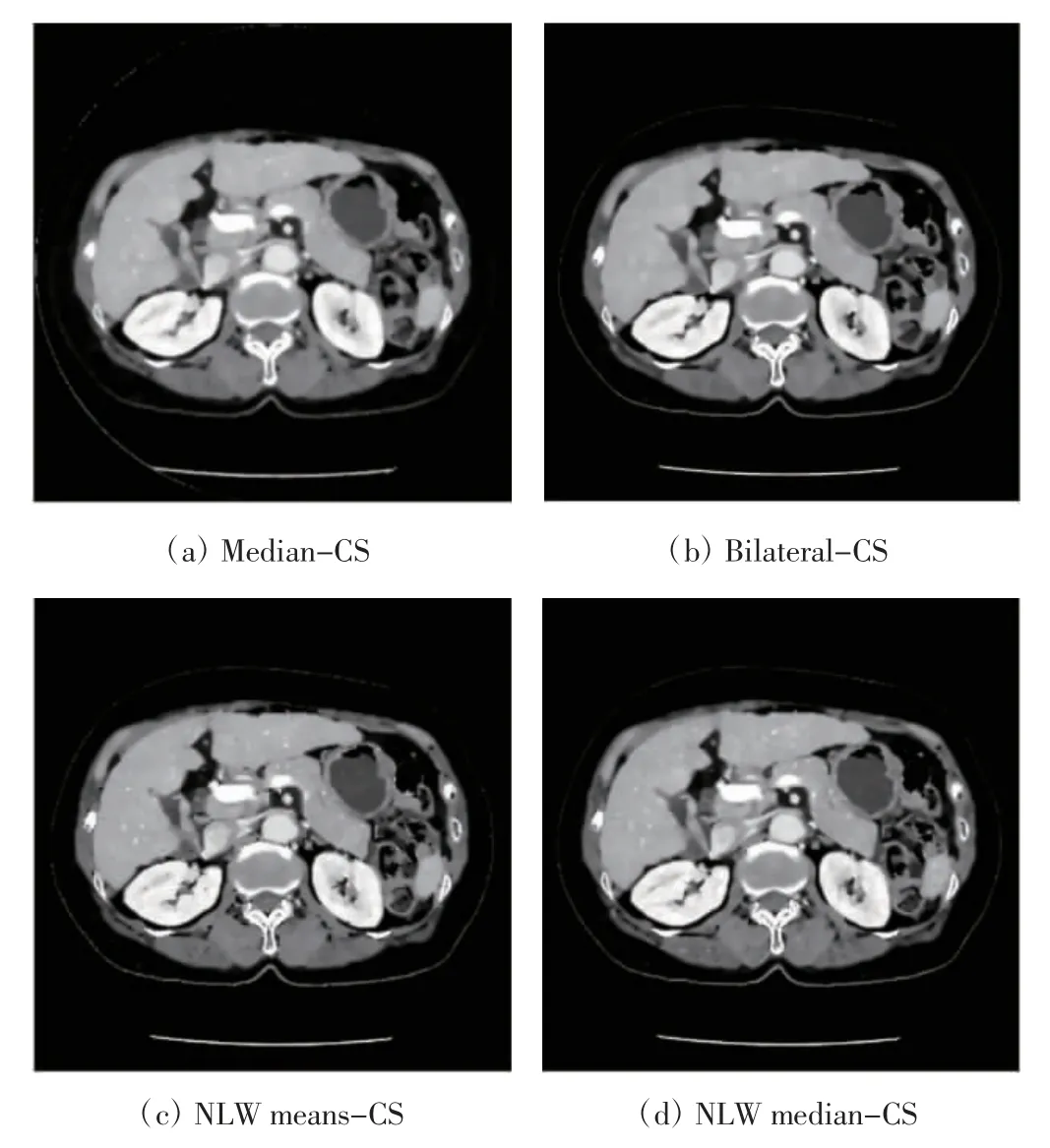
图6 新算法的重建结果
实验所选定的4种情况的共同参数:α0=10,ε=1 000,β=1 500,γ=20,P=9×512。图6展示的是各实验的第50次的运行结果。图6(a)的实验中,所设置的中值滤波器的搜索窗口为5×5。由图6(a)可知,Median-CS算法对图像进行了较好的去噪,然而其导致了部分图像细节的丢失,如肝脏中的血管信息。同时,结果图像类似于TV算法的结果,出现了部分锯齿状边缘。图6(b)的实验中,双边滤波的搜索窗口为5×5,设置δ1=10 000,δ2=120。由图6(b)可知,Bilateral-CS算法使图像获得了良好的平滑效果,然而图像的细节被过度平滑而失真。图6(c)的实验中,非局部均值滤波的搜索窗口和像素块的大小分别为7×7,5×5,设置δ1=δ2=45。由图6(c)可知,NLWmeans-CS算法使图像获得了较好的平滑效果,保存了图像的细节信息,但在图像的高频区域有密集性噪声残留,在图像的低频区域有分散性噪声点残留。图6(d)的实验中,非局部中值滤波的搜索窗口和像素块的大小分别为7×7,5×5,设置δ1=5,δ2=1 000。由图6(d)知,NLWmedian-CS算法获得了最好的图像重建效果,不仅对图像的噪声去除较完善,还较好地保留了图像的细节信息。
图6(b)—(d)的重建结果中,对图像的高频部分出现密集性噪声残留的机理阐述如下:在非局部滤波中,设定的搜索窗口中每个像素的权重由2部分因素决定,除了与中心像素的距离因素相关外,还与中心像素块的灰度相似度因素有关。距中心像素越远、与中心像素块的灰度值差距越大,该像素获得的权重越小。当中心像素处于灰度变化缓慢的低频区域时,其周围像素容易获得较大权重,因此中心像素能够达到良好的平滑效果。而当中心像素位于灰度变化急促的高频区域时,其周围像素获得的权重过小,故不能使中心像素达到有效的平滑效果,导致在高频区域出现密集性噪声残留。也正是得益于此项特性,图像高频区域的细节信息才得以较好地保存。而图6(a)的中值滤波不属于非局部滤波,不计算搜索窗口中像素的权重,因此不能依据图像的性质进行选择性的图像平滑。
3.3 图像与算法评价
为了更好地评价图像重建算法的效能,本文引入了均方根误差(root mean square error,RMSE)和峰值信噪比(peak signal-to-noise ratio,PSNR)2种图像的客观评价指标[20],其定义为

式(15)中xj和分别代表重建图像和参考图像的第j个像素的像素值。RMSE反映的是图像间的差异程度,是一种基于像素误差的图像质量客观评价指标,用于衡量被处理图像与理想参考图像之间的差异。RMSE值越小表示被处理图像的质量越好。式(16)中max(x)表示图像x中的最大像素值。PSNR是一种基于误差敏感的图像质量评价指标,其值越大表示被处理图像的质量越好。
表1为3.1与3.2中各实验结果图像的RMSE值和PSNR值以及迭代型算法的运行时间(设定总迭代次数k=50)。由表1可知,NLWmedian-CS算法的结果图像获得了最小RMSE值和最大PSNR值,表明该算法对图像的重建效果最佳,这与3.2中的主观观察结果一致。算法的运行时间方面,基于非线性压缩感知的图像重建算法的时间成本较高,且运行时间与算法所选择的非线性滤波器种类有关。

表1 结果图像评价指标与算法运行时间
另外,本文验证了基于非线性压缩感知的图像重建算法的收敛性,记录了各次迭代结果图像的RMSE值和PSNR值随迭代次数的变化情况。图7为NLW means-CS算法的运行过程中RMSE值的变化轨迹,图8为该算法的运行过程中PSNR值的变化轨迹。由图7和图8可知,算法运行到第10次前后便已经收敛到特定区间。因此,图示结果支持本文选取各个实验的第50次迭代的运行结果作为结果图像。
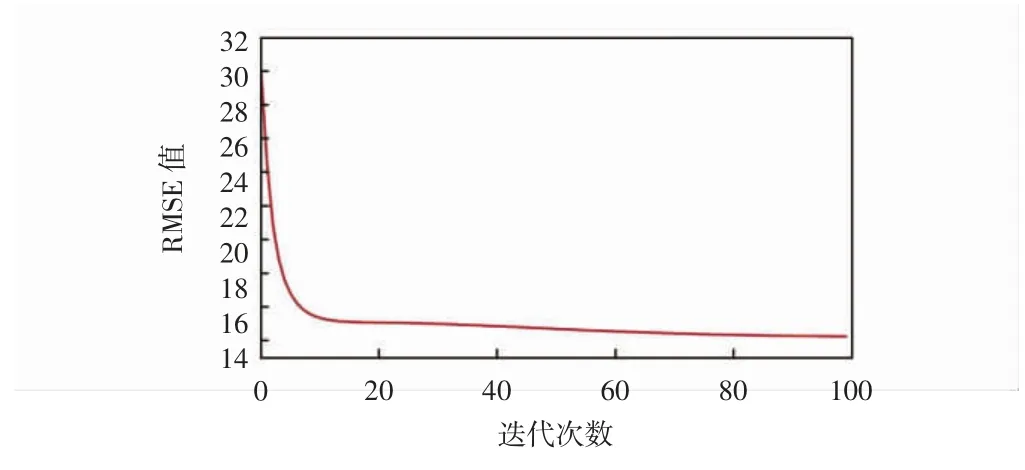
图7 RMSE值随迭代次数的变化

图8 PSNR值随迭代次数的变化
4 结语
本文研究了低剂量照射条件下基于非线性压缩感知的CT影像重建算法的开发问题。对低管电压条件下所采集的腹部投影数据进行了影像重建,对比了传统的FBP算法、TV最小化算法和本文提出的基于非线性压缩感知的算法在腹部影像重建中的效果,把对图像去噪和保存图像细节信息具有良好作用的非线性滤波操作引入了压缩感知的理论框架,有效地强化了压缩感知在图像重建领域的作用效果。通过实验分别验证了中值滤波、双边滤波、非局部均值滤波和非局部中值滤波在压缩感知算法中的作用效果。实验结果表明,新算法在CT影像重建任务中比传统算法在去除图像噪音、保存图像细节、刻画精确边缘方面具有明显优势。然而,重建效果会根据引入的非线性滤波种类的不同而有所差异,主观观察和客观评价指标都表明基于非局部中值滤波的压缩感知算法获得了最优的图像重建效果。新算法的运行需要多个变量参数的共同作用,尤其是引入非局部滤波的情况下,不同的参数组合作用出不同的重建效果,因此参数的设置与训练是本研究面临的挑战。制定能够依据不同重建任务而进行自适应设置的参数决策系统是下一步研究的方向。针对新方案运行耗时长的问题,课题组将结合频率滤波来提高算法的运行效率。本文所提出的基于非线性压缩感知的CT影像重建算法不仅对低剂量照射条件下的图像重建具有良好的应用效果,而且具有应用在稀疏角度或有限角度扫描的CT图像重建中的潜在价值。

