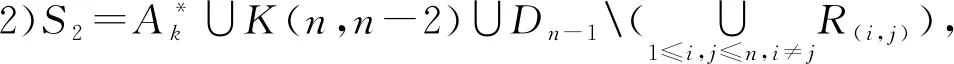半群的极大正则子半群
张心茹,罗永贵
(贵州师范大学 数学科学学院,贵州 贵阳 550025)
0 引言与准备
设S是半群,A是S的非空子集,∀a,e∈S,若e2=e,则称e是半群S的幂等元,A中所有幂等元之集记为E(A)。若存在b∈S使得aba=a,则称a是S的正则元,A中所有正则元之集记为Reg(A)。如果半群S中的每一个元素都是正则的,那么称S是正则半群。若存在b∈S使得a=aba,b=bab,则称b为a的逆元,a的所有逆元之集记为V(a)。易见,幂等元是正则元, 但正则元不一定是幂等元。设B⊆S是(正则)半群S的(正则)子半群,若B满足:对任意的α∈SB,有〈B∪{α}〉=S,则称B是半群S的极大(正则)子半群。
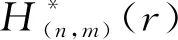
设Xn={1,2,…,n},Tn和Sn分别是Xn上的全变换半群和对称群,记Singn=Tn

Aiα=ai,1≤i≤r。
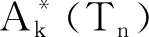
(α,β)∈L⟺im(α)=im(β);(α,β)∈R⟺ker(α)=ker(β);
(α,β)∈J⟺|im(α)|=|im(β)|
易见L⊆J,R⊆J,D=J,H=L∩R。记

我们用符号

表示Dn-1中满足下列条件的幂等元:

设n≥3,3≤k≤n,记
令E(Dn-1)为Dn-1中所有幂等元之集,于是有E(Dn-1)=E*∪E▽∪E△*且E*,E▽,EΔ*两两相交为空集。
对任意i,j,q∈Xn,做如下定义:
R(i,j)={α∈Dn-1:iα=jα}
Lq={α∈Dn-1:im(α)=Xnq}}


S1=G∪Singn
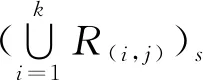
文中未定义的符号及术语参见文献[13-14]。
1 主要结果及证明
为完成定理1的证明给出以下若干引理。
引理1[5]设x,y是完全0-单半群中2个非幂等元,则xy≠0当且仅当Lx∩Ry含有幂等元,此时xy∈Lx∩Ry。
引理2[10]设1≤r≤n-1,则K(n,r)=〈E(Dr)〉且K(n,r)是正则子半群。
引理3[14]设S是半群,对任意的a∈S,则Ha中至多含有1个幂等元,若Ha中含有幂等元,则Ha是群。
引理4[14]设D是半群S的正则D-类a,b∈D,则H-类Hb包含a的逆元当且仅当H-类Ra∩Lb或Rb∩La包含幂等元。
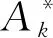

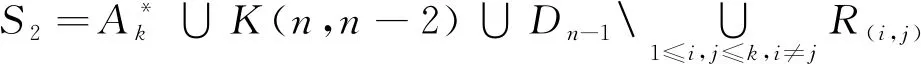

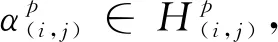

情形1 若α∈K(n,n-2),显然存在β∈K(n,n-2)使得αβα=α,则由正则性的定义知K(n,n-2)是正则的。
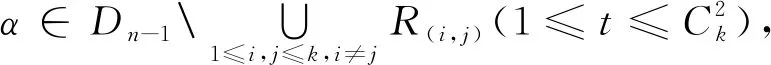


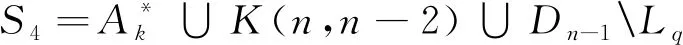

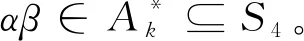
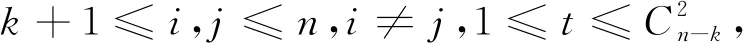

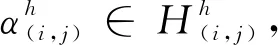
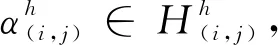

定理1的证明:
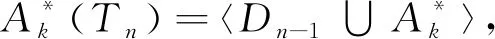
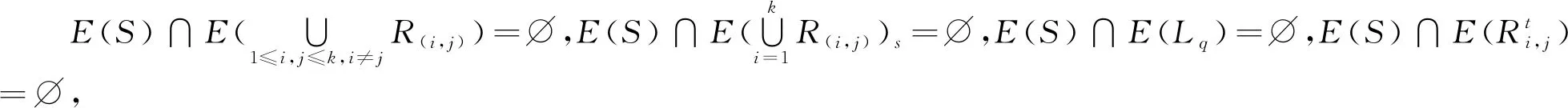
其次,证E(Dn-1)⊆E(S)。假设E(Dn-1)E(S)≠∅,任取e∈E(Dn-1)E(S)⊆Dn-1,则S∩Le≠∅且S∩Re≠∅,于是由S是正则半群可知,Le∩E(S)≠∅且Re∩E(S)≠∅,从而存在a,b∈E(S)使得a∈Le∩E(S),b∈Re∩E(S)且a≠b。由引理1知,ab∈S∩Ra∩Lb(因为e∈E(Dn-1)且ab∈Re∩Le=Ra∩Lb)。注意到a,b∈E(S),a,b∈S,aRabLe。再由引理4可得,存在ab的逆元c使得c∈S∩La∩Rb=S∩Le∩Re,于是c是群He中的元,从而存在自然数n使得e=cn∈S与e∈E(Dn-1)E(S)矛盾。因此E(Dn-1)⊆E(S)⊆S。

1)S1=G∪Singn