第二类曲面积分的计算方法与技巧——基于天津市大学数学竞赛试题的分析

郭阁阳

（天津职业技术师范大学理学院，天津300222）

第二类曲面积分是高等数学微积分教学中的一个重点，也是一个难点，其物理意义抽象难以理解，计算方法多变，计算技巧多样，相关数学知识面涉及较广，对大多数学生来说，掌握起来有一定难度。此外，由于各学校学生基础不同，教学要求也不同，一些学校只学习了第二类曲面积分的一些最基本的计算方法[1-3]，如直接积分法、Gauss公式、两类曲面积分之间关系转换法，导致学生无法应对一些计算复杂、计算量大、需要转化技巧的积分题目，导致恐惧心理。本文以天津市大学数学竞赛试题为例，结合十多年竞赛辅导经验，通过对竞赛试题的深入分析，在第二类曲面积分常规计算方法的基础上，给出一些重要的计算技巧。这些计算方法和重要技巧的结合使用，使得第二类曲面积分的被积函数便于简化，实现积分简单计算。同时，对每种方法和技巧的解题思路和适用条件做了充分说明，以帮助学生加深理解，加强对基本解题方法与技巧的掌握。

1 第二类曲面积分的计算方法

1.1 直接积分法

第二类曲面积分的直接积分法是指将曲面积分化为二重积分进行计算，这是计算第二类曲面积分的最基本方法[4-6]。基本原则的通俗表达就是“一求”“二代”“三定域”（有时也被称为“一投”“二代”“三定号”）。以计算积分为例。“一求”是指根据曲面所给定的侧求出“±”号，特别有前侧、右侧、上侧为“+”；有后侧、下侧、左侧为“-”[7]。“二代”是指将曲面方程代入被积函数，即将曲面方程z=z（x，y）代入被积函数R（x，y，z）中替换掉z，得R（x，y，z（x，y））。“三定域”是指将曲面向指定坐标面投影，得到投影区域Dxy，进而得到

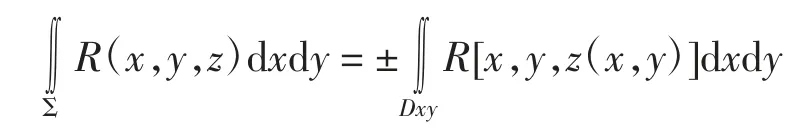
关于直接积分法的两点说明：

（2）注意多值问题的处理。多值问题是指曲面向某坐标面投影时，曲面是2个曲面，如单位球面在第一、五卦限的部分曲面，当向xoy平面作投影时，曲面就分为第一卦限部分和第五卦限部分对于多值问题，若采用直接积分法硬算，计算量很大，且有很多重复计算，所以一般可采用奇偶对称性技巧简化计算。

1.2 Gauss公式

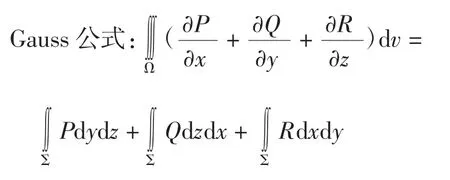
关于使用Gauss公式的几点说明：

（1）方向性问题。外侧为正，内侧为负。

（2）是否封闭问题。若不封闭，则需要补面，使之封闭。

（3）有无奇点问题。若Ω内含有使得P、Q、R一阶导不存在的点，需要补面抠除该点。

（4）Gauss公式的适用性问题。Gauss公式并不适用于所有的第二类曲面积分，一般要求积分域规则，且很简单，否则不能使用Gauss公式。

1.3 类型转换法

化第二类曲面积分为第一类曲面积分[8-9]

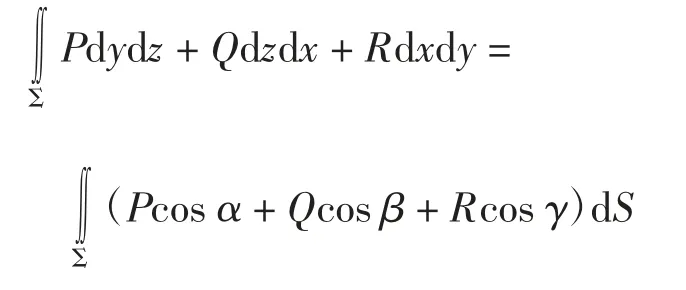
关于类型转化法的两点说明：

（1）该方法非常适用于被积函数P、Q、R中含有抽象函数的题目。

（2）若对于第二类曲面积分的奇偶对称性和轮换对称性不了解的情况下，使用类型转化法，将第二类曲面积分化为第一类曲面积分，进而使用一类曲面积分的奇偶对称性和轮换对称性技巧，可简化计算。

1.4 投影转换法

投影转换是指由dydz=cosads，dydz=cosβds，dydz=cosγds，得

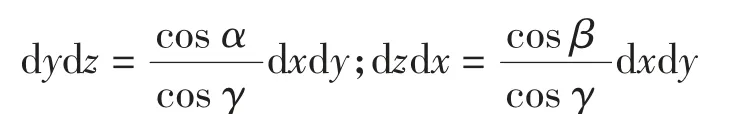
从而

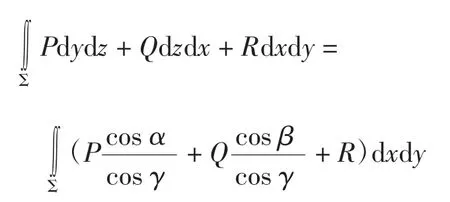
关于投影转化法的两点说明：

（1）对于被积函数P、Q、R都不恒为0的情况下，若用直接积分法，需算3个积分，过程较复杂，可使用投影转换法，只计算1个积分，便于计算。

（2）对被积函数P、Q、R中含有抽象函数的问题，使用该方法也可行。

1.5 参数方程法

则有

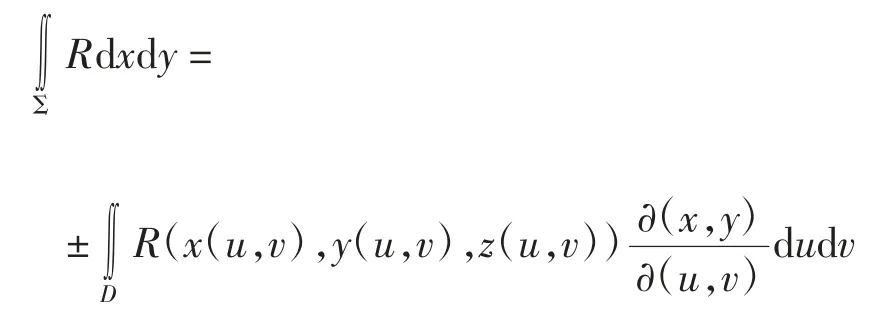
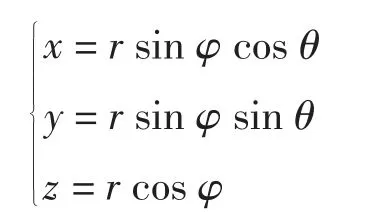
雅克比行列式为r2sinφ。

2 第二类曲面积分的计算技巧

2.1 代入性

第二类曲面积分的代入性是指积分曲面是由积分变量的等式给出的，可将曲面方程代入到被积函数中，以简化被积函数。

2.2 垂直性

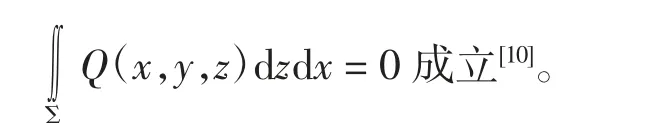
2.3 奇偶对称性

第二类曲面积分的奇偶对称性是指若曲面∑关于xoy面对称，当R（x，y，-z）=-R（x，y，z）时，

2.4 轮换对称性

第二类曲面积分的轮换对称性[10]是指：

（1）被积函数满足轮换对称性，即被积表达式中x，y，z的按轮换次序：x→y→z→x代换后，被积表达式不变。

（2）积分曲面及其指定侧也具有轮换对称性，这是指曲面在各坐标面上的投影区域相同，且所给的符号也相同。

这表明若被积表达式的变量互换位置，被积表达式不变，且区域的边界方程中的变量互换位置，区域也不变，则互换后积分值不变。

3 典型例题分析

本文通过对2道典型的天津市大学生数学竞赛试题的分析，结合前面给出的计算方法和重要技巧，给出试题的各种解法。

例1（2016年天津数学竞赛试题）计算，其中曲面1被平面z=0，x-y+z=2所截出部分的外侧。

解法 先利用可代入性将x2+y2=1代入积分，化简积分得

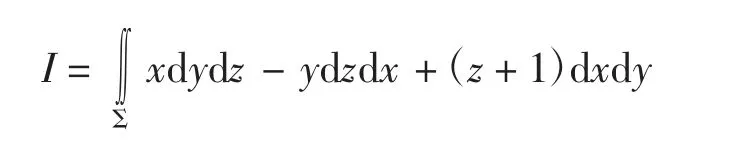
由Gauss公式得

其中，对积分I1应用Gauss公式计算三重积分得

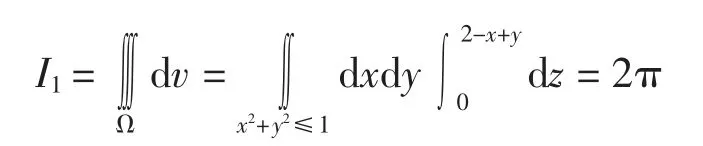
对积分I2应用垂直性得

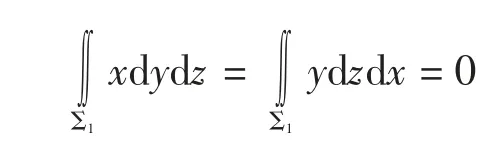
直接积分得

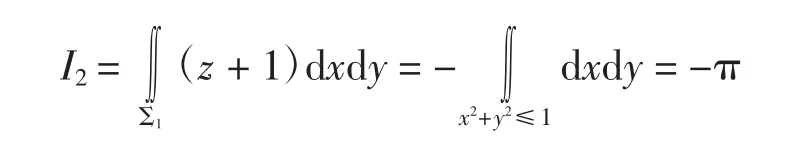
对积分I3应用投影转换法，其中∑2法向量为（1，-1，1），方向余弦为直接积分得

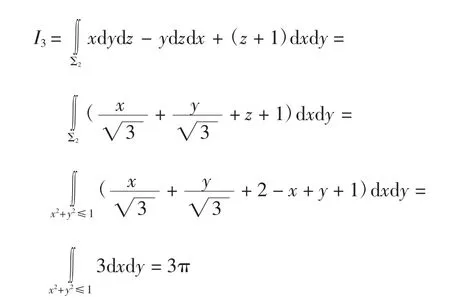
综上，得

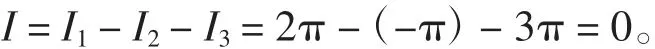
注1Gauss公式法是对第二类曲面积分的最常用方法，但本题需要补一个斜的平面，这是不多见的，随之产生的计算量也增加了很多，读者可将本题作为一个典型题目。

注2整个解题过程利用到了第二类曲面积分的可代入性、垂直性、Gauss补面、投影转换法、二重积分奇偶对称性技巧。

例2（2015年天津数学竞赛试题）计算曲面积分，其中z2=1外侧。

分析 一般第二类曲面积分，先考察Gauss公式，从Gauss公式使用的4点注意上看，虽然外侧、封闭没有问题，但有奇点且无法抠除，同时易见第4条，很复杂，不便于计算，故不能直接使用Gauss公式。这时，可考虑用各种技巧化简积分，进而再用直接积分法。

解法1观察球面∑：x2+y2+z2=1及被积函数，该二类曲面积分具有轮换对称性，即

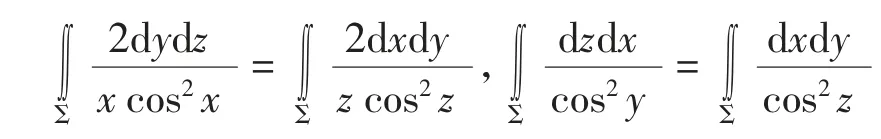
从而

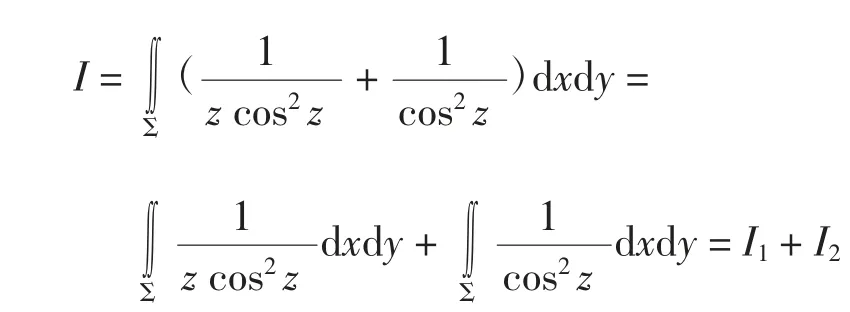
由第二类曲面积分的奇偶对称性得

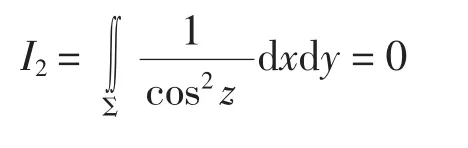
下面计算I1，由于第二类曲面积分是多值问题，取可用奇偶对称性处理，得到积分

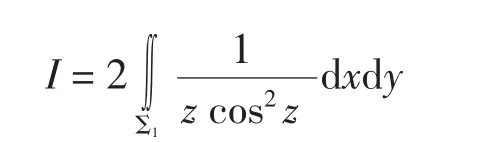
进而，利用第二类曲面积分的直接积分法可得

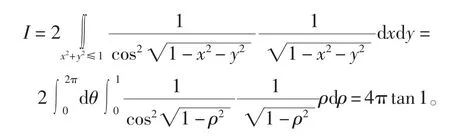
注1该解法需要对第二类曲面积分的奇偶对称性和轮换对称性有较深的理解和熟练计算的能力，一般课堂上对该知识点很少介绍和讲解，更多见于数学竞赛试题或考研试题中。

注2整个解题过程利用到了第二类曲面积分的轮换对称性、奇偶对称性、第二类曲面积分的多值问题以及直接积分法。

解法2利用类型转换法，化第二类曲面积分为第一类曲面积分。曲面∑的法向量为（cosα，cosβ，cosγ）=（x，y，z），进而得

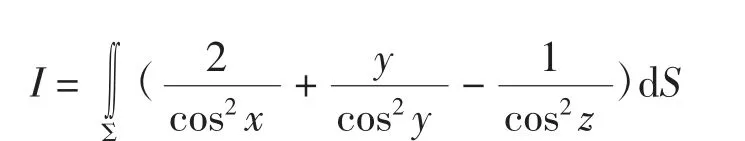
由第一类曲面积分的奇偶对称性得

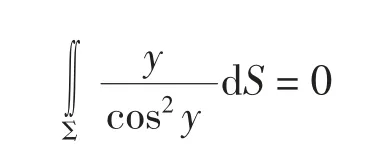
由轮换对称性得

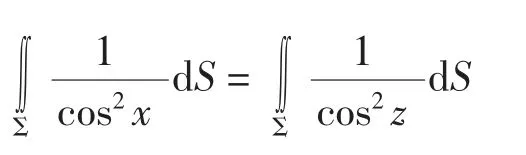
故

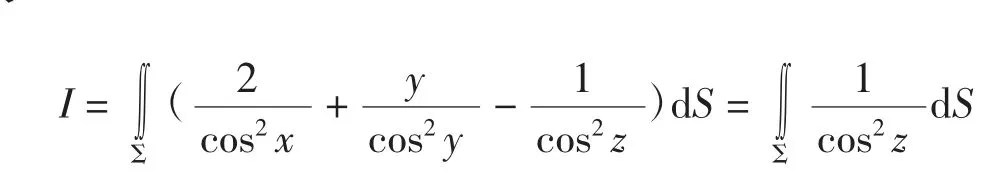
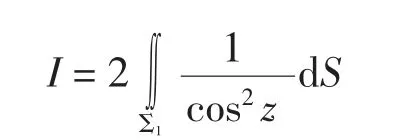
进而，利用一类曲面的直接积分法可得

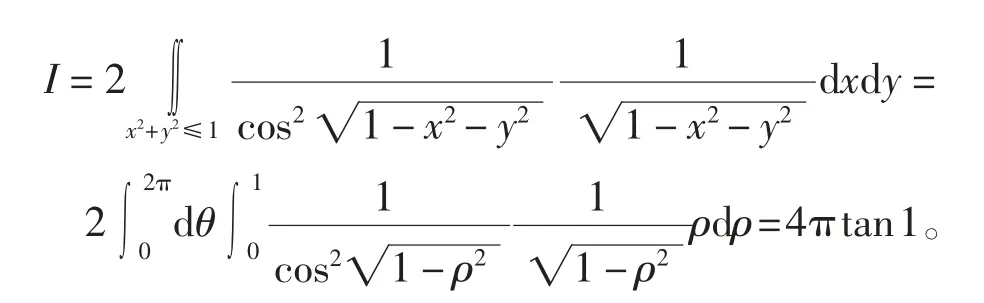
注1该解法充分利用了学生对第一类曲面积分的奇偶对称性和轮换对称性较深的理解和熟练的计算，利用类型转化法转到第一类曲面积分问题，进而求解。

注2整个解题过程利用到了类型转化法、第一类曲面积分的奇偶对称性、第一类曲面积分的轮换对称性、第一类曲面积分的多值问题，以及一类曲面积分直接积分法。

解法3球面参数方程法，解法2中最后一个积分的计算可以采用球面参数方程法。设球面的参数方程为

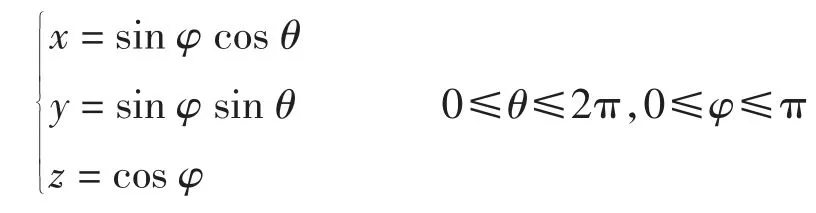
则

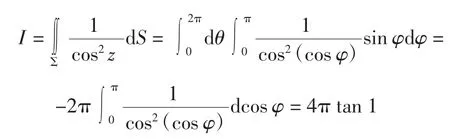
4 结语

本文通过一题多解，比较了每种解法的计算量和复杂性，可以看出计算方法和技巧选取的重要性。在计算第二类曲面积分时，应根据被积函数和积分曲面的特点，结合本文所给的计算方法和技巧的使用条件，选择恰当的方法和技巧，降低问题的复杂性，简化计算。理解第二类曲面积分的计算方法是基础，掌握第二类曲面积分的计算技巧是关键。对于学生来说，认真分析，究其本质，融会贯通，必定能起到事半功倍的效果。