简谐振动圆频率教学引入方法探讨

王金华

（天津职业技术师范大学理学院，天津300222）

圆（角）频率ω是大学物理中非常重要的概念，一般在讲授简谐振动这一知识点时引入。由于理工科公共基础课程的课时关系，教师无法对其深入讲解，在教学过程中，学生对圆频率的理解和接受存在许多困惑。同时，理工科专业《大学物理》教科书在引入圆频率时，大部分采用“定义”方式，即“定义”或“令ω=（以弹簧振子简谐振动为例）[1-9]”，直接称其为圆频率；同时部分参考书依据圆频率与频率间关系，将圆频率表示为2πs内完成振动的次数[10-11]。有些物理教学工作者对此提出异议，认为2π没有“s”的涵义[12]，因此，学生容易对圆频率这一概念产生不解和困惑。本文对理工科专业大学物理授课过程中圆（角）频率ω的引入方法进行探讨，提出基于学生“形象化”思维习惯，在讲授旋转矢量分析法时引入圆（角）频率ω概念，可以减少学生理解圆（角）频率ω时的困惑。

1 形象化理解圆频率ω的分析讨论

频率是单位时间内完成（事件）的次数。由于中学物理中讲授诸多物理原理和概念时，大多从日常生活中的现象入手，所以学生在理解物理概念和原理时有“形象化”思维惯性[13]。因此，学生在面对圆频率时，易简单、机械、形象化地将“圆频率”与“频率”建立直接联系，在脑海中寻找相关物理或几何图像。“圆频率”概念在“频率”前面冠以“圆”字，但是以弹簧振子为模型的振动方程讲授过程中不存在“圆”的信息或图像，此处引入“圆频率”概念，对于学生常按几何物体、物理图像、物理现象为知识基础和思维习惯的学习行为来讲，理解圆频率这一概念时就会产生诸如“为什么称之为圆频率，它与频率是否是同一概念，与圆有什么关系”等困惑。一般地，理工科常见参考书以讲授弹簧振子简谐振动为例，弹簧振子的振动如图1所示。

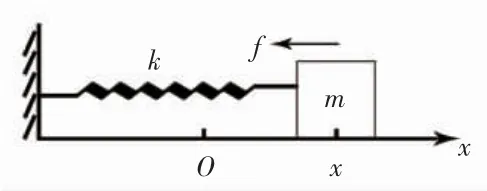
图1 弹簧振子的振动

一轻弹簧（质量忽略不计）劲度系数为k，左端固定，右端连一质量为m的物体，放在光滑水平面上，物体所受阻力忽略不计。物体位于O处时，弹簧具有自然长度。根据胡克定律与牛顿第二定律，有

求解方程（2），得到简谐运动方程

运动方程（3）为周期函数，其函数值随自变量变化周期性循环出现。因此，从x=A cosθ（t）的周期性来看，“频率”也与其函数值的周期性变化相关。

简谐运动方程x=A cosθ（t）中相位（相角）是极其重要的量，其不仅是该周期函数的自变量，反映周期函数在同一函数值下的不同时间或时间差，还包含了相位（相角）随时间变化的快慢。进一步求解，得到

与后续讲授的旋转矢量分析法相结合，旋转矢量分析法示意图如图2所示。

图2 旋转矢量分析法示意图

以上是基于学生形象化的思维习惯，结合大学物理旋转矢量分析法知识点，对弹簧振子简谐振动的动力学方程、运动方程、相位、相关函数关系的周期、频率、圆（角）频率等概念引入过程的重新解读，有助于理工科专业学生在学习大学物理时基于“形象化”思维习惯，进一步理解和掌握相关概念。但是，这种有益的理解方式并非真正的理解，而是为减少学习过程中暂时出现的困惑，毕竟对物理量、物理概念的理解和掌握要从物理学的发展历史、实验背景、数学处理方法等角度综合把握。

2 形象化思维习惯的圆频率ω授课引入方法

上述关于形象化理解“圆频率”的分析思路是基于熟练掌握圆频率所涉及微分方程、余弦函数周期、简谐振动振动特点、旋转矢量分析法等知识的前提下形成的，如把旋转矢量分析法与求解弹簧振子动力学微分方程合并讲解，进行“前后呼应”分析。此处的“前后呼应”是指利用旋转矢量法的几何图像，从“形象化”角度帮助区分或理解频率和圆频率，并非利用旋转矢量法定义圆频率。在大学物理实际教学过程中，由于授课顺序、学时的关系，无法按照上述思路对这一系列知识点进行整体讲授，因此参考书或课堂授课过程常出现直接“定义”或“令（以弹簧振子简谐振动为例）”，并称其为圆频率。该模式下讲授弹簧振子简谐振动并涉及圆频率时，由于受授课顺序、课时限制等原因影响，不能做到“及时呼应”，或前后呼应时间间隔太长（因课时关系，讲授弹簧振子简谐振动动力学方程、运动学方程、周期、频率等与旋转矢量分析法这一知识点存在课次间隔）。对于“圆频率”这一直接定义的物理量，学生容易对定义为圆频率、圆频率的本质等产生一系列疑惑。

基于学生的形象化思维习惯，以及授课顺序、课时限制等矛盾，建议可在授课过程中采用如下两种方案引入圆（角）频率ω：

3 结语

在物理学公式、原理、概念的学习过程中，学生常基于形象化思维习惯理解相关概念。简谐振动中圆频率概念，因没有“圆”形象，学生易对“频率”和“圆频率”概念产生困惑。本文提出旨在减少学生理解困惑的引入方法或讲授圆频率的方法，考虑到授课顺序及学生形象化思维习惯，在求得x=A cosθ（t）运动方程后，不直接定义为圆频率；待讲授至旋转矢量分析法时，结合其“圆”形象特征及振幅矢量的旋转角速率，给出圆频率符号、概念数量关系等。利用这一方法讲授圆频率概念，有助于学生在“圆”形象基础上理解圆频率，避免理解频率、圆频率时产生混淆和困惑，达到提高课堂授课效果的目的。