双轴运动系统GPCC与交叉耦合轮廓控制对比研究

张秀云，王志强，卞 杰

（1.天津职业技术师范大学天津市信息传感与智能控制重点实验室，天津300222；2.天津职业技术师范大学汽车与交通学院，天津300222；3.云南工业技师学院，曲靖655300）

在多轴轮廓轨迹的跟踪控制中，提高轮廓精度、实现精密轮廓跟踪一直是运动控制领域研究的重点课题之一。在传统方法中，各轴的运动惯性、负载不平衡以及响应不及时等问题会造成轨迹转折点处轮廓误差大、动态响应速度慢的问题[1]，通常可以通过降低单轴的跟踪误差来提高轮廓精度，近年来已有很多学者通过设计更高精度的单轴控制器来提升系统轮廓性能，如采用前馈控制[2]、零相位误差跟踪控制[3]等。但是仅仅提高单轴跟踪精度不能完全保证多轴轮廓误差的降低[4]，为此需要同时协同多轴控制，Koren[5]最早提出交叉耦合轮廓控制（cross-coupling contour control，CCCC）以提高双轴运动系统的轮廓精度，随后许多学者结合变增益控制[6]、鲁棒控制[7]、自适应控制[8]、滑模变结构控制[9]、迭代学习控制[10]、预测控制[11]以及模糊控制[12]等设计控制器，改善双轴运动系统的轮廓性能。广义预测控制（generalized predictive control，GPC）是Clarke等[13]于1987年提出的一种自适应模型预测控制算法，该算法被广泛应用于电机控制中。文献[14-15]将显式广义预测控制用于三相永磁同步电机的速度和位置控制，并设计单积分和双积分的预测算法跟踪阶跃和斜坡参考信号。文献[16]提出基于广义预测控制和扩展状态观测器的永磁同步电机控制，通过对扰动量的补偿，提高鲁棒性。

本文基于统一建模的思想建立统一预测模型，通过多步预测、滚动优化和反馈校正的方法对双轴运动系统的轮廓精度进行优化。

1 双轴运动系统轮廓误差及交叉耦合轮廓控制

本文所选用的双轴运动系统如图1所示。

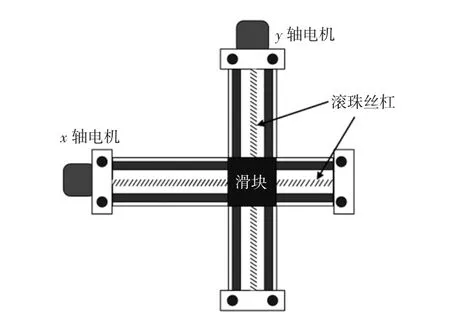
图1 双轴运动系统

伺服轴的实际位置P与电机机械角位置θ之间的关系为

式中：r为滚珠丝杠的螺距。

跟踪误差e和线性轮廓误差ε的计算方法为

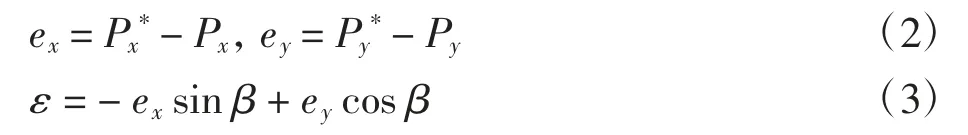
式中：β为轮廓轨迹期望位置点处的切线与x轴正方向的夹角。

传统交叉耦合轮廓控制策略简称为级联CCCC策略，该控制策略结构框图如图2所示。

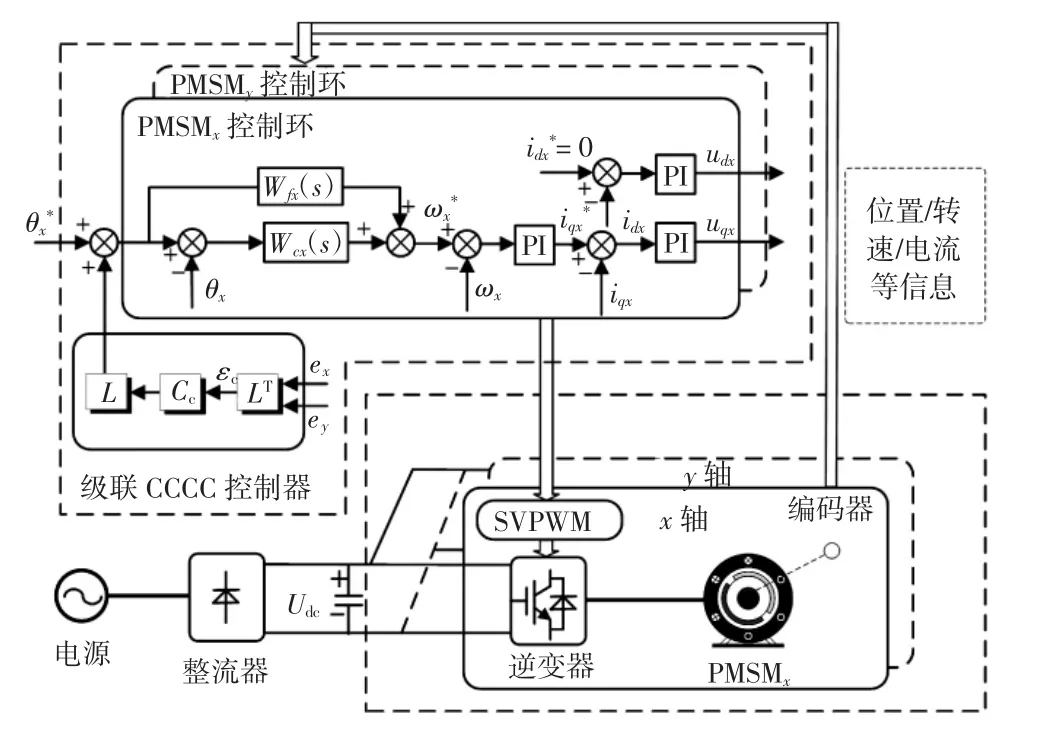
图2 传统交叉耦合控制结构图

从图2可以看出，传统交叉耦合轮廓控制结构具有一定局限性：①控制结构冗余，控制器参数调节繁琐。②采用经典级联型控制结构，多控制环极大地限制了系统的动态响应速度，存在轨迹转折点处动态响应速度慢、轮廓误差大等问题。

2 双轴运动系统广义预测轮廓控制

为了解决传统级联CCCC结构的局限性，本文区别于传统的“级联”控制结构，基于统一建模的思想，建立整合型同步控制架构，并设计紧凑的预测轮廓控制器，其控制系统结构如图3所示。

从图3可以看出，应用预测控制建立紧凑的预测轮廓控制器，能够实现轮廓误差的预测控制，且具有建模直观、结构简单等优点。

2.1 永磁同步电机的数学模型

PMSM的动态方程和运动方程为

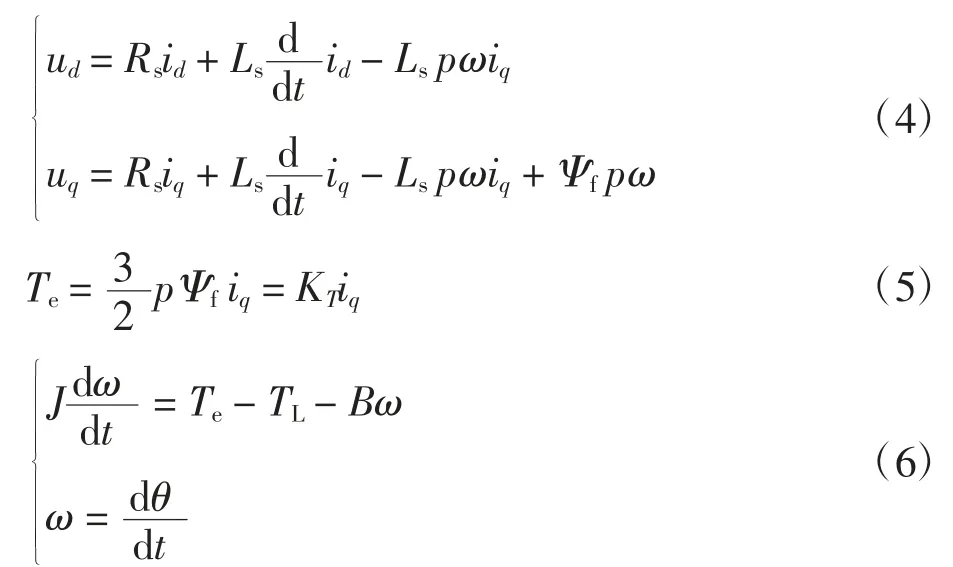
式中：ud、uq分别为d轴、q轴电压；id、iq分别为d轴、q轴电流；Rs为定子电阻；Ls为定子电感；ω为电机转子机械角速度；p为极对数；ψf为永磁体磁链；Te为电磁转矩；KT为转矩系数；J为转动惯量；B为摩擦系数；TL为负载转矩。

式（6）可以表示为关于θ的二次函数，即

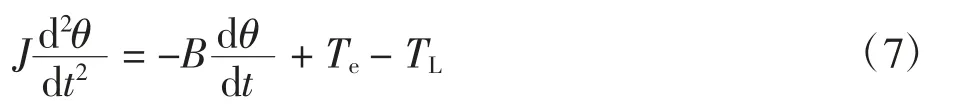
当电机空载即TL=0，由式（7）和式（5）可得PMSM机械运动开环传递函数为

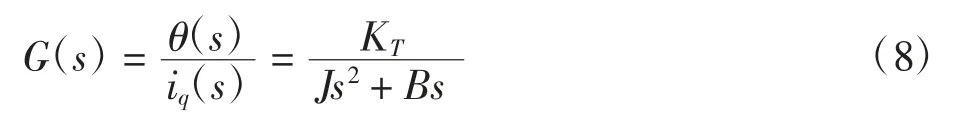
针对式（8），加入零阶保持器，并进行z变换，得到PMSM机械运动z域传递函数为

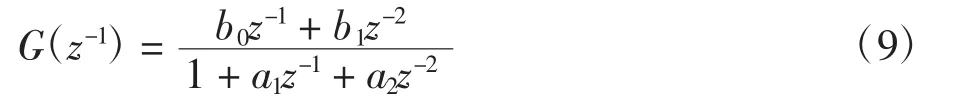
式中：a1=-（1+e-Ts·B/J）；a2=e-Ts·B/J；b0=（KT/B）·[Ts-（J/B）·（1-e-Ts·B/J）]；b1=（KT/B）·[（J/B）·（1-e-Ts·B/J）-Ts·e-Ts·B/J]；Ts为采样周期。

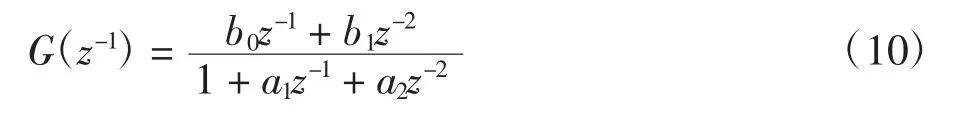
考虑随机扰动，可得到单轴PMSM的受控自回归积分滑动平均（CARIMA）模型为

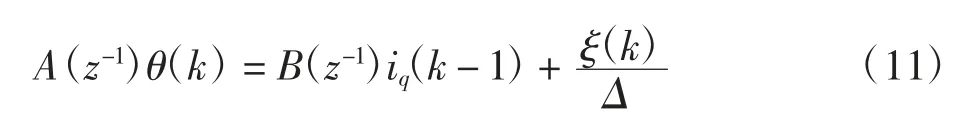
式中：ξ（k）表示随机扰动；Δ=1-z-1为差分算子；A（z-1）=1+a1z-1+a2z-2；B（z-1）=b0+b1z-1。

故双轴运动系统CARIMA模型可以表示为

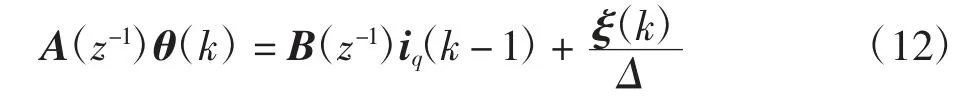
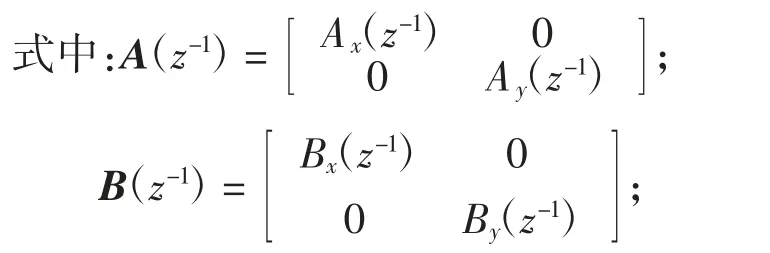
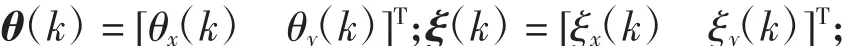
iq（k-1）=[iqx（k-1） iqy（k-1）]T；T表示转置。

2.2 双轴运动系统广义预测轮廓控制算法

本文基于统一建模的思想，采用GPC设计x、y轴整体位置-电流多步预测控制器，得到输出位置的预测序列，将预测序列与设定序列比较，得到跟踪误差与轮廓误差序列，将轮廓误差作为该双轴运动系统的内部变量，加入价值函数，通过最优化价值函数，确定作用于当前时刻的电流控制量，电流环采用id*=0控制，将其简称为GPCC策略，控制系统结构图如图4所示。

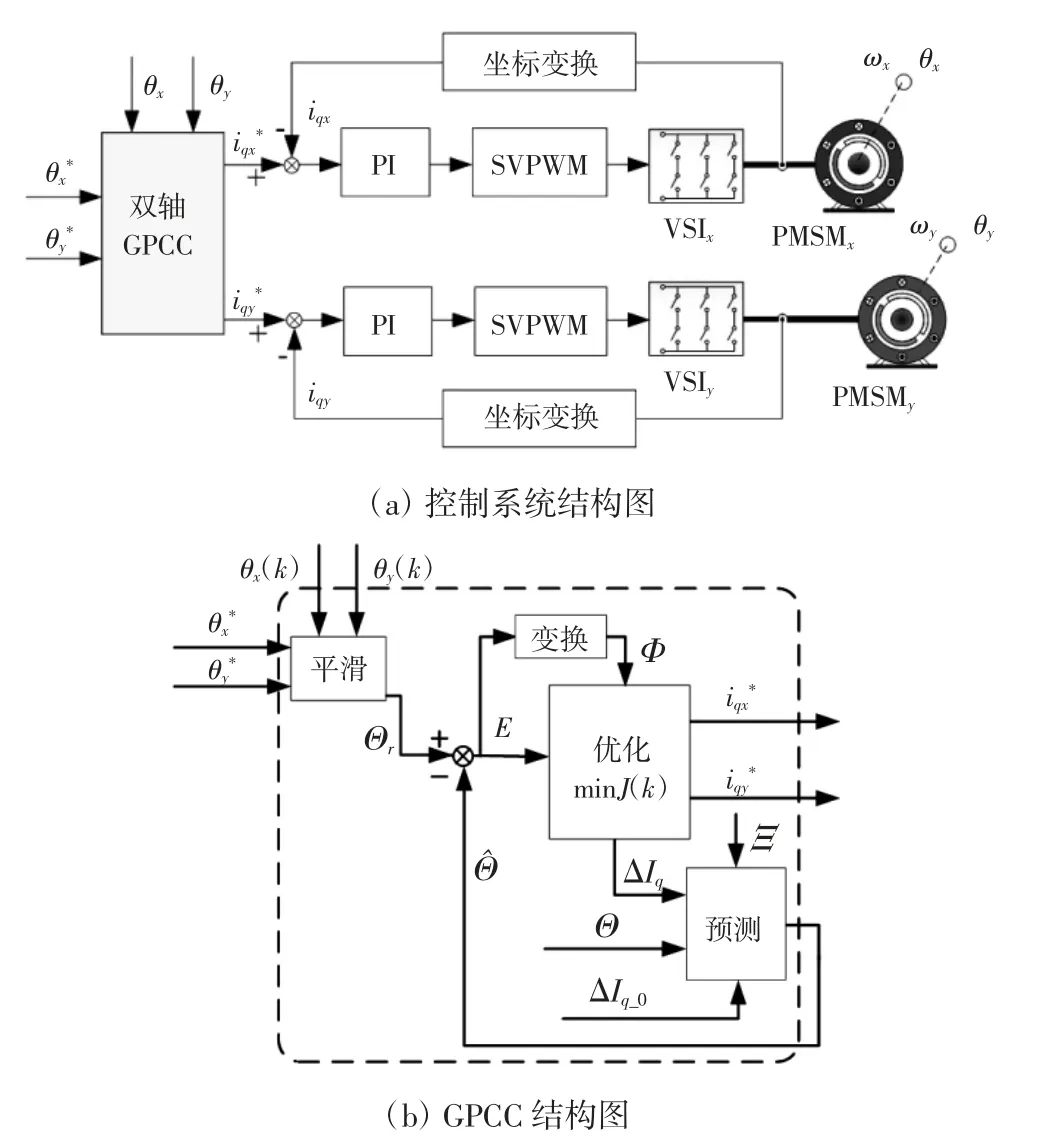
图4 GPCC控制系统结构图

图中θx*、θy*为x、y轴电机的未来位置设定值；θx（k）、θy（k）为x、y轴电机当前时刻的位置反馈值。在当前采样时刻kTs，基于统一预测模型，利用当前和未来Nu步的控制增量序列ΔIqT=[ΔIqxΔIqy]、过去的控制增量序列ΔIq_0T=[ΔIqx_0ΔIqy_0]以及当前和过去的系统输出ΘT=[ΘxΘy]，对x、y轴电机未来有限时域[（k+1）·Ts，（k+N）Ts]的输出序列进行预测，将得到的预测序列与经平滑后的位置设定序列ΘrT=[ΘrxΘry]进行比较，得到x、y轴电机的跟踪误差序列ET=[ExEy]，经过变换得到系统的轮廓误差序列Φ，将E和Φ加入价值函数，通过对min J（k）进行最优化处理，得到x、y轴电机当前时刻的控制量iqx*和iqy*。

（1）平滑

参考轨迹为一阶滞后模型，有

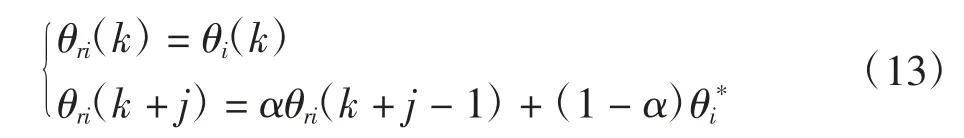
式中：0≤α＜1，α被称为柔化因子；j=1，…，N。

（2）优化

价值函数选为

式中：μ为轮廓误差系数；λ为控制加权系数。

（3）统一预测模型建立

若令N为预测域，Nu为控制域，nax和nay分别为Ax（z－1）和Ay（z－1）的最高阶次，nbx和nby分别为Bx（z－1）和By（z－1）的最高阶次，则可将x、y轴电机位置设定序列，预测序列和跟踪误差序列Θrx、Θry、Θ^x、Θ^y，Ex和Ey用统一符号Y表示，则有Y=[y（k+1），…，y（k+N）]；随机扰动序列为ζ=[ξ（k），…，ξ（k+N）]；轮廓误差序列为Φ=[ε（k），…，ε（k+N）]；x、y轴电机的当前、未来和过去时刻的控制增量序列分别为ΔIqx=[ΔIqx（k），…，Δiqx（k+Nu－1）]；ΔIqy=[Δiqy（k），…，Δiqy（k+Nu－1）]；ΔIqx_0=[Δiqx_0（k－ 1），…，Δiqx_0（k -nbx）]；ΔIqy_0=[Δiqy_0（k－1），…，Δiqy_0（k-nby）]；当前和过去的位置输出序列分别为Θx=[θx（k），...，θx（k-nax）]；Θy=[θy（k），…，θy（k-nay）]。

为得到j步后输出θ^（k+j）的最优预测值，使用Diophantine方程，即

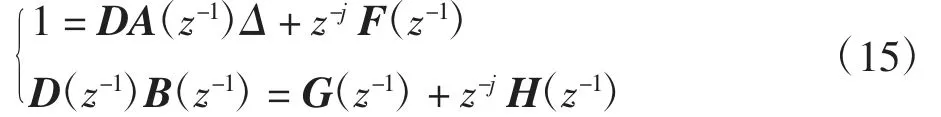
由已知的2台电机Ax（z－1）、Ay（z－1）、Bx（z－1）和By（z－1），根据Diophantine方程参数的递推公式可以得到x、y轴电机控制过程变量，分别为Dx、Fx、Gx、Hx和Dy、Fy、Gy、Hy，且D=diag[Dx，Dy]；F=diag[Fx，Fy]；G=diag[Gx，Gy]；H=diag[Hx，Hy]；其中

因此N步最优输出预测值为

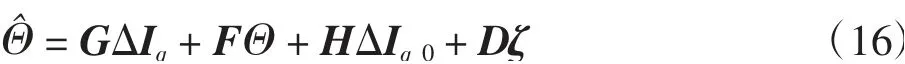
将式（16）代入式（15），可得

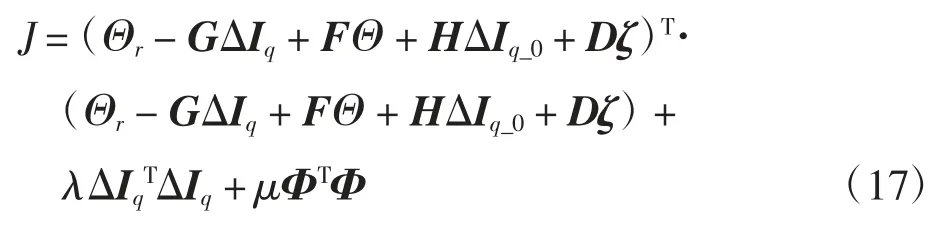
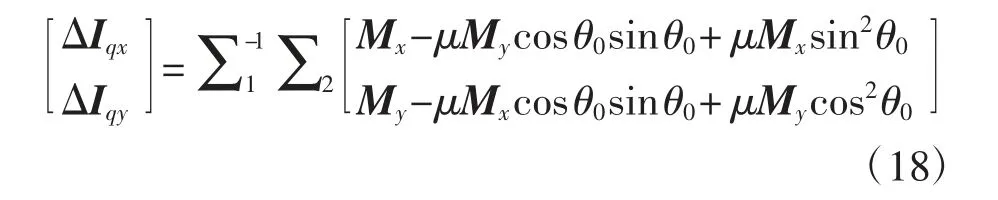
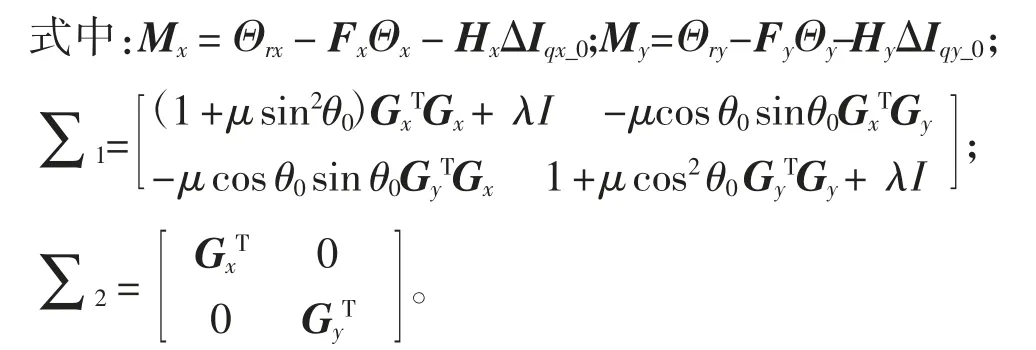
当前时刻广义预测控制量为

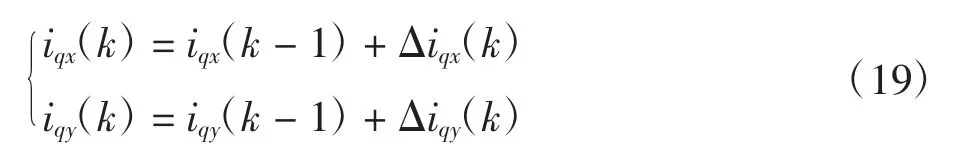
3 双轴运动系统GPCC性能分析

情况1：当μ=0，即价值函数不含轮廓误差项时，代入式（18），可得

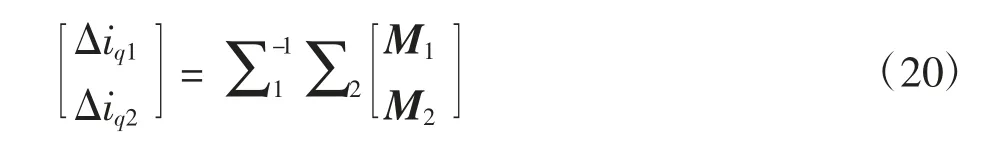
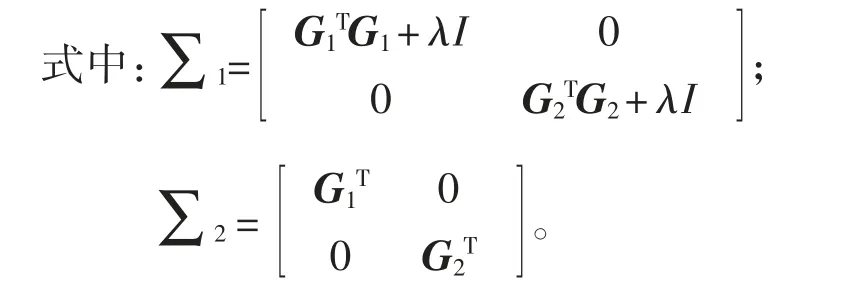
在这种情况下，为获得令人满意的同步性能，双轴在动态和静态下应该完全同步。

情况2：当Ax（z-1）=Ay（z-1），Bx（z-1）=By（z-1）且λ=0时，Gx（z-1）=Gy（z-1），代入式（18），可得

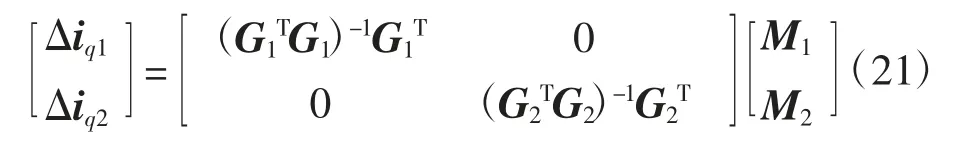
可以看出，当λ=0时，即价值函数中不含控制增量项，通过计算可以得到控制量与μ无关，但是为获得稳定及光滑的系统反馈，在大多数控制输入计算中，通常选λ>0。

4 仿真研究与分析

为验证所提出的GPCC策略对双轴运动系统的控制效果，通过Matlab的Simulink模块对双永磁同步电机系统进行仿真研究。

4.1 GPCC与CCCC算法对比

给定双轴运动系统折线运动轨迹，角度β为45°和-45°，x、y轴的进给速率均为10 mm/s，在0.1 s时，x轴电机加5 N负载，而y轴电机加3 N负载；在0.2 s时，x轴给定轨迹方向不变，y轴给定轨迹方向呈现90°弯折，即运动轨迹经过拐点，分别给出传统CCCC策略和所提出的GPCC策略下的轨迹、跟踪误差和轮廓误差的变化曲线，传统CCCC与GPCC下双轴运动系统输出响应如图5所示。

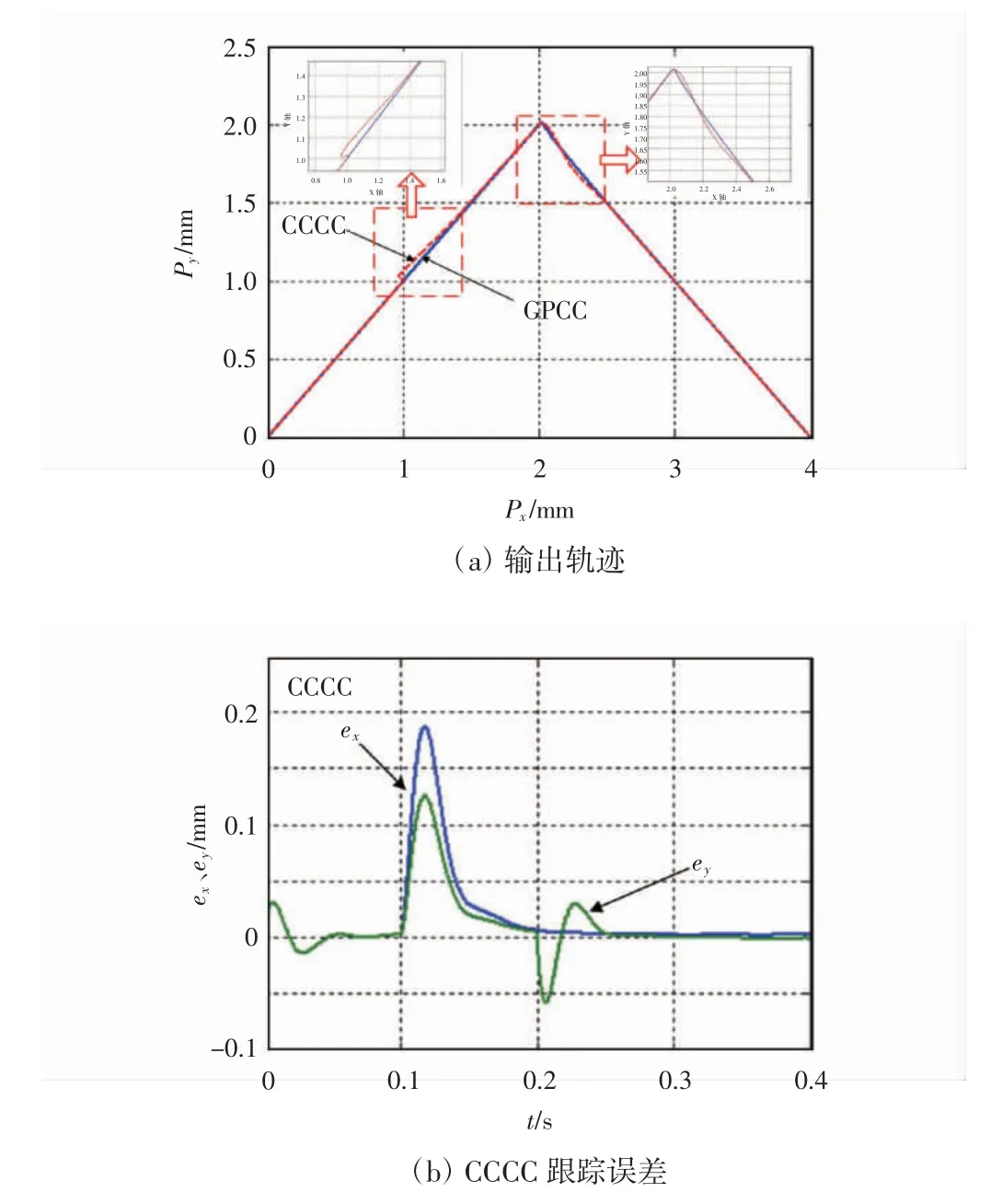
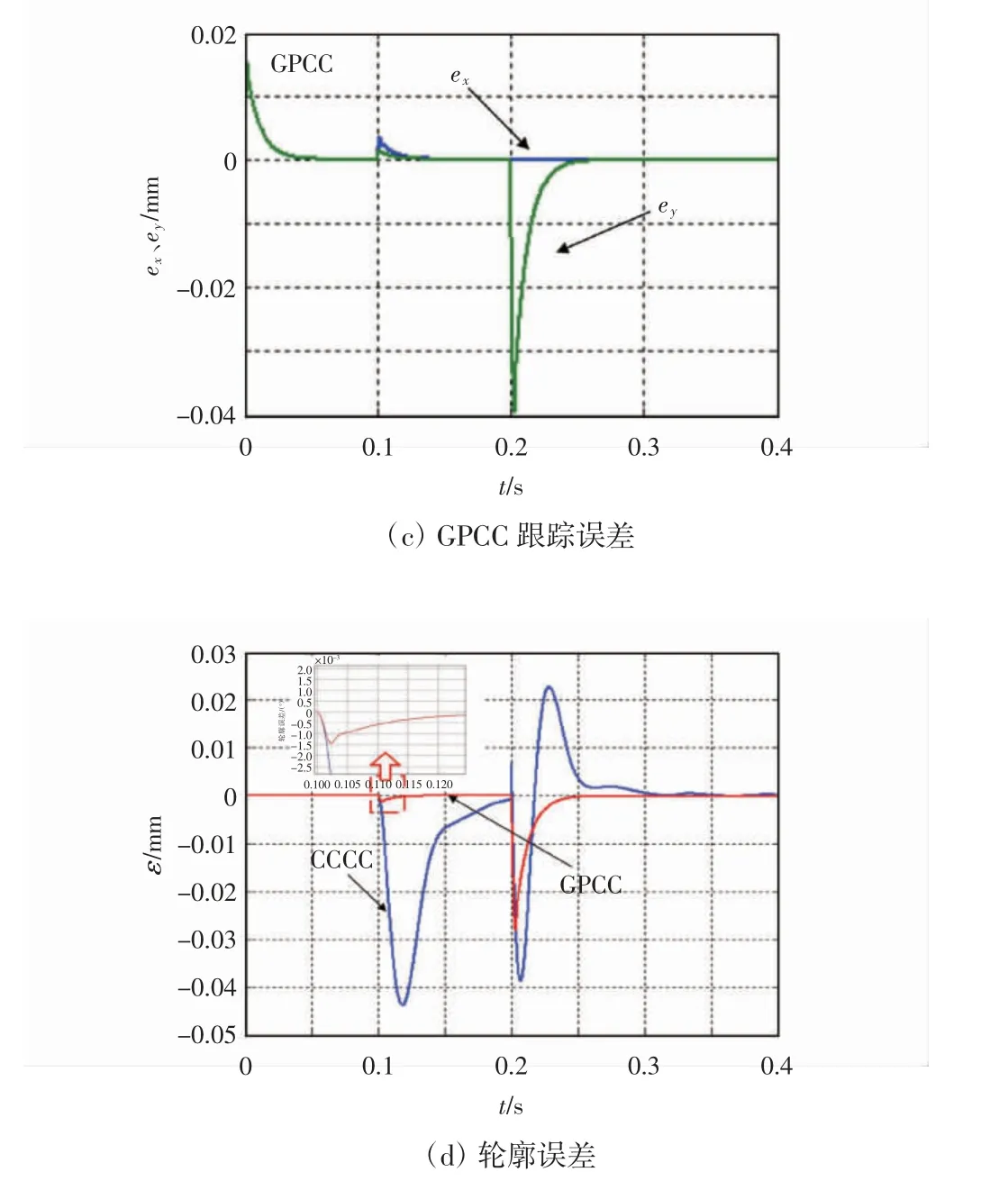
图5 传统CCCC与GPCC下双轴运动系统输出响应

由图5（a）可以看出，采用GPCC时轨迹的跟踪效果更好，特别是在电机运行过程中外加负载扰动时，位置信号跌落更小，且更快地恢复到给定值。由图5（b）和（c）可以看出，在加载和拐点时，采用GPCC时超调量更小，响应速度变快，即误差能更快速地收敛，具有更好的动态特性。由图5（d）可以看出，在加载和拐点时，采用GPCC时轮廓误差更小，且能够更快速地收敛，动态性能更好。

4.2 GPCC（μ=0）和GPCC（μ=2）对比

为了更好地验证轮廓误差项对于所提出的双轴运动系统GPCC策略的作用，将μ=0时与μ=2时两种情况相比较。给定与上述相同的双轴运动系统折线运动轨迹，图6为预测轮廓控制对应的轨迹、跟踪误差和轮廓误差的变化曲线。

由图6（a）可以看出，2种方法的跟踪性能没有明显差别。由图6（b）和（c）可以看出，在加载和拐点时，不含轮廓误差项的x轴跟踪误差在拐点时由于参考信号不变，跟踪误差曲线近乎一条直线，但是增加轮廓误差项时，x轴跟踪误差在拐点时会向y轴跟踪误差的方向倾倒，即牺牲一部分跟踪性能以提高同步性能，加载时情况亦是如此。由图6（d）可以看出，在加载和拐点时，采用改进算法时，轮廓误差虽然幅值没有明显变小，但快速性提高，动态性能更好。

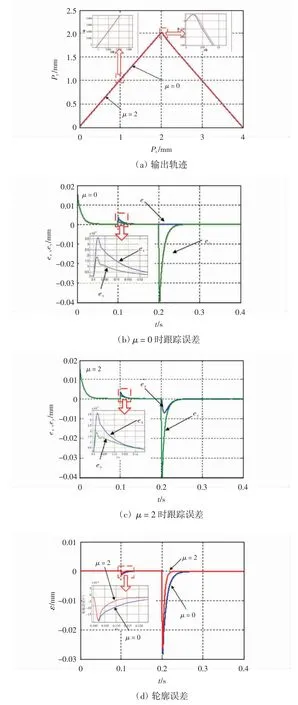
图6 GPCC(μ=0)与GPCC(μ=2)下双轴运动系统输出响应

4.3 轮廓误差系数对系统轮廓误差的影响

为了说明轮廓误差系数μ选取不同值时对轮廓误差的影响，给定与上述相同的双轴运动系统折线运动轨迹，图7为不同μ时的轮廓误差图。

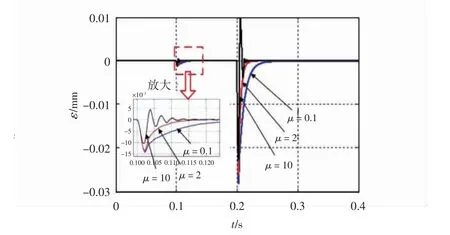
图7 不同μ时的轮廓误差图

从图7可以看出，当在加载或轨迹拐点时，μ=2比μ=0.1轮廓误差动态响应快，但当μ=10时，会出现振荡现象，这是因为当μ取很大的值时，相对来说跟踪效果的调节作用变弱，容易出现振荡现象。

5 结论

本文通过对比研究所提出的广义预测轮廓控制策略与交叉耦合轮廓控制策略，得到如下结论：

（1）本文所提算法基于统一建模的思想，将双轴运动系统中2台电机的位置环和速度环看作整体进行统一建模，能够简化双轴运动系统的整体控制结构，具有建模直观的优点。

（2）本文所提算法能够在保证稳态轮廓跟踪性能的前提下，提高系统瞬态轮廓跟踪性能，特别是在发生大转折时，轮廓误差会减小，且动态响应速度也会加快。

（3）本文所提算法易于拓展到三维运动轨迹，并且在多台电机的协同控制中也能够有较为广泛的应用。