绕丝结构砂轮磨削沟槽结构化表面*

唐成志， 吕玉山， 李兴山， 蒋坤良， 齐永超

(沈阳理工大学 机械工程学院， 沈阳 110159)

20世纪70年代，NASA的兰利中心发现鲨鱼皮表面的微沟槽结构可以减少8%～10%的阻力。这一发现不仅打破了“表面越光滑，摩擦阻力越小”的传统观点，而且证明了具有一定微结构的表面能够降低摩擦阻力[1-2]。

目前微沟槽结构的制造方法主要有滚压、金刚石飞切、电化学腐蚀、激光加工、磨削等。面对难加工材料和批量化生产时，磨削是高效的方法之一。为此国内外众多学者开展了磨削沟槽结构表面的研究。STEPIEN[3-5]首次在传统砂轮表面修整出螺旋沟槽，并在不锈钢工件表面磨削出宽约40 μm、深约20 μm的倾斜沟槽结构。DENKENA等[6-7]提出轮廓重叠修整的方法，利用此方法修整出的砂轮在汽轮机叶片上磨削出宽约40 μm、深度约为20 μm的沟槽结构，这种修整方法提高了磨削沟槽结构的效率。JEONG等[8]利用CAD研究了螺旋沟槽砂轮的磨削参数对沟槽倾斜角度的影响，并磨出倾斜角度在1.349°～9.931°范围内的沟槽结构。XIAO等[9]采用砂带磨削的方法在钛合金叶片上磨削出宽度为2.5～8.0 μm，高度为3.5～9.0 μm，顶角为28°～68°，截面为三角形的沟槽结构。CAO等[10]首先给出了不同修整率下的砂轮轴向和垂直方向的截面模型，其次提出了一系列微结构模型并研究了修整参数和磨削参数对结构形貌的影响，最后磨削出了宽度约120 μm的沟槽结构。XIE等[11]使用CNC技术将金刚石砂轮精密修整成V形，使用修整后的砂轮在单晶硅表面磨出宽约100 μm、深约70 μm的沟槽结构，在SiC和WC试件表面2次交叉磨削磨出高度达到173 μm和422 μm、深宽比约为0.87的微金字塔结构。GUO等[12]利用超声振动辅助磨削在WC和SiC上加工出边缘半径小于1 μm的V形沟槽。

以上学者在磨削微沟槽表面领域做出了很大贡献，然而精密修整砂轮形貌成本很高且砂轮易磨损。为解决这一问题，本文中提出了一种绕丝结构化砂轮磨削沟槽结构的方法，研究了沟槽结构的创成机理和磨削参数对沟槽形貌的影响。

1 丝锯砂轮模型

将丝锯紧密缠绕在基体上，建立的砂轮几何模型如图1所示。丝锯可以离散成无数圆形截面，每个圆截面上磨粒以母线中心点为原点呈圆周分布。假设砂轮基体半径为RS、丝锯半径为r、缠绕螺距为P0、丝锯截面在螺旋线上相位角为φ，则如下得到丝锯中心点位置方程：

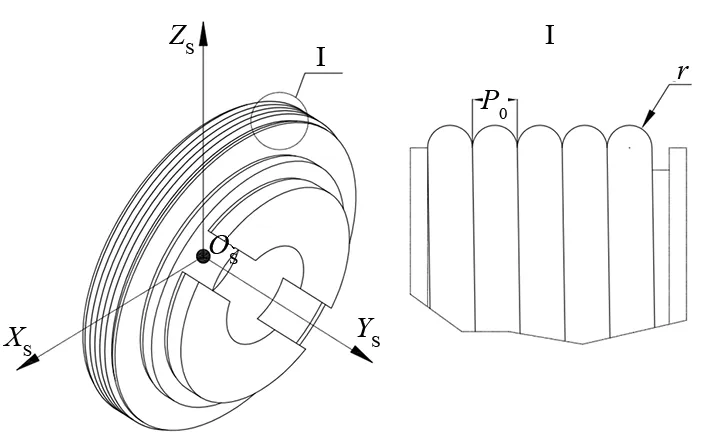
图1 丝锯砂轮几何模型

(1)

如图2以任一截面中心点O1(XSφ0,YSφ0,ZSφ0)即φ等于φ0点为中心点，与砂轮坐标轴Y平行方向为Y1轴，通过砂轮坐标系点(0,YSφ0,0)方向朝外为轴建立丝锯切向截面坐标系，以下标1以示区别。因为朝基体方向的磨粒是不参与切削的且丝锯螺旋角较小，所以将丝锯在坐标系上截面理想化为圆形且将上半圆弧分为J等份，则θ=π/J。

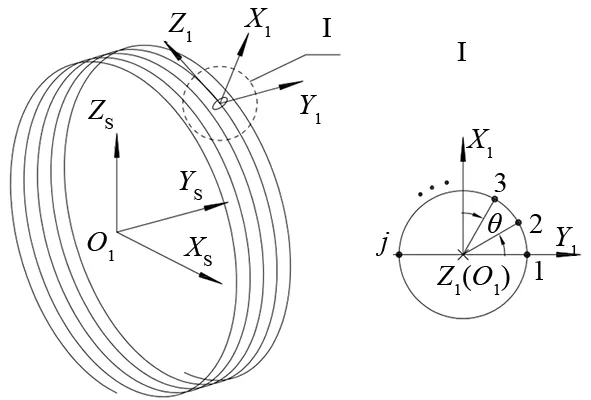
图2 丝锯截面与切削点分布

则理论每颗磨粒点在切向截面坐标系中坐标方程如下：

(2)

为了得到磨粒在砂轮坐标系上坐标，将切向截面坐标系旋转至与砂轮坐标系平行，得出第j个磨粒在旋转后的坐标如下：

(3)

将旋转后的坐标系平移变换至与砂轮坐标系重合，第j个磨粒点在砂轮坐标系中坐标如下：

(4)

将式(1)、(2)、(3)代入式(4)得到砂轮上每颗磨粒位置方程如下：

(5)

根据公式(5)只需知道丝锯截面φ角和磨粒在切向截面坐标系上θ角，就可以确定所有磨粒在砂轮上的位置。

2 磨粒切削运动轨迹方程

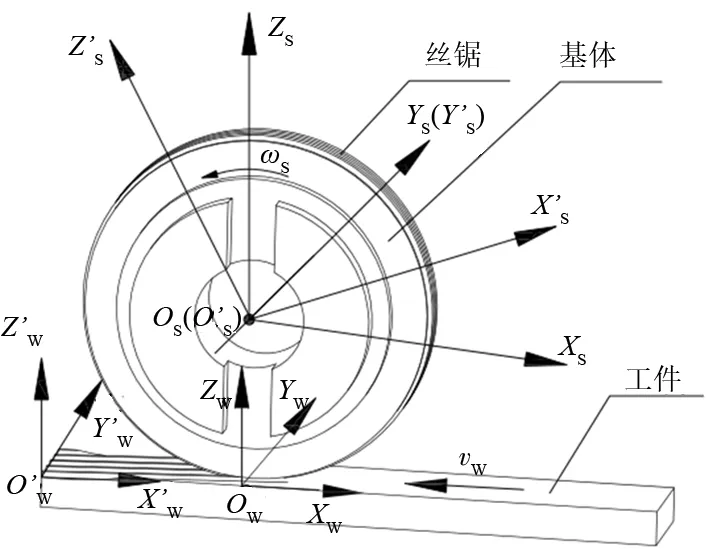
图3 磨削运动坐标示意图

磨粒时刻相对于工件的位置是建立切削轨迹的前提，即磨粒时刻在工件相对坐标系中的位置。坐标变换时，首先，砂轮只进行旋转运动所以坐标变换只与初始坐标和旋转的角度有关，转换方程如下：

(6)

其次，砂轮绝对坐标系与工件绝对坐标系仅在ZS方向存在距离，因此XS、YS坐标是没有变化，ZS方向的距离是RS+2r-ap，其中ap为磨削深度，转换方程如下：

(7)

最后，工件在磨削中在XW方向以vW速度进行线性移动，转换方程如下：

(8)

将式(6)、(7)代入式(8)得到转换方程：

(9)

3 沟槽结构创成机理

图4为截面a处砂轮截面轮廓示意图，截面轮廓磨粒突出高度呈正弦规律分布，式(10)为截面轮廓方程，并根据轴向分布规律得出砂轮其他位置截面轮廓方程如式(11)所示。

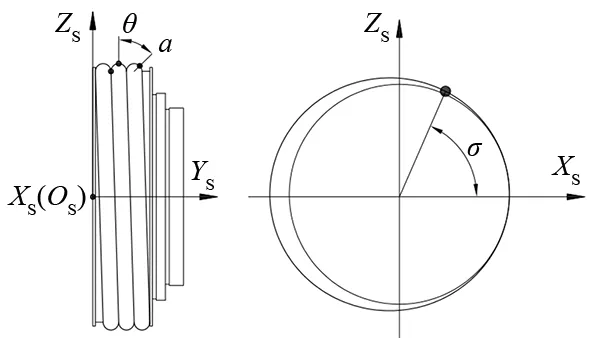
图4 砂轮轴向截面轮廓

(10)

(11)

式中：(XSa,ZSa)为磨粒在a上的坐标；

(XS2,ZS2)为磨粒在其他截面上的坐标；

σ为轮廓点与水平轴的角度；

θ为截面与截面a的角度，逆时针为正。

图5为单颗磨粒切削轨迹。图5中xen是磨粒切入点坐标，xex是磨粒切出点坐标。

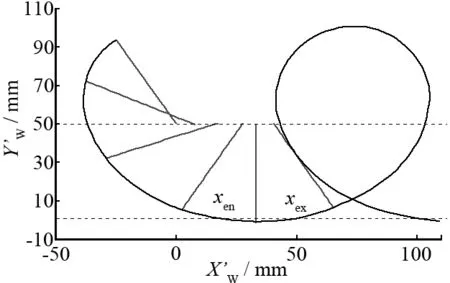
图5 单颗磨粒切削轨迹

图6为截面上单周期磨削轨迹：A、C点是截面切削工件临界磨粒；B点是截面最高磨粒；ξ是截面切削工件的磨粒所占圆心角；D是沟槽轨迹初始点；E是沟槽轨迹末点；l是截面单周期磨削总长度；红色线段为切入区域，蓝色线段为切除区域长度是截面磨削总长度的一半即l/2；lc是砂轮旋转1周工件进给长度，计算公式如下：

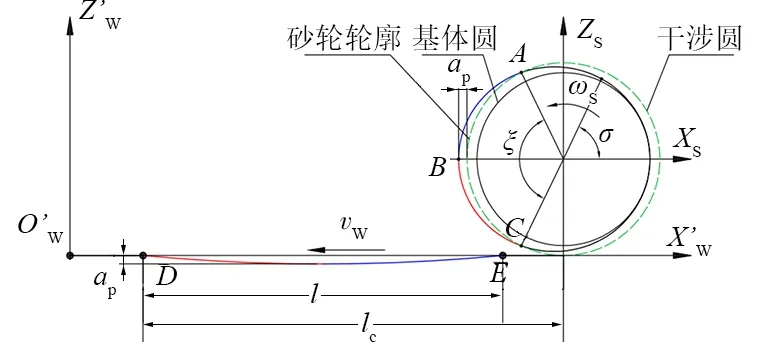
图6 截面上单周期磨削轨迹

lc=2π(RS+2r)v*

(12)

式中：v*为速度比，即vW/vs。

圆心角ξ的计算：

r-ap=rsin(σ/2)

(13)

求得(0，2π)中2个解分别为σ1、σ2，则ξ=σ2-σ1。

因磨粒接触弧长的存在与磨削参数的选择，沟槽结构初始点并非是由图6中C点磨粒切削形成。根据D、E点的横坐标即可知截面切削长度，因此根据式(6)建立砂轮截面磨粒运动轨迹方程如式(14)。

(14)

式中：(XS2,ZS2)为截面点任意时刻坐标；

δ为磨粒旋转角度。

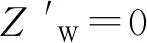
(15)

取N个砂轮截面以研究切削轨迹轴向分布，其结果如图7所示。

图7中β为沟槽倾斜角度，Δx为轨迹与1号轨迹进给方向偏距，Δy为轨迹与1号轨迹砂轮轴向偏距。因为砂轮所有截面形貌都相同，根据截面轴向分布规律和磨削运动可得所有截面磨削轨迹形状相同、长度相等均为l且互相平行；相邻轨迹在进给方向与轴向均有偏距。将所有切削轨迹的初始点与末点连接，最终形成与进给方向倾斜的沟槽。根据砂轮截面分布规律建立沟槽倾斜角度方程如下：

图7 切削轨迹轴向分布

tanβ=Δy/Δx=P0/lc

(16)

沟槽宽度方程如下：

w=lsinβ

(17)

沟槽间距方程如下：

S=lcsinβ

(18)

根据截面切削长度与筋条创成机理可以得出：当llc时，相邻筋条结构互相干涉，尖锐脊结构高度小于ap。磨削相离筋条时，增加砂轮速度时，l、lc变小而β变大，筋条宽度增大；增加进给速度时，l、lc变大而β变小，沟槽宽度变小；增加磨削深度时，则l变大而β、lc保持不变，沟槽宽度变大。

4 沟槽表面形貌仿真

4.1 仿真基本参数

根据所有磨粒的运动轨迹方程，利用MATLAB进行磨削沟槽表面的仿真。仿真参数设定为：砂轮基体直径为100 mm，丝锯母线直径为0.40 mm，磨粒直径为10 μm，砂轮转速分别为1 200 r/min(6.335 m/s)、1 800 r/min(9.503 m/s)、2 400 r/min(12.672 m/s)，工件进给速度分别为3、6、9 m/min，磨削深度分别为10、15、20 μm。

4.2 仿真结果与分析

4.2.1 进给速度对结构形貌的影响

图8是在砂轮转速为1 800 r/min、磨削深度为20 μm、不同工件进给速度下得到的沟槽形貌仿真图。从图8可以看出：当vW=3 m/min时，相邻沟槽干涉形成尖锐脊结构，这是因为砂轮截面切削长度l小于周期长度lc，沟槽宽度与间距相等约为417 μm，结构角度约为14.14°；当vW=6 m/min时，沟槽宽度约为316.4 μm，间距约为416.7 μm，结构角度约为7.18°；当vW=9 m/min时，沟槽宽度约为276.8 μm，间距约为418.5 μm，结构角度约为4.80°。分析得出：沟槽宽度随着进给速度的增加而减小；沟槽倾斜角度随着进给速度增加而减小；沟槽深宽比变化与宽度变化一致。

(a) vW=3 m/min

4.2.2 砂轮速度对结构形貌的影响

图9是在磨削深度为20 μm、工件进给速度为9 m/min、砂轮转速分别为1 200、1 800、2 400 r/min下得到的沟槽形貌仿真图。从图9中可以发现：当ns=1 200 r/min时，沟槽宽度约为210.8 μm，间距约为419.3 μm，结构角度约为3.20°；当ns=1 800 r/min时,沟槽宽度约为276.8 μm，间距约为418.5 μm，结构角度约为4.80°；当ns=2 400 r/min时，沟槽宽度约为336.9 μm，间距约为417.4 μm，结构角度约为6.39°。分析得出：沟槽宽度随着砂轮速度增加而增加；沟槽倾斜角度随着砂轮转速增加而增加；深宽比变化规律与宽度变化一致。

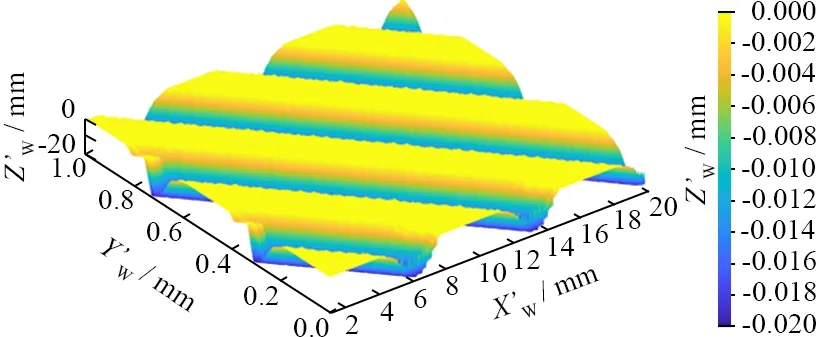
(a) ns=1 200 r/min

4.2.3 磨削深度对结构形貌的影响

图10是在砂轮转速为1 800 r/min、工件进给速度为9 m/s、不同磨削深度下得到的沟槽形貌仿真图。从图10中得出：当ap=10 μm时，沟槽宽度为211.3 μm，间距约为418.5 μm，结构角度约为4.8°；当ap=15 μm时，沟槽宽度约为274.6 μm，间距约为418.5 μm，沟槽倾斜角度约为4.80°；当ap=20 μm时，沟槽宽度约为281.8 μm，间距约为418.5 μm，结构角度约为4.80°。分析得出：沟槽宽度随着磨削深度增加而增加；沟槽倾斜角度不受磨削深度影响。

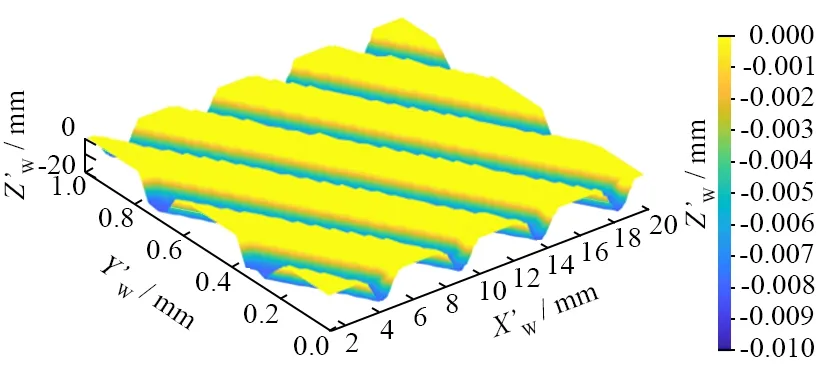
(a) ap=10 μm

5 结构化沟槽表面的实验验证

在砂轮基体上挂一层橡胶后进行缠绕丝锯，其中砂轮基体直径为60 mm，丝锯母线直径约为400 μm，金刚石微粉磨粒直径约为10 μm。

使用图11中的砂轮进行实验，实验参数设定为：砂轮转速分别为2 000 r/min、2 400 r/min、2 800 r/min，进给速度为9m/min，磨削深度为10 μm，得出的工件表面整体分布与局部放大如图12所示。

从图12中可以看出：当ns=2 000 r/min时，沟槽平均宽度为0.351 5 mm；当ns=2 400 r/min时，沟槽平均宽度为0.429 4 mm；当ns=2 800 r/min时，沟槽平均宽度为0.455 2 mm。由此可知沟槽的宽度随着砂轮转速的增加而增加，与仿真得出的规律一致。

(a) ns=2 000 r/min

图13为不同转速下的沟槽截面测量图。从图13中可以看出：在不同转速下的实际磨削深度只有5～6 μm，这是因为砂轮橡胶层发生了弹性变形；所有毛刺隆起高度只有1～2 μm；沟槽截面形貌为圆弧形与丝锯截面形貌一致。

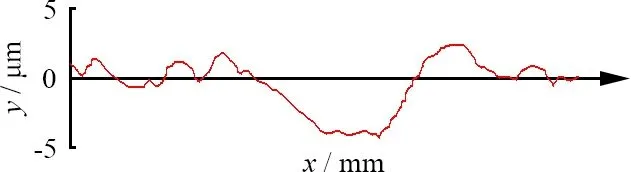
(a) ns=2 000 r/min

6 结论

通过对绕丝结构化砂轮的建模，结合磨粒运动轨迹方程，理论分析和软件仿真出微沟槽形貌创成机理和磨削参数对沟槽形貌的影响。根据磨削实验得出绕丝结构砂轮能够磨削沟槽结构。仿真和实验结果表明：绕丝结构化砂轮可以平面磨削出结构化沟槽表面，且改变磨削用量能磨出不同尺寸的参数与排布的沟槽结构。