基于数值模拟的2种条纹沟槽减阻特性对比分析

杜淑雅, 桑为民, 庞润

(1.西北工业大学 航空学院, 陕西 西安 710072; 2.航空工业西安飞行自动控制研究所, 陕西 西安 710076)

对于面向商业应用的民航飞机,经济性是其关键的性能指标之一。而表面摩擦阻力的减小即使只有几个百分点也可以带来较大的收益。目前,流体力学中减小摩擦阻力的方法可以分为主动减阻和被动减阻2个大类。被动减阻是通过在物体表面布置微结构,使边界层的流动状态发生改变,从而实现减阻。最初,人们发现动物的皮肤表面具有许多细小的微结构。鲨鱼的皮肤上有许多与流动方向平行的凹槽,可以减小游动过程中的摩擦阻力[1];许多鸟类的羽毛具有V型的棱纹结构,可以减小飞行过程中的空气摩擦阻力[2]。条纹沟槽作为表面微结构的一种,对于飞机减阻的研究具有重要的意义。

早在20世纪70年代,人们就开始了对条纹沟槽的实验研究。NASA兰利研究中心的Walsh[3-6]发现,V形沟槽具有最佳的减阻效果,在跨声速条件下可以得到约6%的减阻。在此之后,Bechert、Bacher、Choi等[7-9]也都进行了大量的实验工作,并对条纹沟槽的减阻机理提出了不同的解释,但还没有形成一个统一的认识。因此,许多研究人员试图采用数值模拟的方法探究沟槽的减阻机理及影响规律。在1993年,Chu等[10]就采用高精度的谱方法研究了层流、转捩和湍流状态下沟槽的减阻效果,结果表明沟槽只有在转捩和湍流条件下有较好的减阻效果。此后,Choi等[11]采用DNS方法模拟了三角形沟槽的减阻效果。Choi指出:减阻型沟槽通过限制流向涡的位置使得只有沟槽尖端部分暴露在高速流体下,因此只有沟槽尖端部分阻力较大,其余部分阻力较小。如果沟槽尺寸过大,就会导致流向涡进入沟槽内部,使沟槽内大部分区域暴露在高速流体下,使阻力增大。Martin等[12]采用LES方法研究了刀刃形肋条的表面流场。Martin指出:流向涡的尺寸是沟槽间隔的1.5倍时,减阻效果最好。当流向涡的尺寸小于沟槽间隔时,沟槽起增阻作用。这一结果支持了Choi对沟槽减阻机理的解释。由此可见,在数值模拟方面,目前已对条纹沟槽的减阻机理形成了一些初步的认识,即条纹沟槽主要通过影响流向涡的位置实现一定的减阻或增阻效果。目前主流的观点认为影响条纹沟槽减阻效果的主要因素是沟槽的几何形貌和无量纲尺寸。

本文基于前人的研究结果,首先通过计算标准的槽道湍流并与直接数值模拟的结果进行对比,分析了RANS、DES和LES方法模拟非定常湍流边界层流动的准确性,得出LES方法可以用于研究沟槽表面边界层流场流动细节的结论。然后针对低速条件下,模拟了三角形与梯形沟槽流场,将计算得到的沟槽减阻率与实验结果和直接数值模拟的结果进行对比,从而验证了计算结果的准确性。通过沟槽流场的积分统计量、一阶统计量、二阶统计量和瞬时流场特性,分析了2种沟槽对流场的影响规律与减阻机理。通过进一步对比三角形沟槽和梯形沟槽流场参数的差异,分析沟槽形貌对沟槽减阻效果的影响,并且得出结论:在相同无量纲条件下,梯形沟槽相较三角形沟槽减阻效果更好。

1 数值方法

1.1 控制方程

尽管湍流边界层呈现出复杂的流动特性,其基本的流动行为仍然满足流体力学的基本控制方程,即纳维-斯托克斯方程(Navier-Stokes equations,N-S),不可压缩N-S方程的具体形式为:

连续性方程

(1)

动量方程

(2)

式中:ui表示流体不同方向的速度分量;xi表示不同方向的空间坐标；t表示时间;ρ表示流体的密度;p表示流体的压力;ν表示流体的运动黏性系数;fi表示作用在流体微元不同方向上单位质量的体积力。

1.2 数值模拟方法

对于湍流问题的数值模拟,目前常用模拟方法有雷诺平均方法(Reynolds averaged Navier-Stokes,RANS)、大涡模拟方法(large eddy simulation,LES)、直接数值模拟方法(direct numerical simulation,DNS)等。RANS方法计算量小,可以较好地分析升阻力等宏观特性。但由于RANS方法只能给出湍流的时均运动和相应的时均物理量,不能给出相应的脉动量,并且目前还没有一个普适的湍流模型,因此RANS方法对于复杂的非定常湍流流动问题如湍流边界层流动还难以达到令人满意的效果。DNS方法直接求解N-S方程,在所有的时间尺度和空间尺度上对流动参量进行求解,是理论上最精确的方法。但由于湍流的多尺度特性,DNS方法需要巨大的网格量和很小的时间步长,因此目前只能对一些十分简单的外形和较小的雷诺数进行模拟。LES方法采用滤波方法,模拟大尺度漩涡,对小尺度脉动进行建模。LES方法的网格量介于RANS和DNS之间,是目前具有较好适用性的一种方法。

1.3 几何建模与网格生成

典型的三角形与梯形沟槽减阻特性曲线如图1所示[7]。图中纵坐标为不同沟槽的减阻率,横坐标s+为沟槽的无量纲尺寸,具体定义为

(3)

式中,Uτ定义为相同来流条件下,光滑平板的剪切速度[7]。当s+≤18时,沟槽的减阻效果随无量纲尺寸s+的增加而增加;当s+>18时,沟槽的减阻效果随无量纲尺寸s+的增加而减小。由此,选择2种具有典型流动特征的沟槽尺寸,s+=18和s+=36。其中s+=18的沟槽被称为“减阻型沟槽”,而s+=36的沟槽主要起增阻的效果,被称为“增阻型沟槽”。采用大涡模拟方法模拟这2种尺寸沟槽的流场特征,选取几何特征分别为α=60°的三角形沟槽和α=30°,h=0.5s的梯形沟槽。

图1 三角形与梯形沟槽减阻特性曲线对比[7]

在槽道Y方向的下表面分别布置2种条纹沟槽,计算基于δ(槽道半高度)和平均速度Um的雷诺数约为2 800。对于三角形沟槽,采用Y型网格拓扑,近壁面第一层网格y+<1。对于梯形沟槽,网格拓扑较为简单,近壁面第一层网格y+<1。沟槽内网格的划分情况如图2所示,近壁面网格正交性良好,网格尺寸过渡较为光滑,网格质量良好。经过换算,2种条纹沟槽的有量纲尺寸s为0.5和1.0 mm。

图2 三角形与梯形沟槽内网格拓扑示意图

2 算例验证

2.1 计算域的设置

参考前人数值模拟[9]和实验研究[7]的结果,将计算域设置为如图3所示的槽道流动,尺寸为Lx×Ly×Lz。采用商用软件Fluent求解槽道流动,X方向为来流方向,在X方向的ABCD面和EFGH面采用周期性边界条件。Z方向的ABFE面和DCGH面同样采用周期性边界条件,Y方向的ADHE面和BCGF面采用无滑移绝热壁面边界条件。在验证算例中,Y方向的ADHE面和BCGF面均设为光滑壁面。在模拟微结构表面边界层流动时,在BCGF面布置条纹沟槽,并通过比较ADHE面和BCGF面流场参数的差异获得沟槽表面的流动特性。

图3 计算域的设置

除了边界条件以外,计算域的大小和网格的设置对于数值模拟的准确性同样十分关键。计算域的大小合适与否前人已经发展出了不同的测试方法和经验理论,例如Kim等[13]指出对于周期性的流场可以采用检测两点相关性的方法来验证计算域的大小是否合适。张子良[14]在他的博士论文中指出选用X,Y,Z方向尺寸为2πδ×2δ×2δ的计算域可以满足计算要求。其中δ指槽道计算域Y方向(法向)有量纲长度的一半,即槽道的半高度。设置计算域X方向长度为50 mm,无量纲长度为1 800;Y方向和Z方向长度均为10 mm,无量纲长度为360,满足张子良提出的要求。

为了验证数值模拟方法的准确性,采用与文献[13]相同的雷诺数进行计算。以槽道Y方向的高度2δ为参考长度,以平均速度Um为参考速度,模拟的雷诺数Re为5 600。

在RANS方法中,较为常用的湍流模型有Spalart-Allmaras(S-A)单方程模型、k-ε两方程模型、k-ω两方程模型、雷诺应力(Reynolds stress)模型等,并与LES和DNS方法比较。在LES方法中,采用动态的Smagorinsky-Lilly模型,指定X方向出入口的压力梯度,数值格式采用SIMPLE算法,时间推进采用二阶隐式格式。无量纲时间步长取0.001,积分总时间取100。在DES方法中,在近壁面采用S-A湍流模型,在远离壁面处采用大涡模拟方法,时间推进格式和时间步长的选取与LES方法相同。各湍流模型使用相同的网格。

2.2 结果分析

2.2.1 积分统计量与一阶统计量的对比

表1给出了采用RANS方法、DES方法和LES方法得到的平板阻力系数与DNS结果[13]对比。DNS方法得到的光滑平板阻力系数为8.18×10-3。由表1可知,3种方法均可以较好地预测光滑平板的阻力。通过比较,可以发现在RANS方法中S-A模型对阻力模拟的效果更好。因此在接下来RANS结果的呈现中,湍流模型均为S-A模型。表2给出了其他时均流动参量与DNS结果的比较,可以看到,不同的模拟方法得到的边界层参数与DNS结果符合良好。图4给出了不同数值方法得到的平板表面速度型与DNS结果的对比,可以发现,RANS、DES和LES方法均可以较为准确地模拟时间平均速度在近壁面的分布。

图4 不同数值方法得到的槽道湍流近壁面时均速度分布

表1 不同数值方法得到的光滑平板阻力系数对比

表2 不同数值方法得到的槽道湍流时均流动参数

2.2.2 瞬时流场与二阶统计量的对比

DES方法最终未能得到任何的速度脉动,整个流场呈现一种定常状态,即使采用DES方法时选择的是非定常求解器。由此可见,在当前设置下,DES方法未能给出湍流边界层内的二阶统计量分布,而RANS方法对速度脉动进行了模化,因此同样无法给出速度脉动等二阶统计量的分布。因此接下来对于二阶统计量的分析，只给出LES的结果并和DNS结果进行对比。

图5a)给出了X,Y,Z方向上速度脉动均方根的分布,速度脉动均方根的定义为：

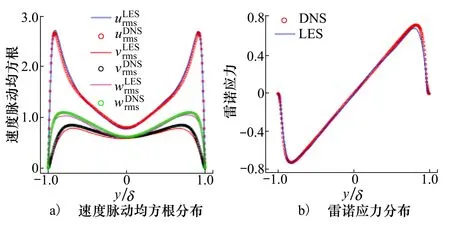
图5 槽道湍流近壁面二阶统计量分布情况

通过计算标准的槽道湍流并与直接数值模拟的结果进行对比,分析了RANS、DES和LES方法模拟非定常湍流边界层流动的准确性。LES方法相较RANS和DES方法对流动细节的刻画更为准确,LES方法除了可以较为准确地给出宏观升阻力和时均速度分布外,对二阶统计量的模拟如速度脉动均方根分布、雷诺应力分布均得到了与直接数值模拟相符合的结果。因此LES方法可以用于研究条纹沟槽表面边界层流场的流动细节,也是本文主要采用的数值方法。

3 三角形与梯形沟槽减阻特性对比

3.1 积分统计量与一阶统计量对比分析

3.1.1 宏观阻力与减阻率

表3～4分别给出了2种尺寸的三角形沟槽和梯形沟槽的宏观阻力系数与减阻率计算结果,并与实验值[7]进行了比较。其中，s+=36的梯形沟槽目前还没有完善的实验数据，因此表中未列出其减阻率的实验值。在减阻率一栏中,负值代表减阻,正值代表增阻。通过与相同无量纲尺寸的三角形沟槽进行对比可以发现,梯形沟槽的减阻率整体上优于三角形沟槽。

表3 三角形沟槽减阻率计算结果

表4 梯形沟槽减阻率计算结果

3.1.2 时均速度分布

本文中分别对2种沟槽选择具有代表性的观测点表征流场特征,观测物理量沿壁面法向的分布变化特性,图6分别给出了三角形和梯形沟槽内不同观测点的分布图。

图6 不同形状的条纹沟槽内观测点位置示意图

图7给出了具有相同无量纲尺寸的三角形沟槽和梯形沟槽的近壁面速度型分布对比。通过比较可以发现,梯形沟槽底部观测点处的速度型相较三角形沟槽底部处的速度型在黏性底层区域有明显上移,壁面处速度梯度相对较大。这表明梯形沟槽底部的减阻效果相较三角形沟槽底部较差。另外,梯形沟槽中部的速度型明显低于沟槽底部,表明梯形沟槽中部的减阻效果相较底部更好。梯形沟槽不同观测点处的速度型相较三角形沟槽重合地更快,梯形沟槽对流场的影响相对较小。此外,三角形沟槽的速度型在对数律区明显低于同尺寸的梯形沟槽,因此梯形沟槽相对于三角形沟槽具有更好的减阻效果。

图7 不同尺寸的2种沟槽近壁面速度分布对比

3.1.3 局部阻力特性

图8给出了三角形与梯形沟槽的沟槽顶部之间的局部减阻率分布,其中横坐标表示观测点距离沟槽顶部的展向距离,并采用沟槽宽度s进行无量纲化。局部减阻率RDR的定义为

(7)

式中:τriblets代表沟槽表面的局部剪应力;τsmooth代表光滑表面的局部剪应力。由图8可知,2种沟槽内大部分区域的阻力均小于上表面光滑平板的阻力。对于三角形沟槽,沟槽底部的减阻效果更好,而沟槽顶部处的阻力明显大于上平板阻力。在三角形沟槽底部,局部减阻率接近100%,这表明在沟槽底部存在安静的低速流体,低速流体与壁面的摩擦阻力很小。对于梯形沟槽,沟槽中部具有最佳的减阻效果,而沟槽底部的减阻效果有所下降。与三角形沟槽相比,尽管梯形沟槽底部的减阻效果有所下降,但梯形沟槽顶部附近增阻的负面效果明显有所改善,并且梯形沟槽减阻区域所占的比例相较三角形沟槽明显更大。在沟槽顶部附近,梯形沟槽的局部阻力特性变化相较三角形沟槽更加剧烈,局部阻力下降较快。因此,尽管三角形沟槽底部的减阻效果优于梯形沟槽,但梯形沟槽大部分区域内的减阻效果更好。

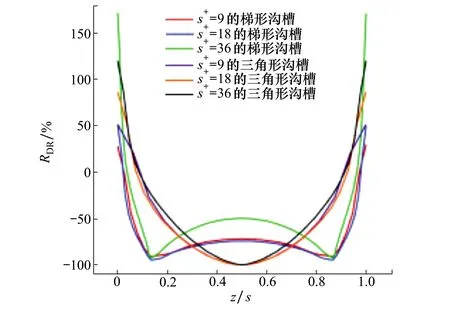
图8 不同尺寸的三角形与梯形沟槽局部减阻率分布

不同形状的沟槽在尺寸发生变化时局部阻力特性也会发生不同的变化。对于三角形沟槽,沟槽尺寸发生变化时主要是沟槽顶部附近的局部阻力特性发生了明显变化。随着无量纲尺寸增加,沟槽顶部附近的阻力明显增大,而底部附近的局部阻力变化较小。而对于梯形沟槽,随着沟槽尺寸发生变化,尽管沟槽顶部附近的局部阻力峰值明显上升,但由于局部阻力变化剧烈, 即使局部阻力的峰值增加也能很快地恢复到减阻状态。阻力发生明显上升的区域所占的面积较小，因此沟槽顶部附近总的阻力变化较小。而沟槽底部的阻力明显发生变化,随着沟槽尺寸的增加,沟槽底部的局部阻力先减小后增大。对于三角形沟槽,沟槽顶部附近的阻力特性决定了沟槽整体的减阻效果。对于梯形沟槽,主要是沟槽底部附近的阻力特性决定了整体的减阻效果。

3.1.4 时均流场特性

由图9～10给出的2种沟槽时均速度可知,梯形沟槽与三角形沟槽类似,内部存在低速流体,这些低速流体起到了缓冲的作用,避免条纹沟槽壁面与外层的高速流体直接接触。对于s+=36的2种沟槽,可以明显看到沟槽外的高速流体侵入了沟槽内部,并在沟槽中部和沟槽顶部附近形成了较大的速度梯度,由此引发剪应力急剧上升,减阻效果下降。与三角形沟槽相比,随着沟槽无量纲尺寸增加,梯形沟槽内高速流体侵入的范围明显更大。在三角形沟槽底部附近,速度梯度始终较小,高速流体对三角形沟槽底部的影响较小。而对于s+=36的梯形沟槽,可以明显看到高速流体十分接近沟槽底部,导致沟槽底部的阻力特性变化较大。因此在高速流体侵入程度相同的情况下,三角形沟槽底部受高速流体的影响较小。

图9 不同尺寸的三角形沟槽表面时均速度云图 图10 不同尺寸的梯形沟槽表面时均速度云图

图11～12给出了三角形与梯形沟槽横截面上Z方向的时均涡量云图。X方向的时均涡量幅值较小,对流场的影响较小,而在沟槽表面,Y和Z方向幅值相当,因此本文中仅给出Z方向的涡量。Z方向的涡量主要集中在沟槽顶部及附近区域。

图11 三角形沟槽近壁面Z方向时均涡量云图 图12 梯形沟槽近壁面Z方向时均涡量云图

通过相同无量纲尺寸的三角形与梯形沟槽对比发现,三角形沟槽底部始终保持较小的涡量分布,几乎没有涡量的作用,而在顶部附近Z方向涡量的作用面积明显大于梯形沟槽。这表明三角形沟槽底部流体的稳定性高于梯形沟槽底部,因而三角形沟槽底部的局部阻力特性更好;而三角形沟槽顶部由于Z方向涡量的作用,阻力明显大于梯形沟槽。随着沟槽无量纲尺寸的增加,梯形和三角形沟槽Z方向涡量在顶部附近都呈现出了下沉的趋势,但三角形沟槽下沉的范围明显更大。

3.2 二阶统计量对比分析

3.2.1 速度脉动均方根分布

图13给出了2种沟槽Z方向速度脉动均方根分布,X、Y方向变化趋势与Z方向类似,故本文不再赘述。采用槽道中心线的时均速度Uc进行无量纲化。由图可知,梯形与三角形沟槽类似,减阻型沟槽减小了Z方向速度脉动均方根的峰值,并且沟槽对速度脉动量的影响只局限在靠近壁面的范围,远离壁面后沟槽不同位置的速度脉动曲线发生重合。增阻型沟槽却增加了Z方向的脉动速度峰值。随着沟槽尺寸的增加,峰值所在的位置离壁面越远。梯形沟槽的脉动速度峰值均小于相同无量纲尺寸的三角形沟槽,并且三角形沟槽对流场的影响更大。三角形沟槽和梯形沟槽都将速度脉动的峰值向远离壁面处推迟,但三角形沟槽推迟的距离更远。

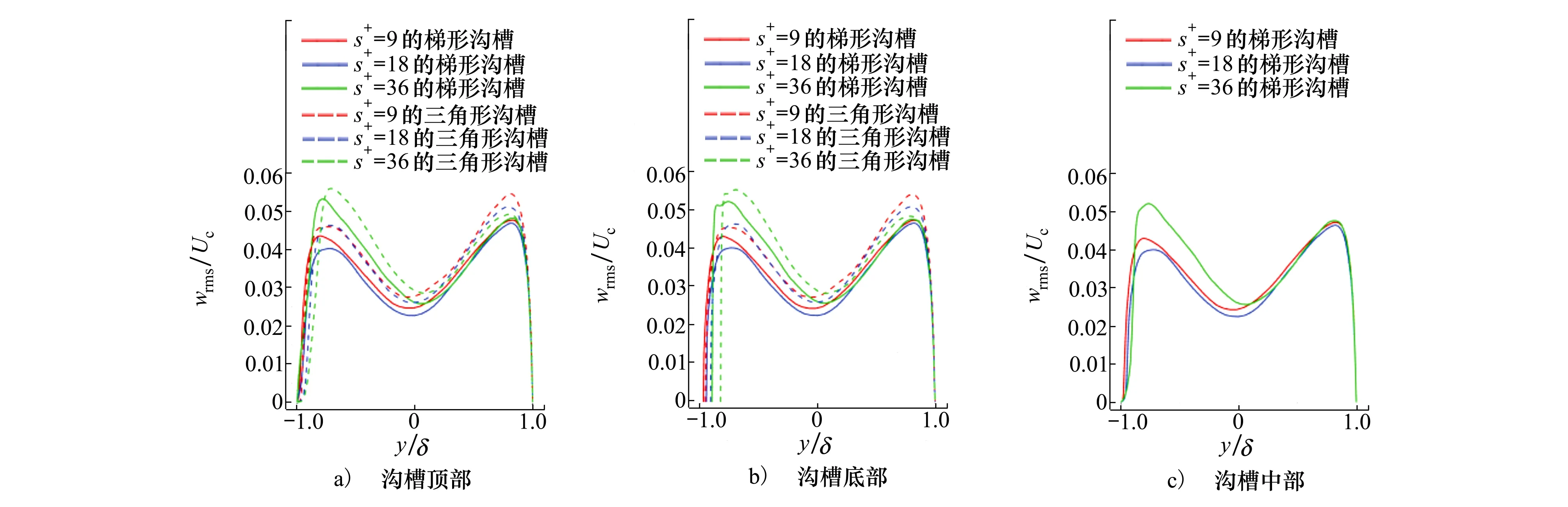
图13 2种沟槽Z方向速度脉动均方根分布

3.2.2 剪应力分布

图14给出了2种沟槽表面不同位置总剪应力分布，并且槽道中线的时均速度Uc进行无量纲化。由图可知,在梯形沟槽的底部和中部,随着沟槽无量纲尺寸的增加,沟槽近壁面处的总剪应力单调下降。但对于增阻型沟槽(s+=36),远离壁面后总剪应力明显大于减阻型沟槽(s+=9和s+=18)。在沟槽顶部,减阻型沟槽的总剪应力分布基本相同,而增阻型沟槽的总剪应力明显更大。与三角形沟槽相比,梯形沟槽顶部附近的总剪应力较小,而底部附近的总剪应力尽管在近壁面处大于三角形沟槽,但峰值却明显小于三角形沟槽。

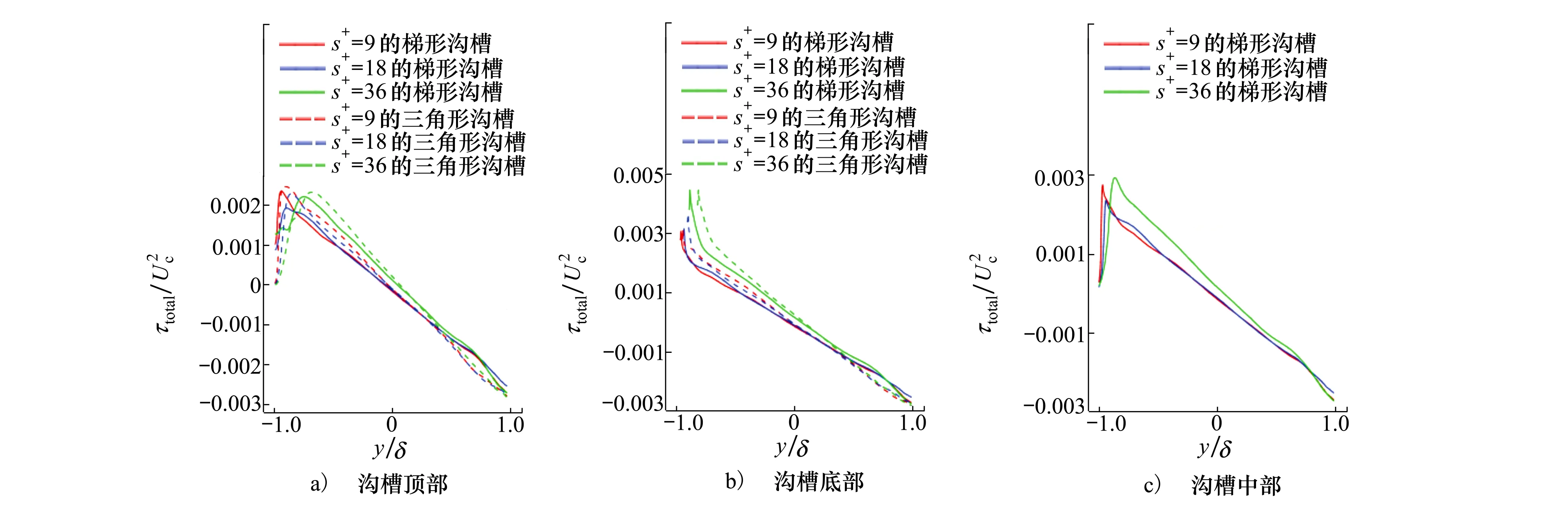
图14 2种沟槽表面不同位置总剪应力分布

3.2.3 湍动能的生成

图15和图16给出了三角形与梯形沟槽表面流场的湍动能生成项分布云图。2种沟槽类似,随着沟槽尺寸的增加,湍动能的生成项减小,并逐渐向壁面靠近,在尺寸为s+=36时进入沟槽内部。对于减阻型沟槽,湍动能的生成在壁面附近分布较为均匀;但对于增阻型沟槽,湍动能生成项的幅值在沟槽的不同位置呈现显著差异,沟槽顶部处的幅值最大。与相同无量纲尺寸的三角形沟槽相比,梯形沟槽表面湍动能生成项的幅值较小,因此减阻效果更好。

图15 不同尺寸三角形沟槽ZY截面湍动能生成项分布云图 图16 不同尺寸梯形沟槽ZY截面湍动能生成项分布云图

3.3 瞬时流场对比分析

图17和图18分别给出了不同尺寸的三角形与梯形沟槽顶部所在的XZ平面的展向脉动速度,法向脉动速度云图与展向变化规律类似,故本文不再赘述。与相同无量纲尺寸的三角形沟槽相比,梯形沟槽顶部的展向脉动速度明显更小,这表明梯形沟槽内的低速流体相较三角形沟槽更加稳定,因此减阻效果更加显著。

图17 三角形沟槽顶部所在的XZ平面展向脉动速度云图 图18 梯形沟槽顶部所在的XZ平面展向脉动速度云图

图19和20分别给出了三角形与梯形沟槽在XZ截面以Q准则[15]为标度的涡结构分布。可以发现,减阻型梯形沟槽较好地抑制了近壁面涡结构的产生,而增阻型沟槽则起到了相反的效果。与具有相同无量纲尺寸的三角形沟槽相比,梯形沟槽近壁面的涡结构数量明显少于三角形沟槽,因此梯形沟槽对涡结构的限制效果更好,减阻效果更加显著。

图19 s+=18的不同沟槽XZ截面涡结构分布示意图 图20 s+=36的不同沟槽XZ截面涡结构分布示意图

4 结 论

本文采用大涡模拟方法模拟了三角形与梯形沟槽流场,通过与Bechert[7]的实验结果进行对比,验证了计算结果的准确性。通过比较三角形沟槽和梯形沟槽流场参数的差异,分析沟槽形貌对沟槽减阻效果的影响,基本结论如下:

1) 梯形沟槽对流场的影响与三角形沟槽基本相同,但梯形沟槽的减阻效果更好。

2) 对于梯形沟槽,沟槽中部具有最佳的减阻效果,而沟槽底部的减阻效果有所下降。与三角形沟槽相比,梯形沟槽顶部附近增阻的负面效果明显有所改善,并且梯形沟槽减阻区域所占的比例相较三角形沟槽明显更大。

3) 梯形沟槽的沟槽底部存在Z方向涡量的作用,由此导致梯形沟槽底部附近的减阻效果不如三角形沟槽。

4) 与相同无量纲尺寸的三角形沟槽相比,梯形沟槽表面湍动能生成项的幅值和涡结构的数量较小,因此减阻效果更好。