基于表面V形沟槽的圆柱减阻性能研究
江兴隆,欧阳凌浩,李 超
(中国船舶集团有限公司第七一〇研究所,湖北 宜昌 443003)
0 引言
水下拖曳系统是进行海洋探测的重要手段,广泛应用于海洋环境监测、资源勘探、军事等众多领域。进行大深度拖曳时,水下拖曳系统的阻力主要由拖缆产生[1]。拖缆的阻力过大,导致定深变差,影响拖曳系统的工作性能。拖缆在水中的运动,可看为多段不同迎流角圆柱的运动,所以拖缆的减阻可看作多段圆柱的减阻,本文采用表面沟槽的减阻方式来减小圆柱阻力。
Walsh等人[2]最先开展沟槽减阻性能的研究,并发现对称的 V型条纹沟槽表面在湍流条件下可减阻8%。Bechert和Brused[3]测试了多种形状的沟槽条纹,V型沟槽减阻效果可达10%。Lim[4]通过在圆柱体上横向布置O形圈,对圆柱绕流进行控制,最大有9%的减阻效果。Quintavalla S J[5]发现低深径比沟槽可以显著降低绕流阻力,且所有沟槽占总圆柱截面积比值会影响临界雷诺数。Huang S[6]在拖曳水池测量了矩形沟槽圆柱的绕流升阻力。王沣浩[7]设计了一种波状圆柱,其脉动升阻力系数减小,并通过实验得到最大减阻效果为20%。廖崇吉[8]进行了沟槽圆柱体的数值仿真计算,在雷诺数Re=40 000时,最大减阻率为16.3%。钱权[9]开展了V型沟槽圆柱绕流数值模拟研究,最大减阻率可达28.4%。齐野含[10]发现沟槽圆柱能够抑制表面旋涡的影响区域范围,提高旋涡的流向尺度,并通过水槽试验验证了仿真结果。
目前,国内外关于沟槽减阻研究已经有很多,但很少对有一定倾斜角的沟槽圆柱进行研究,表面沟槽对拖缆的减阻也还未形成系统的研究。本文对V形沟槽圆柱的减阻研究,讨论了沟槽参数、雷诺数及迎流角对减阻性能的影响,对今后沟槽缆的实际设计使用具有一定的参考价值。
1 V形沟槽圆柱模型
1.1 几何模型
圆柱直径D=20 mm,V形沟槽沿圆柱的周向均匀分布。沟槽的尺寸主要由3个参数确定,分别为沟槽深度h、沟槽宽度s、沟槽数量n,得到如图1所示的模型示意图。

图1 沟槽圆柱模型图Fig.1 Model diagram of groove cylinder
1.2 沟槽深度尺寸确定
Walsh等人[1]对沟槽平板的减阻性能研究可知:无量纲沟槽深度h+≤25时,沟槽具有很好的减阻效果,本文借鉴该研究成果进行沟槽圆柱的参数设计。
无量纲沟槽深度:

壁面剪切速度:

壁面剪切应力:

边界层厚度:
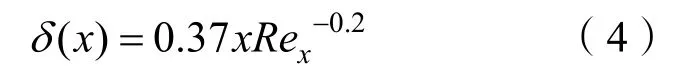
由式(3)和(4)代入式(2),得:

从而得到无量纲沟槽深度为

式中:h为沟槽深度;U∝为来流速度;υ为运动粘性系数。
来流速度为2 m/s、h+取为25时,通过式(6)计算得到沟槽深度h=0.21 mm,即h≈0.01D,后续进行数值模拟时,沟槽深度在0.01D附近选取。
2 网格无关性分析
获得适合沟槽圆柱的仿真模型,确定影响仿真模拟的重要参数,使计算结果准确。在雷诺数Re=40 000、圆柱直径D=20 mm时,采用光滑圆柱进行仿真计算。
在保证流场不受边界尺寸影响的前提下,选择计算域20D×10D,前后边界面距离圆心5D,上游边界面距离圆心 5D,下游边界面距离圆心 15D,如图2所示。
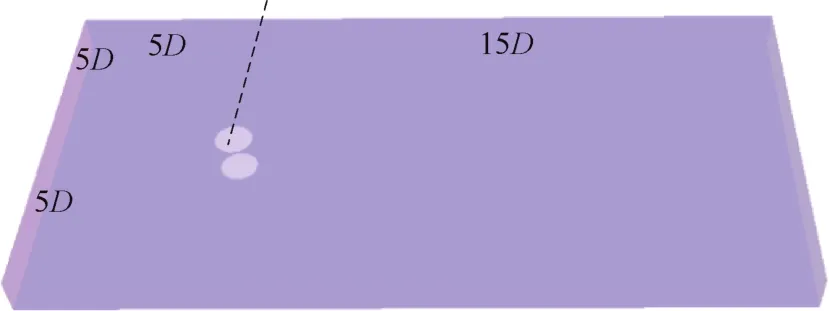
图2 计算域Fig.2 Computing domain
采用多面体网格进行全局的网格划分,该网格可很好地在小尺寸沟槽圆柱表面划分规则网格。在仿真计算中,采用SSTk-ω湍流模型,该模型算法稳定性好,可很好地模拟精细化局部流场,对物体近壁区的流场有很好的计算精度。该模型要求圆柱壁面到最近的网格节点高度的无量纲数y+≈1,当来流速度为2 m/s时,计算得出第1层边界层的高度为0.008 5 mm。

图3 计算域局部网格划分Fig.3 Computing domain local meshing
分别选取3种网格基准值0.018 m、0.015 m、0.012 m,测得平均阻力值如表1所示。

表1 不同网格尺寸比较表Table 1 Comparison table under different mesh sizes
从表中可看出,网格基准值为0.015 m、网格数目为147万时,阻力系数为1.19,与Norberg C的试验结果误差最小,网格基准值选为0.015 m。
3 数值模拟结果分析
第2章节得到了仿真模型的重要参数,即圆柱展长为D,网格基准值为0.015 m,用于V形沟槽圆柱的数值模拟。
3.1 雷诺数Re
迎流角θ=90°,雷诺数Re分别为 20 000、30 000、40 000、50 000时,模拟光滑圆柱和V型沟槽圆柱的平均阻力系数,得到如图4所示的变化曲线。

图4 不同雷诺数下升阻力系数的变化曲线Fig.4 Variation curves of drag coefficient under different Reynolds numbers
图4中,随雷诺数的增加,光滑圆柱的阻力系数变化不明显,阻力系数约为1.2。V型沟槽圆柱的升阻力系数随雷诺数的增加而呈现减小趋势,当雷诺数Re>40 000后,升阻力系数的变化较缓,具有很好的减阻效果。
3.2 沟槽参数
在雷诺数Re=40 000、迎流角θ=90°时,分别研究沟槽深度h、沟槽宽度s、和沟槽数量n对减阻效果的影响。
3.2.1 沟槽深度
分别仿真计算沟槽深度h为0.005D、0.007 5D、0.01D、0.012 5D、0.015D时,稳定时间段内V型沟槽圆柱的平均阻力系数,如图5所示。

图5 不同沟槽深度下阻力系数变化曲线Fig.5 Variation curves of drag coefficient under different groove depths
由图5看出,5种沟槽深度下的阻力系数均小于光滑圆柱,说明选取的沟槽深度都具有一定的减阻效果。当沟槽深度大于0.007 5D时,随h的增加,阻力系数变大;当沟槽深度小于0.007 5D时,随h的增加,阻力系数变小。可知,当h=0.007 5D时,沟槽圆柱具有最佳的减阻效果。
3.2.2 沟槽宽度
沟槽宽度s分别为0.055D、0.06D、0.065D、0.07D、0.075D时,计算稳定时间段内V型沟槽圆柱的平均阻力系数,如图6所示。

图6 不同沟槽宽度下阻力系数变化曲线Fig.6 Variation curves of drag coefficient under different groove widths
如图6所示,5种沟槽宽度的阻力系数均小于1.19,具有一定的减阻效果。当沟槽宽度s大于0.065D时,随s的增大,阻力系数变大,从图中趋势可判断,s增大到一定值后,可能会起到增阻效果;沟槽宽度s小于0.065D时,随s的减小,阻力系数变大,光滑圆柱即s=0,不再具有减阻效果。当s=0.065D时,阻力系数最小,减阻效果最佳。
3.2.3 沟槽数量
沟槽数量n分别为24、30、36、40时,计算稳定时间段内 V型沟槽圆柱的平均阻力系数,如图7所示。

图7 不同沟槽数量下阻力系数变化曲线Fig.7 Variation curves of drag coefficient under different groove numbers
图7中,沟槽数量n小于36时,随着数量n的减小,阻力系数变大;沟槽数量n大于36时,阻力系数略微增加。当n=36时,阻力系数最小,减阻效果最佳。
3.3 迎流角
在迎流角θ分别为 90°、75°、60°、45°和 30°条件下,数值模拟计算光滑圆柱和 V型沟槽圆柱的时均阻力系数,得到5种迎流角下的阻力系数Cd和减阻率η的变化曲线,如图8所示。

图8 不同迎流角下减阻性能变化曲线Fig.8 Variation curves of drag reduction performance at different attack angles
图8中,2种圆柱的阻力系数Cd随迎流角θ的增加而增大。迎流角θ大于 45°时,光滑圆柱的阻力系数大于沟槽圆柱,沟槽结果产生减阻效果;迎流角θ小于 45°时,光滑圆柱的阻力系数小于沟槽圆柱,沟槽结构增阻,随θ的减小,增阻效果越明显。θ=90°时,减阻效果最好,减阻率达24%。
4 水槽试验结果分析
4.1 试验件
本次试验在哈尔滨工程大学的水槽实验室进行。由于试验的测力天平的测量量程影响,为尽量减小测量误差,试验件的长度取为200 mm。如图9所示,沟槽数量分别为36个、30个、24个的V形沟槽圆柱,长度为100 mm、200 mm的光滑圆柱,圆柱前端为M8的螺纹,后端为M8的螺纹孔。长度100 mm的光滑圆柱,与试验件的后端部相连,用于减弱圆柱端部绕流阻力的干扰。

图9 加工零件示意图Fig.9 Schematic diagram of machined parts
4.2 试验方案设计
首先,为消除水下圆柱底端绕流影响,测出1.0 m/s、1.5 m/s、2.0 m/s流速下100 mm圆柱在水下的受力情况。其次,在200 mm光滑圆柱和3种不同沟槽圆柱下端连接 100 mm圆柱,测量1.0 m/s、1.5 m/s、2.0 m/s流速下的阻力值。最后,第2次测得的阻力值减去第1次的阻力值,得到光滑圆柱和沟槽圆柱的真实阻力值。图10为安装示意图。

图10 试验装置的安装图Fig.10 Installation diagram of test equipment
4.3 试验数据分析
试验得到了光滑圆柱和3种沟槽数量圆柱的真实阻力,计算得到 V形沟槽圆柱的平均阻力系数Cd和减阻率η,如图11所示。

图11 不同雷诺数下各试验件的减阻性能变化曲线Fig.11 Variation curves of drag reduction performance of each test article under different Reynolds numbers
由图 11可知:随着雷诺数的增加,4种圆柱的平均阻力系数减小,且在雷诺数为40 000时,阻力系数最小。沟槽数量为36时,平均阻力系数最小,即减阻效果最好,减阻率可达25%;沟槽数量为24时,平均阻力系数与光滑圆柱相差不大,且雷诺数为30 000时,出现了增阻现象。
在雷诺数Re=40 000时,比较4种不同沟槽数量圆柱的仿真结果与试验结果,如图12所示。

图12 仿真结果和试验结果比较图Fig.12 Comparison between simulation results and test results
从图12可知,在雷诺数Re=40 000时,除沟槽数量为24个之外,仿真结果与试验结果非常贴近,证明该数值模拟方法是正确的,具有很高的可信度。
5 结束语
本文研究了不同仿真模型参数对计算精度的影响,以及不同沟槽参数、雷诺数和迎流角下,V形沟槽圆柱的减阻效果,并通过试验验证了仿真结果。具体结论如下:
1)采用数值仿真计算的方法,对比分析升阻力系数,确定网格基准值为0.015 m。
2)对比分析了不同沟槽参数的减阻性能,得到沟槽深度h=0.007 5D、沟槽宽度s=0.065D、沟槽数量n=36时,V形沟槽圆柱具有最好的减阻效果。
3)不同雷诺数下,光滑圆柱的阻力系数在1.2附近浮动,V形沟槽圆柱的阻力系数随雷诺数的增加而逐渐减小,最大减阻率为24%。
4)迎流角为90°时,V形沟槽圆柱的减阻效果最好,随迎流角的减小,减阻效果变差,迎流角45°不再具有减阻效果。在沟槽缆的设计使用时,V形沟槽应布置在水下迎流角为60°~90°的位置。
5)通过比较试验与仿真结果,发现两者结果基本吻合,说明模拟方法正确,仿真结果具有很高的可信度。

