沟槽表面对翼型绕流流场的气动作用研究

陈子龙，杨爱玲，陈二云，焦 跃

（上海理工大学 能源与动力工程学院/上海市动力工程多相流动与传热重点实验室，上海 200093）

叶片表面流动状态是决定旋转叶轮机械气动性能与噪声特性的关键因素。由于气体的黏性，气体流经叶片表面时会形成紧贴壁面的流体薄层。该薄层厚度小、黏性影响大，即所谓的流动边界层。流动边界层内速度梯度大，壁面黏性切应力大，而且边界层内涡流在叶片尾缘周期性地脱落，在某些条件下边界层还可能发生流动分离。这些正是叶片表面流动阻力增加、流动噪声源增强的根本原因。

为了提高叶片的气动特性及降噪性能，国内外学者从叶片结构优化、表面设计等方面做了大量的研究工作，试图从设计源头改善叶片的气动降噪性能。非光滑表面技术作为一门新兴的边缘学科，涉及仿生学、流体力学、声学等众多学科。目前，较为成熟的研究方法有涡流发生器［1-2］、疏水表面［3］、锯齿尾缘［4］、仿生非光滑表面［5-6］等。

流动边界层控制技术被美国NASA 研究中心列为21 世纪航空关键技术之一［7］。沟槽非光滑表面技术是流动边界层控制技术的重要分支。该方法通过改变物体表面形状，控制壁面湍流附面层的应力分布与涡流结构，达到流动控制的目的。NACA Langley 研究中心Walsh［8］最先开展了将微沟槽非光滑表面应用于平板减阻的研究，突破了表面越光滑阻力越小的传统思维方式，从而引起了各国研究者对非光滑表面减阻研究的兴趣。Sundaram 等［9］对来流攻角为0°～6°的NACA012翼型的沟槽减阻研究结果表明，减阻效果随来流攻角的增加而增加，最大减阻效果达13%。空中客车公司在A320 试验机机翼的70%表面贴上沟槽面薄膜，获得了1%～2%的节油效果［10］。杨林等［11］基于“凹槽”和“陷窝”技术对低雷诺数下涡轮流动损失控制进行了实验研究与数值分析，研究表明：凹槽结构的存在能加强流动掺混，促进分离泡转捩，有效降低叶栅总压损失系数。

目前相关学者们对沟槽非光滑表面技术的研究更多关注其减阻效果与工程应用，并取得了大量研究成果［12-14］。而关于沟槽内涡流结构及与下游湍流流动相互影响的研究相对较少。因此，对沟槽非光滑表面技术的湍流特性进行研究非常有必要。

本文基于NACA6510 翼型表面的二维圆弧型沟槽为研究对象，通过数值方法研究沟槽相对位置及相对深度的变化对翼型表面湍流流动的影响，为沟槽非光滑表面技术在流动噪声控制应用提供理论基础。

1 计算模型和数值计算方法

1.1 几何模型和网格划分

图1 为NACA6510 翼型表面二维圆弧型沟槽几何示意图，其中：翼型弦长c=100 mm，沟槽位于翼型吸力面；x表示弦向坐标；λ、h分别表示沟槽的流向长度和深度。本文改变沟槽相对深度h/λ及沟槽在弦长方向的相对位置x/c获得15 组不同的翼型模型，沟槽几何参数如表1 所示。通过二维非定常湍流流场模拟分析上述参数对沟槽内外流动、翼型表面湍流的影响规律。

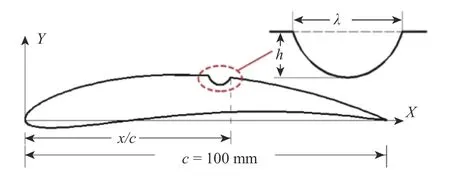
图1 NACA6510 翼型圆弧型沟槽几何示意图Fig.1 Sketch of the arc-shaped groove on NACA6510 airfoil

表1 沟槽几何参数Tab.1 Geometric parameters of the groove

计算时采用二维结构网格。为节省计算资源，将计算域划分为A、B 两个子域，数值计算域示意图如图2 所示。子域A 为外流场，长20c、宽16c，保证远场边界条件。内部子域B 长3.5c、宽2c、尾迹2c。子域B 采用O 型拓扑结构进行网格离散，两个子域交接面的网格一一对应。沟槽翼型网格数为140 万～160 万，其中子域B 网格数为110 万～125 万。

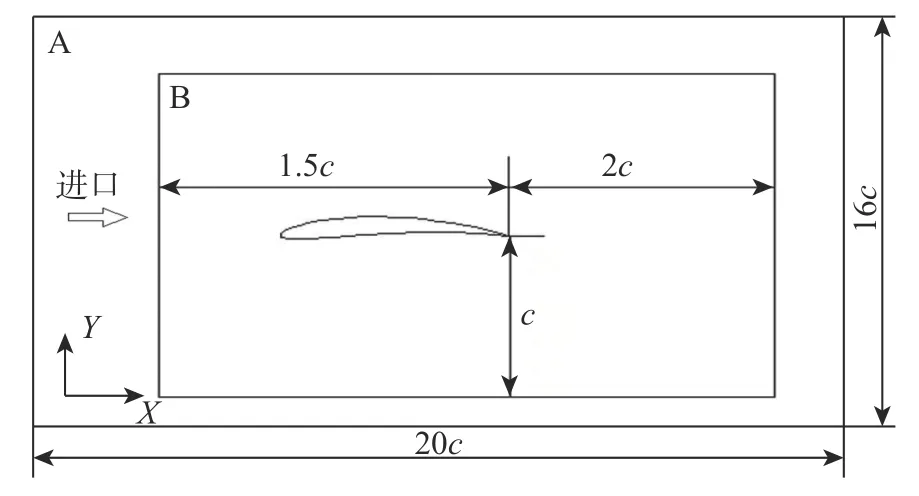
图2 数值计算域示意图Fig.2 Schematic diagram of the computation field

沟槽几何尺寸较小，为提高网格精度，对翼型近壁区、沟槽附近进行局部加密，近壁第一层网格高度为0.01 mm，确保Y+≤1，沟槽内部采用C 型拓扑。沟槽表面翼型网格示意图如图3 所示。

图3 沟槽表面翼型网格示意图Fig.3 Mesh of the airfoil with groove

1.2 控制方程及边界条件

运动马赫数Ma＜0.3的空气绕翼型流动，形成绕翼型的不可压湍流流场。本文采用二维不可压缩大涡模拟方法(large eddy simulation，LED)求解该翼型外部湍流场。大涡模拟方法求解瞬时N−S 方程获得大于计算网格尺度的湍流运动，而小尺度涡对大尺度涡的影响则通过亚格子应力模型体现。对于变量 φ，空间滤波后变为

式中：D为流动区域；G(x,x′)为滤波函数。

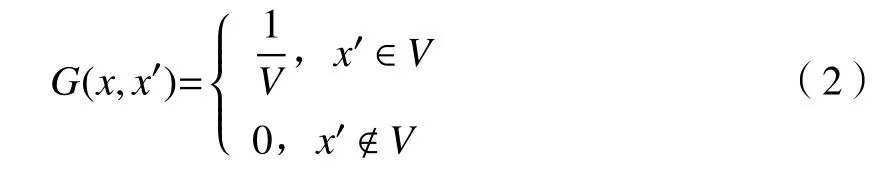
式中，V为控制体体积。

将式(2)代入式(1)可得

利用式(3)处理连续性方程及瞬时N−S 方程，可得二维不可压缩大涡模拟运动方程［15］，即

式中：ρ、µ 分别为空气密度、分子黏度；u为速度分量；p为修正压力；τij表 示亚格子应力，τij=，通过它可以体现小尺度涡对大涡运动方程的影响；带有上划线的为滤波后的变量；t为时间。

为使运动方程封闭，采用Smagorinsky−Lilly亚格子模型，即

式中：µt为亚格子湍流黏性系数；Δ 为网格尺度；Cs为 亚格子常数；Sij为网格平均应变率。

流动方程采用二阶迎风格式离散，基于SIMPLEC 算法实现速度场和压力场分离迭代求解。计算域进口给定速度边界条件，来流速度V=30m·s−1，基于翼型来流速度与弦长雷诺数Re=2×105。计算域出口位于翼型下游11倍弦长处，采用自由出流条件，翼型物面及沟槽采用无滑移绝热条件。时间步长 Δt=1×10−5s，监测翼型升力系数呈明显周期性变化后，推进10 000步作为非定常流场信息。大涡模拟计算时，采用SSTk−ω湍流模型求解RANS 方程，将时均收敛解作为非定常流场计算的初场。

2 计算结果与分析

2.1 计算方法验证

为验证数值计算结果的准确性，计算验证时采用Selig等［16］的经典实验，实验模型为E387翼型，弦长为0.304 8 m，基于弦长的雷诺数Re=2×105。验证时采用与本文相同的网格拓扑结构及计算方法。图4 为E387 翼型极曲线试验数据与本文模拟值的对比，图中横坐标Cd为阻力系数，纵坐标Cl为升力系数。可见，数值计算结果与实验结果保持一致，表明本文数值计算方法可行。

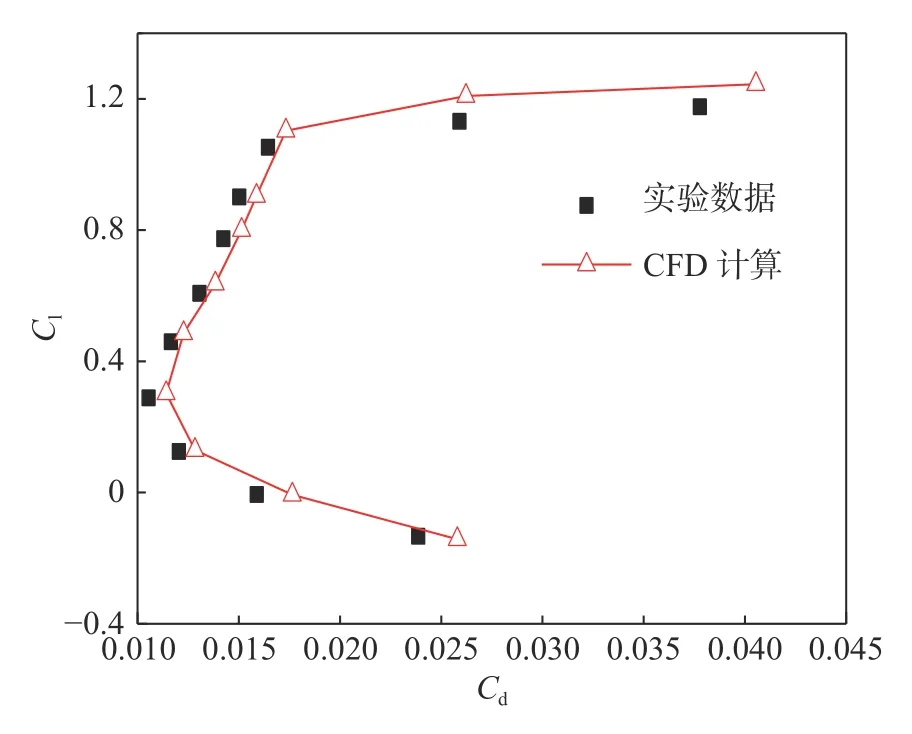
图4 E387 翼型极曲线Fig.4 Polar curve of E387 airfoil

2.2 翼型气动性能及绕流流场特征

极曲线反映了翼型的升、阻力特性，是翼型重要的气动数据之一［16］。图5为雷诺数Re=2×105，来流攻角α分别为0°、3°、6°、···、18°时NACA6510 翼型极曲线，其中：图5(a)给出了相对深度h/λ=0.35 时翼型极曲线随沟槽相对位置x/c的变化；图5(b)则为x/c=0.65 时沟槽深度对翼型极曲线的影响。由图5(a)可知：小攻角下沟槽相对位置对翼型升、阻力几乎没有影响；随来流攻角增加，影响逐渐明显，在α=18°时，沟槽使翼型阻力系数和升力系数减小，相对位置x/c=0.65 时，阻力系数从光滑翼型的0.226 5 减小为0.162 5，下降了28.26%。图5(b)表明，大来流攻角下沟槽深度对翼型升、阻力有较明显的影响。当相对深度h/λ=0.35 时，阻力系数从光滑翼型的0.226 5 减小为0.169 1，减少了25.34%；升力系数从光滑翼型的1.743 9 减小为1.437 5，下降了17.57%，阻力系数的减少量大于升力系数的减少量。

图5 NACA6510 翼型极曲线Fig.5 Polar curves of NACA6510 airfoil

图6 给出了来流攻角α=6°、t=0.135～0.140 s、沟槽相对位置x/c=0.65 时NACA6510 翼型升力系数时域曲线随相对深度h/λ的变化。可见，升力系数随时间呈明显的周期性波动。根据流体力学理论可知，这正是翼型尾缘周期性涡流脱落引起的升力脉动。表2 为α=6°、x/c=0.65 时经快速傅里叶变换（FFT）后获得的翼型升力系数脉动主频及对应的幅值，在沟槽相对深度小于0.35时，脉动频率几乎不变，但对应的峰值有变化。随相对深度进一步增加，当h/λ=0.50 时，升力系数脉动频率出现突变，频率明显减小。

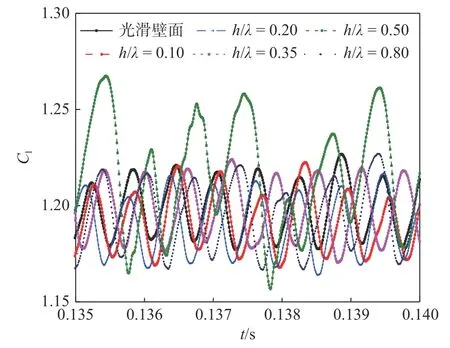
图6 升力系数时间历程Fig.6 Time history of lift coefficient

表2 不同相对深度沟槽升力系数脉动主频及对应的幅值Tab.2 Main fluctuation frequency and the corresponding amplitude of lift coefficient for the groove with various relative depth

为观测翼型近壁区流场压强脉动，在翼型吸力面侧设置g、p、f三个监测点，如图7 所示。监测点g位于0.3 倍弦长位置，离吸力壁面2 mm处；监测点p在凹坑内部监测点f则位于0.8 倍弦长位置，离吸力壁面2 mm 处。

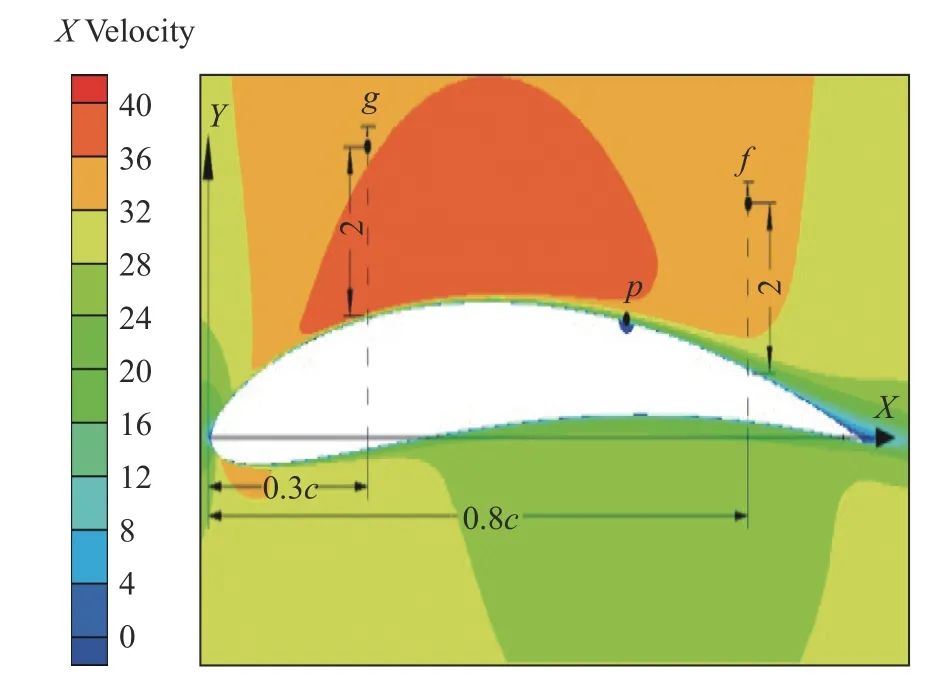
图7 监测点示意图Fig.7 Distribution of monitor points

图8 为沟槽相对深度h/λ=0.35 时监测点f的压强脉动在频域的分布，表3 为α=6°、h/λ=0.35 时的主频及对应幅值。可见，该监测点压强脉动在频域的分布呈明显的离散特性，具有沟槽的翼型压强脉动峰值均小于光滑翼型，且主脉动峰值随沟槽相对位置增加而减小，当x/c=0.75时，峰值由光滑翼型的225.11 Pa 减小为110.43 Pa，降幅为50.9%。从表3 还可知，相对位置x/c=0.55、0.75 时，压强脉动频率均有所降低。

表3 不同相对位置沟槽监测点f 压强脉动主频及对应幅值Tab.3 Main frequency and the corresponding amplitude of pressure fluctuation at point f for the groove at different relative positions

图8 不同相对位置沟槽监测点f 压强脉动频谱Fig.8 Pressure fluctuation spectrum of point f for the groove at different relative positions

表4 为来流攻角α=6°、相对位置x/c=0.65时不同相对深度沟槽表面翼型及光滑翼型监测点f的压强脉动主频及对应幅值。由表4 可知，同一相对位置下，随着沟槽深度的增加，监测点f脉动幅值呈先降后升的分布趋势，h/λ=0.35 时脉动幅值达到最小。表4 同时表明，沟槽较浅(h/λ=0.10、h/λ=0.20、h/λ=0.35)时，沟槽的存在对频率的影响较小；沟槽达到一定深度(h/λ=0.50、h/λ=0.80)后，压强脉动频率发生突变，脉动频率减小了110 Hz。监测点f压强脉动的频谱特性与翼型升力系数（参见表2）的变化吻合。通过上文分析说明，翼型吸力面的沟槽结构会改变下游涡流脱落频率和幅值。

表4 不同相对深度沟槽监测点f 压强脉动主频及对应幅值Tab.4 Main frequency and the corresponding amplitude of pressure fluctuation at point f for the groove at different relative depth

2.3 沟槽内流动特征分析

气体流经翼型表面，部分流体进入沟槽，在沟槽内部形成复杂的流动状态。图9 为来流攻角α=6°、相对位置x/c=0.65 时沟槽内部时均速度及流线随相对深度h/λ的变化。当h/λ较小时，流体流过沟槽结构区域，在内部产生了一个反向、稳定的扁平状二次涡，流动速度较小。当h/λ=0.35 时，有更多较高能量流体流入沟槽内部，形成了一大一小两个反向涡对。反向涡对的大小随沟槽相对增加呈先增大后减小的趋势。当沟槽深度进一步增加到h/λ=0.8 时，高能量的大涡挤压沟槽内较小的涡，使之变小。

图9 沟槽结构内部时均速度及流线分布Fig.9 Distribution of mean velocity and streamline in the groove

图10(a)为来流攻角 α=6、x/c=0.65 时沿沟槽中心线l的时均速度分布，纵坐标ΔY指中心线上的观测点到光滑翼型表面的长度。相关定义如图10(b)所示，l为过凹坑圆心的直线，ΔY＜0表示监测点位于沟槽内部。由图10 可知，随壁面相对距离的增加，速度明显呈先增大后减少再增大的趋势，说明流体流经沟槽结构时在沟槽内部形成了漩涡。深径比对 ΔY＞0区域的速度分布剖面影响较小，但沟槽内部的速度分布发生明显变化。相对于光滑壁面，沟槽相对深度增加，沟槽内部速度增量越大，这与上文对沟槽内部速度流线图的分析相对应。

图10 沟槽中心线时均速度分布Fig.10 Distribution of mean velocity along the center of the groove

图11 为α=6°、x/c=0.65、h/λ=0.35 时沟槽内部瞬时流线在一个主脉动周期ΔT（ΔT为监测点p压强脉动主频对应的周期）内分布。可以看出，在6°来流攻角下，附面层在沟槽上游已形成小分离涡，沟槽内部的二次涡由于该上游分离涡的挤压、附面层流体的裹挟共同作用经历了产生、发展、脱落过程，无法稳定滞留在沟槽内部。

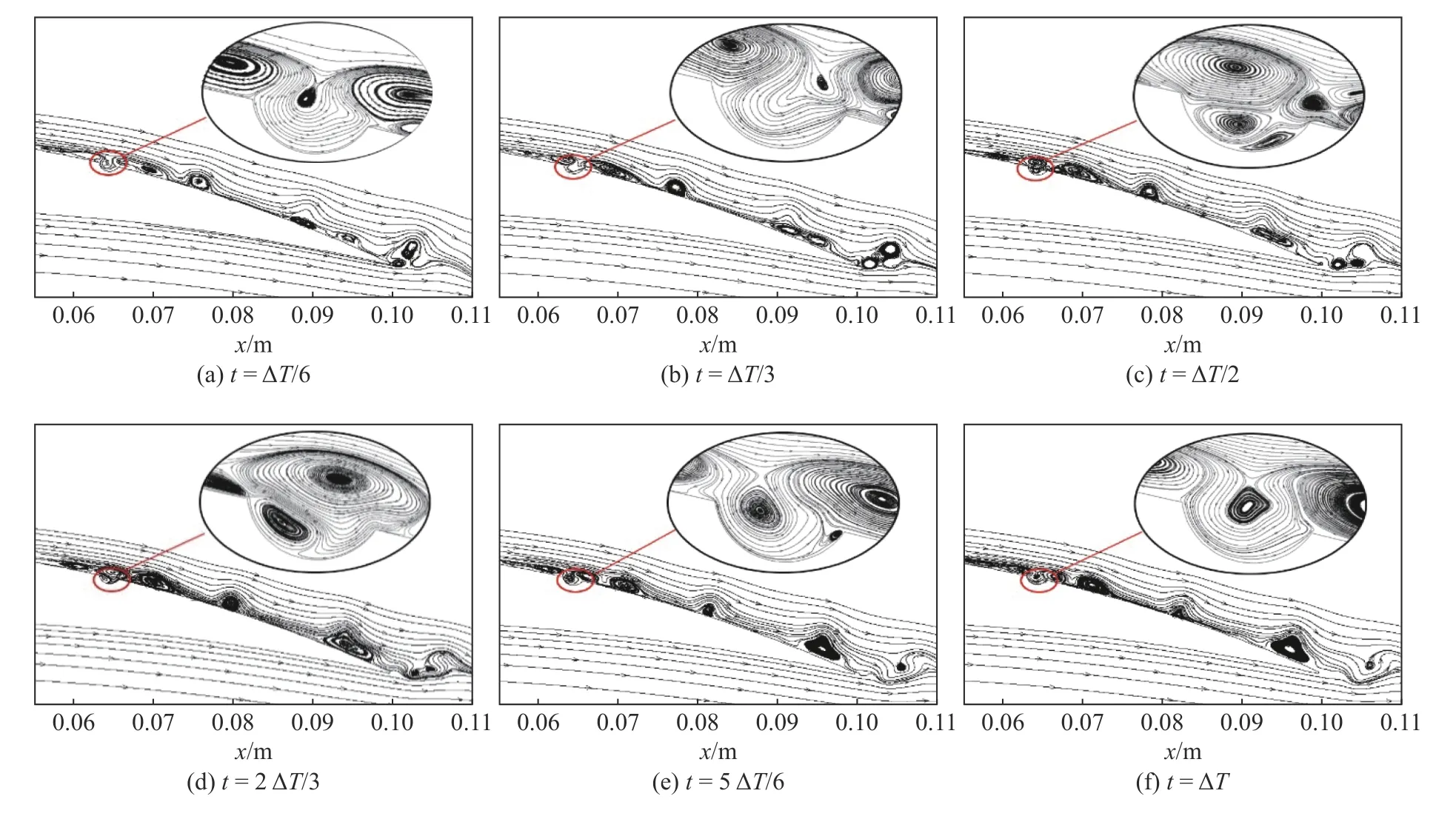
图11 1 个周期内各相位瞬时流线分布Fig.11 Distribution of instantaneous streamline during each phase of a period

图12 为α=6°、x/c=0.65、h/λ=0.35 时监测点g、p、f的压强脉动频谱分布（监测点位置如图7 所示）。可见，在沟槽上游的监测点g，压强脉动只在1 600 Hz 附近有较小的峰值，监测点的压强脉动在3 200 Hz 处出现了大小约35 Pa的峰值。该频率应为沟槽内部二次涡周期性产生、发展和脱落的频率，而在沟槽下游监测点f处，压强脉动在1 600、3 200 Hz 处均有明显的脉动峰，相较于g、p两点，监测点f的脉动幅值大幅增长。气体流经沟槽结构，翼型尾缘保持了上游及沟槽内部压强脉动的频率特性，脉动幅值逐渐增强。

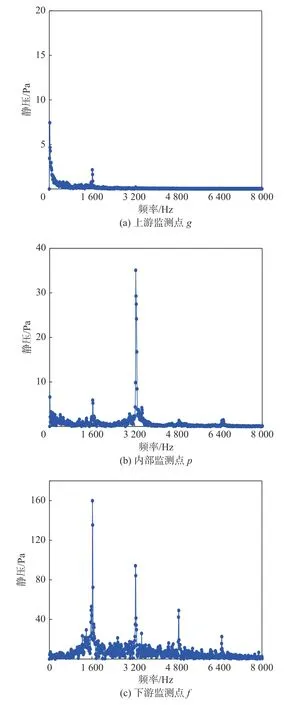
图12 沟槽上、下游压强脉动频谱Fig.12 Pressure fluctuation spectrum at the upstream and downstream of the groove

表5 给出了α=6°、h/λ=0.35 时，不同相对位置沟槽上、下游监测点g、p、f的压强脉动主频及对应幅值。表6 则为α=6°、x/c=0.65 时，不同相对深度沟槽上、下游压强脉动主频及对应幅值。可知，不同参数沟槽的存在对其翼型表面上、下游压强脉动的影响，其频率呈现类似图12的特性，沟槽内部监测点p的压强脉动主频表现为上、下游主频的2 倍，说明沟槽内部二次涡产生、发展和脱落过程始终存在。沟槽结构的存在对上游监测点g的压强脉动幅值几乎没有影响。在不同相对位置下，随弦向的增加，沟槽内部监测点p脉动幅值逐渐增加，但沟槽下游监测点f幅值却呈减小趋势。在同一位置，随沟槽相对深度的增加，沟槽内部监测点p脉动幅值逐渐增加，下游监测点f幅值呈先增大后减小趋势，在h/λ=0.35 时出现最小值。

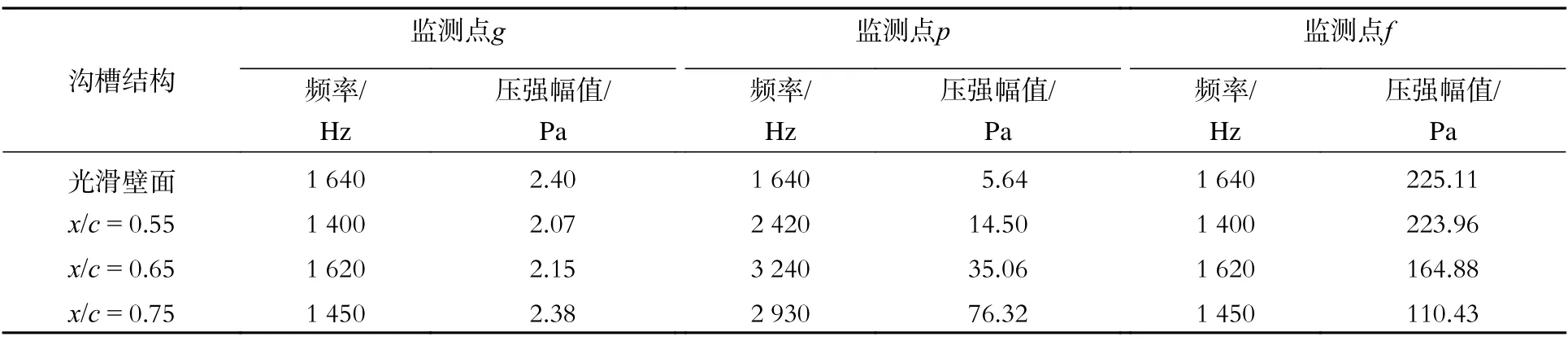
表5 不同相对位置沟槽上、下游压强脉动主频及对应幅值Tab.5 Main frequency and the corresponding amplitude of pressure fluctuationat the upstream and downstream of the groove at different relative positions

表6 不同相对深度沟槽上、下游压强脉动主频及对应幅值Tab.6 Main frequency and the corresponding amplitude of pressure fluctuationat the upstream and downstream of the groove at different relative depth

3 结 论

本文以NACA510 翼型沟槽结构为研究对象，通过大涡模拟方法对翼型绕流流场进行了数值计算，分析了沟槽结构对翼型气动特性与涡流结构的影响规律，取得了以下结论：

（1）在小攻角下，沟槽表面对翼型的升、阻力系数影响很小，大攻角下升、阻力系数明显减小，沟槽位于x/c=0.65、相对深度h/λ=0.35时，翼型阻力系数的减小量大于升力系数的减小量。

（2）沟槽结构的存在改变了下游涡脱落情况，对上游影响不明显。6°来流攻角下，随弦向方向，沟槽下游监测点f压强脉动幅值逐渐减小；随沟槽深度的增加，监测点压强脉动幅值呈先降后增的分布趋势，在h/λ=0.35 时达到最小。沟 槽 较 浅(h/λ=0.10、h/λ=0.20、h/λ=0.35)时，沟槽的存在对频率的影响不明显；沟槽达到一定深度(h/λ=0.50、h/λ=0.80)后，压强脉动频率发生突变，频率明显降低。

（3）气体流经沟槽结构时会在沟槽内部形成反向二次涡，其压强脉动主频为上、下游主频的2 倍。在一定条件下，沟槽内部涡流失稳，存在周期性涡流产生、发展和脱离。气体流经沟槽结构，翼型尾缘保持了上游及沟槽内部压强脉动的频率特性，脉动幅值逐渐增强。