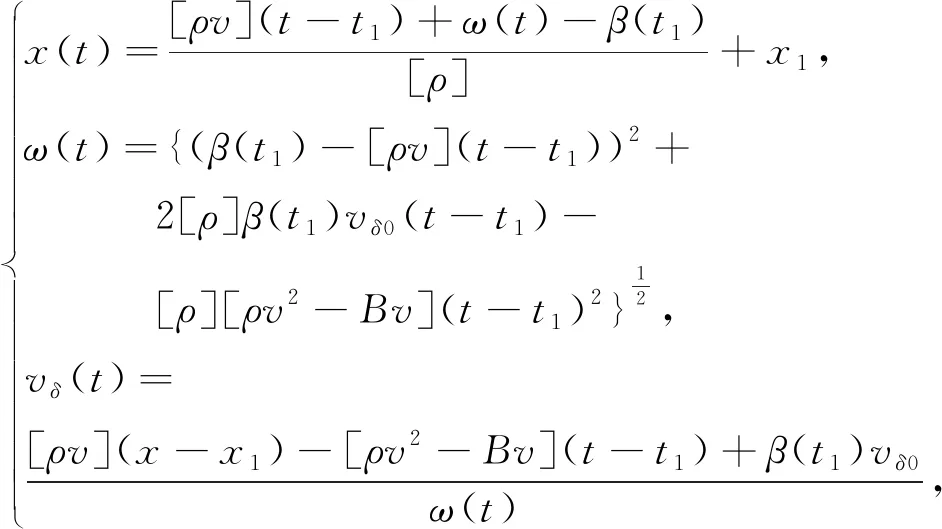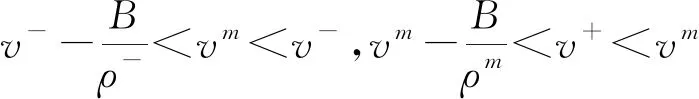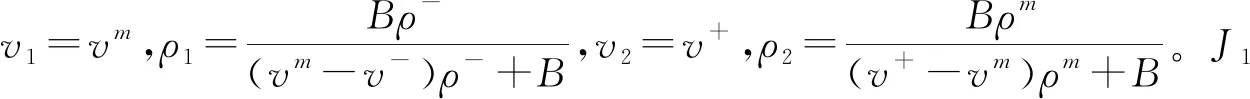Aw-Rascle交通模型的初值问题
张得霞,潘丽君
(南京航空航天大学理学院,江苏 南京 211106)
本文研究Aw-Rascle(AR)交通模型[1]
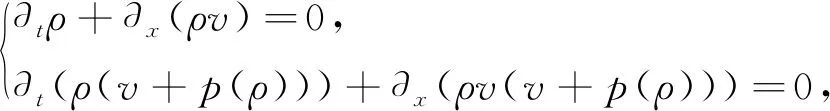
(1)
其中,ρ≥0,v≥0,p(ρ)分别表示t时刻x位置处的汽车密度、速度和压力。2000年,AW和RASCLE建立了上述模型,它修正了由DAGANZO[2]提出的二阶模型在交通流中存在的问题。 AR模型是描述单向道路的交通流模型,常用来解释交通拥堵等现象[3],有关AR模型的研究,可参考文献[1,4-5]。
对于AR模型,AW和RASCLE提出压力项p=ργ,γ>0。 最初,CHAPLYGIN[6]、TSIEN[7]和VON KARMAN[8]用压力
p=-ρ-1
(2)
来近似飞机机翼的上升力。 2013年,PAN和HAN[9]采用状态方程

(3)
研究AR模型的初边值问题。 SHAO和HUANG[10]采用分离delta函数法研究模型(1)和(2)的相互作用问题。 需注意到,文献[9-10]中都出现了delta解。 Delta激波具有超压缩性,能够描述车辆的汇聚过程,解释交通的某些极端情形[11]。 关于delta激波的研究可参考文献[4,12]等。 本文将文献[9]的方程(3)推广到更一般形式
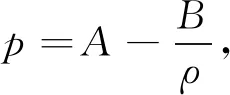
(4)
其中A为任意常数,B>0。我们将构造出模型(1)和(4)的黎曼解,并分析当A→0时,黎曼解的渐近性态。 此外,讨论AR模型的相互作用问题。
本文安排如下:在第1节中,介绍模型(1)和(4)的基础知识,求解模型的黎曼问题
(v,ρ)(x,0)=(v±,ρ±),±x>0,
(5)
其中常数v±,ρ±>0。在第2节,采用特征分析的方法,研究AR模型初值为三片常数的相互作用问题,得到了4种不同结构的解。
1 带有Chaplygin项的AR模型的黎曼解
这一节,主要讨论模型(1),(4)和(5)的黎曼问题。将式(4)代入方程组(1)得
方程组(6)的特征值及特征向量为

(7)
接下来求有界间断解ξ=σ。方程组(6)的Rankine-Hugoniot条件为
(8)
其中[ρ]=ρ+-ρ-,求解得到接触间断J,接触间断压缩波S(简称压缩波S),
J(v-,ρ-):v=v-=σ,
(9)

(10)
由式(7)和(10)知,稀疏波曲线与压缩波曲线重合。
将曲线(7),(9)和(10)在(v,ρ)平面表示出来。平面被分为3个区域:
III={(v,ρ)|v>v-}。
根据右状态(v+,ρ+)的位置,下面构造黎曼问题(5)和(6)唯一显式整体解。

但是,如果(v+,ρ+)∈I,此时方程组(6)的黎曼问题具有如下形式的delta解
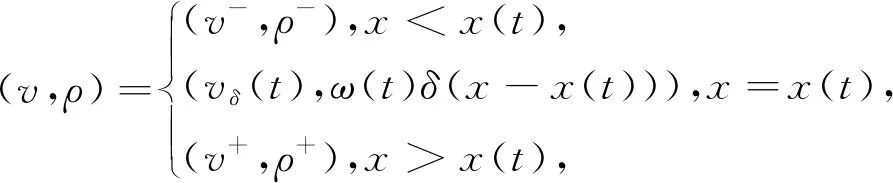
(11)
其中,x(t),vδ(t)∈[0,∞),δ(·)表示delta测度。x(t),vδ(t),ω(t)分别表示Sδ波的位置、速度和权。测度解(11)满足下面的广义Rankine-Hugoniot条件,

(12)


(13)
只证明式(13)的第二个等式,第一个等式可以类似证明。
(ρv2+Aρv-Bv)φx)dxdt=
((ρv2+Aρv-Bv)φ)x)dxdt-
(ρv2+Aρv-Bv)x)dxdt+

((ρv2-Bv)φ)x)dxdt+

求解带有如下初值的常微分方程组(12),
x(0)=0,ω(0)=0,
(14)
得到
(x(t),vδ(t),ω(t))=

(15)

(x(t),vδ(t),ω(t))=

(16)
可以发现
通过计算有
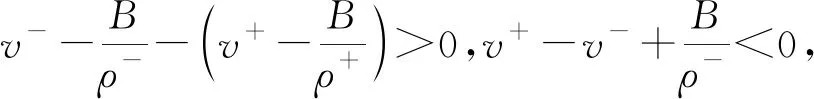
因此,(v+,ρ+)∈I时,黎曼解为(v-,ρ-)+Sδ+(v+,ρ+)。综上我们得到:
定理1 黎曼问题(5)和(6)存在唯一的显式黎曼解,且当式(11)中A→0时,黎曼解的结构保持不变。
注1我们将状态方程(3)推广为(4),但AR交通模型黎曼解结构不发生变化。
2 波的相互作用
这一部分主要研究模型(6)和(4)的三片常数的初值问题,
(17)
其中ε为任意给定常数。
根据从(-ε,0)和(ε,0)处发出的接触间断与delta激波的类型,将情况分为以下几种,其中我们只对ρ+≠ρ-的情况进行详细分析,ρ+=ρ-情况类似讨论。
通过前一部分的分析可以知道,若t足够小,初值问题(6)和(17)的解结构为
(v-,ρ-)+Sδ1+(vm,ρm)+Sδ2+(v+,ρ+)。
Delta激波Sδ1和Sδ2的速度分别为vδ1,vδ2,且
其中
ωδ1(t)=
ωδ2(t)=
由于vδ1>vδ2,那么在一定时间内,Sδ1会追上Sδ2,交点(x1,t1)满足
(18)
x(t1)=x1,ω(t1)=β(t1),vδ(t1)=vδ0。
(19)
其中,
β(t1)=ωδ1(t1)+ωδ2(t1),
显然vδ2 (20) 综上讨论,当t>t1时,问题(6)和(17)解的结构为(v-,ρ-)+Sδ3+(v+,ρ+),如图1所示。 图1 两个delta激波发生相互作用 注2Delta激波Sδ1,Sδ2的传播速度为常速,但delta激波Sδ3的传播速度为变速。 当t很小时,问题(6)和(17)解的结构为 (v-,ρ-)+S1+(v1,ρ1)+ J1+(vm,ρm)+Sδ1+(v+,ρ+)。 (21) 综上所述,当t1 图2 接触间断与delta激波发生相互作用 (v-,ρ-)+S1+(v1,ρ1)+ S2+(v2,ρ2)+J2+(v+,ρ+)。 当t很小时,问题(6)和(17)的解为 (v-,ρ-)+S1+(v1,ρ1)+J1+(vm,ρm)+ S2+(v2,ρ2)+J2+(v+,ρ+)。 wave 图3 两个接触间断发生相互作用 当t很小时,相互作用问题(6)和(17)的解结构为 (v-,ρ-)+Sδ1+(vm,ρm)+S1+ (v1,ρ1)+J1+(v+,ρ+)。 通过上述讨论,得到了delta激波与接触间断以及接触间断之间相互作用的结果,结论如下: 定理2 相互作用问题(6)和(17)存在唯一的整体显式解,delta激波与接触间断相互作用后会导致delta激波的速度由常速变为变速。