随机多面骨牌链基尔霍夫指标的数学期望
吴廷增,蔚 勇
(青海民族大学数学与统计学院,青海 西宁 810007)
令G是一个图, 其顶点集为V(G), 边集为E(G)。 图G的顶点集和边集的大小分别为|V(G)|=p, |E(G)|=m。v∈V(G)的邻集, 记为NG(v), 是指在G中与v相邻的所有的点组成的集合。 本文考虑的所有图均为连通图, 未定义的概念和符号参见文献[1]。
连通图G的2个顶点i和j间的电阻距离记作rij或r(vi,vj), 定义为通过用单位电阻来代替G中每条边而构造出的电网络N中的节点i和j之间的有效电阻的阻值,且满足欧姆定律。 图G的基尔霍夫指标Kf(G) 定义为G中所有顶点对之间的电阻距离之和[2-4], 即
其中r(vi|G)表示顶点vi与G中所有其他顶点的电阻距离之和。图的基尔霍夫指标被广泛研究,参见文献[5-9]。一个多面骨牌图(也称棋盘[10]或正方细胞构形[11])是指平面上2个全等且边长为1的正方形按照要么无公共顶点要么有一条公共边的规则排列而得的连通几何图形。 多面骨牌图在统计物理和结构化学中有广泛的应用。一个包含n个正方形的多面骨牌链Qn是嵌入在多面骨牌图上的子结构[12]。多面骨牌链Qn可以看作是由具有n-1个正方形的多面骨牌链Qn-1通过一条割边连接一个新的正方形而得,见图1。

图1 包含n个正方形的多面骨牌链Qn
本文探讨随机多面骨牌链基尔霍夫指标的数学期望以及期望的极值情况。
1 前期准备
令Qn=S1S2…Sn是包含n(≥2)个正方形的多面骨牌链, 其中Sk看作是Qn中的Sk-1通过割边uk-1wk连接的第k个正方形构成(k=2,3,…,n),wk=v1是正方形Sk的一个顶点。 对于Sk中的一个顶点v, 如果v和wk的距离为1, 则称v为邻位顶点,记作ok;如果v和wk的距离为2, 则称v为对位顶点, 记作pk; 观察图1, 不难发现Sn中wn=v1,on=v2和v4是邻位顶点,pn=v3是对位顶点。
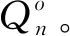

图2 随机多面骨牌链所有的嵌入方式


图3 多面骨牌链中的2种局部排列
一个包含n个正方形的随机多面骨牌链Q(n,t)是通过逐步增加末端正方形得到的多面骨牌链。 在每一步k(=3,4,…,n)中, 都有可能随机选择下面2种结构:

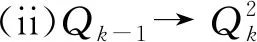

2 主要结果
下面我们来计算包含n个正方形骨牌的随机多面骨牌链基尔霍夫指标的数学期望。

证明由随机多面骨牌链的定义可知,Qn是由Qn-1通过一条割边连接一个新的正方形骨牌构成, 这里设其末端的正方形顶点集为{v1,v2,v3,v4} 及新增的关联边记为un-1v1(图1)。 由电阻距离计算公式得
右边4个顶点v1,v2,v3,v4与Qn-1中任意一点v关系如下:
r(v1,v)=r(un-1,v)+r(v1,un-1),
r(v2,v)=r(un-1,v)+r(v2,un-1),
r(v3,v)=r(un-1,v)+r(v3,un-1),
r(v4,v)=r(un-1,v)+r(v4,un-1),
且对于Qn-1中的4(n-1)个顶点,有
r(v1|Qn)=r(un-1|Qn-1)+
(1)
r(v2|Qn)=r(un-1|Qn-1)+
(2)
r(v3|Qn)=r(un-1|Qn-1)+
(3)
r(v4|Qn)=r(un-1|Qn-1)+
(4)
其中, 下面结果通过观察图1是很容易得知的:
r(v1,un-1)=1,
r(v3,un-1)=1+1,
代入式(1)—(4)得
r(v2|Qn)=r(un-1|Qn-1)+
r(v4|Qn)=r(un-1|Qn-1)+
且知道
所以
Kf(Qn-1)+4r(un-1|Qn-1)+26(n-1)+5。
(5)
如图3,其末端正方形骨牌是通过吸附邻位顶点或对位顶点以下2种情形实现。


对于一个随机多面骨牌链Qn(n,t),r(un|Qn)是一个随机变量,将其数学期望记作
Un=E(r(un|Q(n,t,))),
以上2种情形分别以概率t,1-t随机实现,则
(6)
对于式(6), 由数学期望运算性质及E(Un)=Un得
Un-1=Un-2+[7t+8(1-t)](n-1)-
Un-2=Un-3+[7t+8(1-t)](n-2)-
……
累加得
(7)
又因为随机多面骨牌链的基尔霍夫指标的期望的递推式已经由式(5)给出,由数学期望性质及式(7)得
E(Kf(Q(n,t)))=
E(Kf(Q(n-1,t)))+
E(Kf(Q(n-1,t)))=
E(Kf(Q(n-2,t)))+
E(Kf(Q(n-2,t)))=
E(Kf(Q(n-3,t)))+
……
E(Kf(Q(2,t)))=
E(Kf(Q(1,t)))+
得随机多面骨牌链基尔霍夫指标的数学期望为
定理1对于一个随机多面骨牌链Q(n,t)(n≥3), 有
证明由引理1结果知,
E(Kf(Q(n,t)))=
注意到,当n≥3时,



