正则图的Q-图的(度)基尔霍夫指标
李佳建
(兰州交通大学 数理学院, 甘肃 兰州 730070)
本文只考虑简单无向图,设G=(V(G),E(G))是n个顶点、m条边的连通图。图G的顶点i与顶点j之间的电阻距离[1],是指以单位电阻代替G中每条边后构造出的电网络中节点i与j之间的等效电阻,记为Ωij。
图的电阻距离与通常的距离相似,是在图上定义的一种新的距离函数。因此,与基于距离的图不变量类似,定义了基于电阻距离的各种图不变量,其中,最著名的是基尔霍夫指标,也称为总有效电阻,用R(G)来表示,定义为所有顶点对之间的电阻距离之和[2-4],即
近年来,研究人员对这一指标给予了较多的关注,将其拓展引入了两种新的指标,其中一个是乘法度-基尔霍夫指标[5]:
另一个是加法度-基尔霍夫指标[6]:
这里ri表示图G中顶点i的度。
图G的线图,记作l(G),是指以图G的边集为顶点集,l(G)的两个顶点相邻当且仅当对应的G的两条边在G中相邻。图G的Q-图,记作Q(G),是指在图G的每条边中插入一个新顶点,然后把邻接的边对应的新插入顶点相连接而得到的图,图1给出了图G,l(G)、Q(G)的示例。
文献[7]研究了剖分图的基尔霍夫指标,文献[8]给出了Q-图的电阻距离,文献[9]给出了正则图的线图的电阻距离,文献[10]得到了剖分图、三角剖分图的基尔霍夫指标以及加法度-基尔霍夫指标和乘法度-基尔霍夫指标,文献[11-12]分别刻画了G与l(G)和G与Q(G)它们的基尔霍夫指标之间的关系。此外,还有一些关于其它图的度-基尔霍夫指标的相关结果[13-15]。
受上述文献的启发,这里主要讨论正则图G的Q(G)图的(乘法度或加法度)基尔霍夫指标与l(G)的基尔霍夫指标之间的关系。

(a) G (b) l(G) (c) Q(G)图1 图G及其Q(G)
1 预备知识

引理1.1[8]设图G是一个有n个顶点、m条边的r-正则图,则


(3)当i,j∈V(i≠j)且Г(i)={e1,e2,…,er},Г(j)={f1,f2,…,fr}时,有
引理1.2[16]设图G为n阶连通图,那么所有相邻顶点间的电阻距离之和为n-1,即
2 主要结果
定理2.1 设图G为具有n(n≥2)个顶点、m条边的r-正则连通图,则
证明由基尔霍夫指标定义,有
(1)
首先,由引理1.1(1)知
(2)
其次,由引理1.1(2)知
(3)

(4)
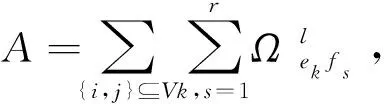
(5)

由引理1.2知
(m-1)(n-1)/[r(r+1)],
(6)
因此,由式(4)、(5)、(6)可得
(7)
结合式(1)、(2)、(3)、(7),定理得证。证毕。

下面给出Q(G)的加法度或乘法度-基尔霍夫指标与l(G)的基尔霍夫指标之间的关系。
定理2.2 设图G为n≥2个顶点、m条边,r-正则的连通图,则
证明由加法度-基尔霍夫指标的定义,有
下面计算等式右边的3个部分。
(1)对于第一部分,由引理2.1知

由式(2)知
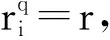
综上所述,定理2.2得证。
定理2.3 设图G为n≥2个顶点,m条边,r-正则的连通图,则
证明由乘法度-基尔霍夫指标的定义,有

证毕。

