FDM快速成形工艺参数的多尺寸目标优化
高善平,顾立志
(1.泉州信息工程学院 机械与电气工程学院, 福建 泉州 363000;2.华侨大学 机电及自动化工程学院, 福建 厦门 361021)
熔融堆积成形(Fused Deposition Modeling,FDM)是增材制造的主要工艺之一,该技术将计算机图形学、复杂系统与数字控制技术、材料科学、光机电一体化技术等先进技术集于一体,克服了传统制造工艺的局限性,充分体现制造的柔性化和高效化[1]。该技术可以大大缩短新产品开发周期,有效节省开发成本,提高企业快速响应市场的能力,从而提高市场竞争力[2]。目前,马杰[3]提出了一种改进的挤出丝截面模型以及相应的轮廓偏置算法,对成形零件的表面精度进行了优化;李金华等[4]针对FDM成形中的翘曲变形现象,对多目标下的工艺参数优化进行了研究;还有部分科研团队从成形角度和层厚参数的角度进行研究,提出了相应的数学模型,可预测零件的成形尺寸[5]。但是,FDM成形精度仍然不能满足用户对快速制造的需求,如何获得一套稳定的工艺方案是解决该问题的关键。
1 熔融堆积成形质量的影响因素
FDM成形的基本过程包括:三维实体模型的数据处理,对数据模型的离散,对二维数据进行轨迹规划,再进行插补、堆叠形成三维实体。FDM成形工艺涉及数字化设计、数字控制、材料成形、工艺规划及后处理等方面内容,每个环节都会产生误差甚至导致成形件报废。分析FDM成形工艺的误差及影响因素,需要考虑成形工艺的整个过程。结合文献与笔者的前期研究成果[6],归纳出FDM成形质量的影响因素构成如图1所示。

图1 影响FDM成形质量的主要因素
2 成形件尺寸精度的试验研究
由于受到FDM工艺的成形原理以及材料性能等条件的约束,目前还没有一种全面稳定的方案可以保证成形精度。本文通过试验,以成形精度为目标分析主要参数对成形精度的影响机理。
2.1 丝宽对尺寸精度的影响及修正的丝宽补偿公式
FDM工艺在进行产品打印时,喷头挤出的丝材以物理形态存在,为实体尺寸,而数据模型的尺寸趋近于0,必然使成形件的尺寸偏大,在研究过程中就必须考虑理论轮廓线引进的误差,还要考虑丝材从挤出到成形的过程中发生的收缩变化。杨丽[7]推导出了热收缩量和分子取向收缩量的数学模型,并明确了从X-Y方向和Z方向收缩量的区别(X为横向水平方向,Y为纵向水平方向,Z为竖直方向)。以上热收缩量和分子取向收缩量对应的数学模型理论上可以准确获得丝宽的补偿量,但在实际生产过程中,必然存在不定因素的影响和多因素的交叉影响。本文基于丝宽变动理论公式,通过试验,总结归纳出一定成形方向的成形过程时,尺寸精度的变化规律,回溯丝宽变动误差补偿,以减小乃至消除其影响,构建的丝宽补偿公式为
(1)

2.2 成形方向对尺寸精度的影响

图2 尺寸误差与成形角度的关系
为了验证成形角度对尺寸精度的影响,将试验件模型分别在0°、30°、45°、60°、90°的成形方向进行成形。层厚参数取0.2 mm,材料为聚乳酸(Poly Lactic Acid,PLA),其他工艺参数由系统推荐。为避免引入其他因素产生的误差,将成形件在25 ℃环境中放置24 h,然后用千分尺测量制件的长宽高,计算尺寸误差,并绘制绝对尺寸误差-成形角度曲线图,如图2所示。
由图2综合分析,可得出如下结论:
(1)当成形方向改变时,成形件X、Y、Z方向的尺寸与热床的方位发生变化,其尺寸误差随之变化。尺寸误差由大到小依次为ΔX>ΔZ>ΔY,其中X方向的尺寸最大,Z方向尺寸最小;误差随着尺寸变大而增大,而ΔZ却比ΔY大一些,主要原因有两点:一是在切片处理时将三维数据模型分割为二维轮廓数据,每个切片层之间部分轮廓信息丢失,产生间隙,且分层时一般采用平行于热床的面,从而引入了模型在Z方向的误差;二是FDM成形时,丝材是熔融挤出并堆叠,经过冷却后形成实物模型,这一过程如果喷头和环境的温度差无法使丝材在堆叠时刚好处于冷却稳定状态,就会由于重力和层与层之间的挤压,使得Z方向的误差逐步叠加。
(2)无论是哪个方向的尺寸,当成形角在0°和90°时尺寸误差最小,而在两者之间误差会随角度的变化而发生改变。当成形角为0°或90°时,成形件表面出现的是等高的丝材轨迹,而其他成形角成形时出现了阶梯效应。图2显示在(0°,90°)区间内存在某角度α,当θ<α时,尺寸误差随θ的增大而增大;在θ>α时,尺寸误差随θ的增大而减小,这与台阶误差的变化相似。由此可见,α角的范围为60°度左右,是成形过程中是否添加支撑的参考,也正因为引入了支撑导致支撑剥落时尺寸精度受到了影响,另一方面也会因为成形角度的变化而导致阶梯效应发生变化,从而影响尺寸精度。
3 FDM成形件的尺寸精度工艺优化研究
由于工艺参数对成形件尺寸精度的影响存在差异性,本文选择层厚、填充率、打印温度、打印速度4个主要工艺参数,通过田口试验探究各因素对制件尺寸精度的影响程度,通过理论与试验的比较分析,确定最佳优化措施。
3.1 试验方法
3.1.1 田口试验方法
从试验成本和精度等方面综合考虑,采用田口方法进行试验。田口方法习惯把信噪比(S/N)作为产品质量稳定性的评价指标,对于研究产品特性是越小越好的,则S/N越大越好,该特性在田口方法中,称为望小特性[8]。这里研究的产品特性是尺寸误差,则越小越好,最优值为0,所以本试验选择望小特性来评价产品的误差值。
望小特性的评定函数[8]为
(2)
式中n为试验次数,Δyi为样本尺寸的平均误差。
本试验的目的是分析成形件的尺寸精度,则把成形件各测量要素的尺寸误差作为目标,测量的误差值用相对误差来描述,公式为
(3)
式中y理为理论值,y实为实际值。
3.1.2 成形件尺寸精度的试验流程
运用田口方法设计的试验流程如下:
(ⅰ)分析导致FDM成形产品出现尺寸误差的控制因子,确定评估尺寸误差的可行性条件;
(ⅱ)分析并选取该试验的品质特性y和目标函数f(y);
(ⅲ)分析并确定可控因子,参照设备性能选定各因子水平,设计正交表;
(ⅳ)在稳定的条件下进行正交试验;
(ⅴ)分析各控制因子的极差及方差,预测单目标下各工艺参数的最佳组合;
(ⅵ)通过验证性实验,分析得出最佳水平。
3.2 试验设计
3.2.1 试样模型设计与试验参数选择
为了既能保证试验可靠性又能节省试验成本,本文设计了试件模型(图3),选取层厚、填充率、打印温度和打印速度4个参数作为主要控制因子,分析它们对成形件尺寸精度的影响。

图3 试验件三维数字模型
3.2.2 正交试验设计
由于打印设备自身的精度及工艺原理的原因,在此不考虑控制因子相互之间的交叉影响。根据Cura软件以PLA为打印材料所推荐的FDM成形工艺参数(层厚0.1~0.2 mm、打印温度195~215 ℃、热床温度50 ℃、打印速度<80 mm/s、填充率>20%),确定3个水准和4个控制因子的试验最适合,正交试验表L9(34)见表1。

表1 正交试验表
本文选取了4个参数对成形精度的影响作为研究对象,其余参数根据Cura切片软件的默认值、3D打印机硬件配置及材料参数进行设置。
3.2.3 试验数据统计
本试验在相同的环境下,选择热床的最佳加工区域,随机加工出9个合格试验件,并置于室温环境下24 h,采用千分尺测量尺寸。为了保证测量结果准确、可靠,每个尺寸在不同方位测量3次取平均值,作为最终的试验数据。
3.3 基于正交试验的单目标参数的优化与分析
取各试件同一个测量要素的尺寸误差作为评价特性。长度、高度及圆柱凸台直径3个几何尺寸的相对误差分别用ΔX、ΔZ、ΔL表示。
3.3.1 加工参数对尺寸精度的影响
根据测量的尺寸误差求得信噪比(S/N),结果如表2所示,由表中数据可知,X、Z、L三要素的平均误差分别为0.448%、1.647%、-0.114%,ΔZ最大,ΔX最小,Z向尺寸小于实际值。运用Minitab绘制4个控制因子与其3个水准的极差图,如图4所示。

图4 尺寸误差信噪比极差图
由图4可知,4个控制因子的不同水准对产品X、Z、L尺寸误差产生的影响也不同;保证X、Z、L三要素尺寸精度的最佳工艺参数组合分别是A3B3C2D1、A2B1C3D2、A2B1C2D2。由此可见,影响各要素几何尺寸精度的最优工艺参数组合是不同的,如果在加工过程中只要求单个尺寸精度,可以选用对应的最优工艺参数组合方案。
为了深入了解单个因子对单目标的影响程度,利用Minitab软件对单目标下各控制因子进行方差分析,结果如表3所示。

表3 X、Z、L尺寸控制因子的方差分析结果
表3的分析主要是通过获得F值来判断控制因子对单目标的影响程度,F值越大,说明该控制因子影响程度越大。因此,所选控制因素对ΔX、ΔZ、ΔL的影响程度大小排序结果分别为B>A>D>C、C>D>B>A、A>B>C>D。在4个控制因子中,层厚影响最显著,另外,填充率太高则会使尺寸误差变大。
3.3.2 尺寸误差预测和补偿方程
根据前文分析,在FDM成形过程中,不同几何要素的成形面尺寸受到不同因素的影响,主要包括喷头误差、材料收缩误差、分层误差、打印速度等,它们对成形尺寸精度的影响都比较大,因此,应该对误差给予相应的补偿[9]。理论模型是在特定条件下推导而成的,存在一定的误差,根据前文研究,单因素下的误差由理论模型进行补偿,比如材料收缩导致的误差采用收缩公式补偿,并未将成形件的形状、尺寸以及工艺参数和成形时间等考虑进去,并且它们之间还存在交互作用,要获得准确的补偿比较困难。通过各因子的贡献度分析,分别求出3个要素尺寸误差的回归方程,并预测产品在X、Z方向和圆柱凸台直径的尺寸误差。3个要素尺寸的误差补偿方程分别为
ΔX=0.78-0.52h-0.006 63v+0.000 82T-0.000 67η,
(4)
ΔZ=3.09+0.54h+0.004 62v-0.008 10T-0.005 13η,
(5)
ΔL=0.24-1.37h+0.001 50v+0.000 10T,
(6)
式中h为成形后单层丝的厚度(mm),v为喷头扫描速度(m/s),T为喷头温度(℃),η为填充率(%)。
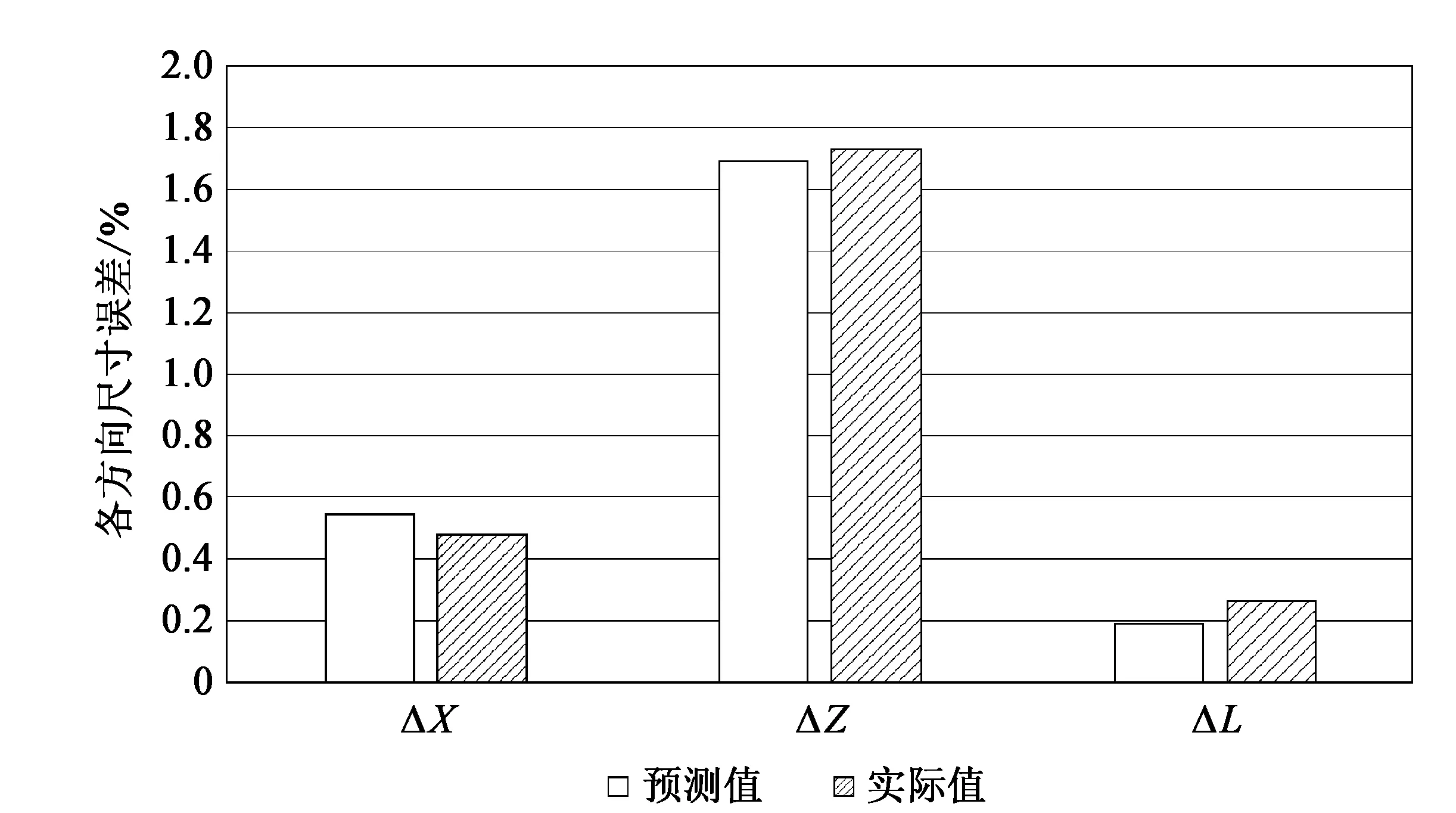
图5 单目标尺寸的实际值与预测值对比
由补偿方程可知,各控制因子对水平、竖直和圆柱直径等不同要素尺寸的影响是不一样的,且存在不同程度的关联性。
为了验证回归方程的合理性,我们选用第一组试验参数所成形制品的误差与预测值进行比较,并绘制柱状图(图5)。可见X、Z方向和圆柱凸台直径的尺寸误差的实际值与预测值相差甚小,3个尺寸中最大的误差差值仅有0.07%,说明以上推论所得的误差回归方程是合理的。
3.4 多目标优化下的成形工艺参数分析
前文的研究中获得了不同要素尺寸的最优成形工艺参数的水准组合,但最优工艺参数水准组合只对其单一尺寸起到相对较好的作用,用于其他尺寸却未必可行,而在实际加工中,一个零件加工一次仅能设置一组参数,所以需要探索一套能满足多类型尺寸的最优工艺参数组合。本文运用灰系田口方法对试验数据进行关联性分析,探索同一个零件多种几何要素尺寸精度的最佳工艺参数组合方案。
3.4.1 灰关联分析
灰关联分析法是通过不同要素之间的灰关联度来衡量不同因素之间的关联程度的一种分析方法。其本质在于将试验数据转化成曲线图并对多个曲线图进行比较,获得其关联度信息,曲线相似度越高,关联度就越大。灰系田口法是将田口方法与灰关联分析法相结合,进行系统多目标优化的一种研究方法[10-11],其关系如图6所示。

图6 田口方法及灰系田口方法流程关系图
3.4.2 基于灰系田口方法的参数优化
3.4.2.1 灰生成系列
在灰关联分析之前,需要将相关试验数据转化成具有相同量纲或数量级的数值。本试验中的序列是空间序列,需要对ΔX、ΔZ、ΔL的信噪比无量纲化处理,令Xi为生成序列集,xij为生成序列,则量化公式为
(7)
其中yij为第j个水准下的第i次试验;i=1,2,3,…,9;j=1,2,3。
3.4.2.2 灰关联系数
由于本试验分析的对象是尺寸误差,一般来说误差数值越小越好,因此采用望小特性进行分析,取数值0作为参考系列,即
X0=(x01,x02,…,x0j,…,x0n)=(0,0,…,0,…,0),
(8)
推导出Xi系列与参考数列的比较关系式为
(9)
结合以上公式,经过计算获得灰关联系数。
3.4.2.3 灰关联度
根据关联度计算公式,推导出Xi系列与参考数列的关联关系计算公式为
(10)
其中ωj表示指标的权重系数,通常根据工作领域不同及实践总结由操作者决定,若一个对象包含多个指标,则各指标权重系数之和为1。根据各尺寸的重要性及可控性,这里X、Z、L的尺寸精度的权重分别取0.35、0.3、0.35。获得灰关联度的计算结果见表4。
3.4.2.4 灰关联度分析
将3个目标尺寸转化成具有相关性的灰关联度值,然后对该灰关联度值进行极差和方差分析,判定控制因子的水平及显著程度,如图7和表5所示。

图7 灰关联度的极差分析

表4 灰关联度的计算结果

表5 各因子灰关联度的方差分析
分析以上数据,获得多尺寸目标优化下的最优成形工艺参数组合为A1B2C1D1,即在分层厚度0.15 mm、喷头扫描速度70 m/s、喷头温度205 ℃、填充率30%时,得到最优尺寸,影响较显著的是层厚。
根据上述分析推导出9个试件的灰度预测值的补偿方程为
ΔXZL=-0.47+1.329h+0.001 38v+0.003 43T+0.109η,
(11)
式中ΔXZL为S/N的灰关联度预测值。

图8 灰度S/N的预测值与真实值曲线图
绘制S/N灰关联度的预测值与实际值折线图(图8)并进行比较,可知两条曲线变化基本一致,多数预测值产生的误差不大,均在3%以内。
4 总结
本文主要分析了FDM成形过程中可能产生的各种误差,探索了FDM成形工艺中产生尺寸误差的主要原因,提出对应策略。
通过多工艺参数优化组合研究,取得了以下成果:
(1)FDM成形过程中出现的误差可以归纳为3类:原理性误差、成形过程误差(动误差)和后处理误差。
(2)进行了四因素三水平正交试验研究和回归分析,获得单尺寸目标下的最佳工艺参数组合及控制因子的显著程度,并推导出了3种不同要素尺寸的误差回归方程。
(3)获得了不同要素尺寸的多目标最优工艺参数组合及各控制因子的影响显著程度,推导出了3个不同要素尺寸误差信噪比的灰关联度预测值的回归方程,并通过试验验证了其合理性,从而推导出可实现多工艺参数优化的工艺规程。
(4)层厚和喷头温度对FDM成形精度的影响较大,层厚并非越小越好,喷头温度也应根据需要选取不同值;打印速度对尺寸精度的影响有驼峰性;填充率对成形尺寸精度影响不显著。

