基于边缘计算的交叉路口无人驾驶车辆通行轨迹预测算法

郝璐璐，谢 辉，宋 康，闫 龙

（内燃机燃烧学国家重点实验室，天津大学，天津300072，中国）

随着车辆保有量的迅速增加，城市交叉路口拥堵问题、安全问题、节能与环境问题已经成为全社会聚焦问题。在智能网联的背景下，清华大学的徐彪[1]等人提出基于遗传算法和分支定界算法的通行车速计算提高车辆在路口的通行率，北京理工大学的邹渊[2]等人将有效通行时间的信号灯模型与伪谱法结合降低车辆在路口的能耗，长安大学的徐婷[3]等人提出基于车对万物 (vehicle to everything，V2X)的驾驶员辅助系统对车辆换道行为预测提高车辆在路口的安全性。在现实情况中，普通车辆没有搭载感知通信设备，部分驾驶员存在转弯不打转向灯等违规操作，单个智能车辆在交叉路口感知范围受限且无法提前获取路口其他车辆的信息。这种情况下在智慧道路的路端对交叉路口附近车辆进行准确的轨迹预测，既可以解决城市交通问题，也可以将预测的轨迹信息传递给智能车辆，作为智能车辆轨迹规划的先验信息，辅助完成车路协同规划。

目前车辆轨迹预测方法主要分为3大类别：第1种：基于物理机理的预测模型。在该方法中，车辆被视为二维平面内受物理规律控制的物体，通过速度、加速度、位置、轴距、质量等参数的数学关系建立车辆的动力学或运动学模型进行轨迹预测[4]。M. Brannstrom等人[5]为了提高计算效率将车辆动力学模型简化为自行车模型，A. Houenou等人[6]建立了Descartes坐标系下的车辆状态矩阵用来表示车辆运动学模型。但是该方法没有考虑驾驶员自身的特性以及车辆行驶环境的变化，因此只能在短时间内保持预测准确性，随着时间的增加误差逐渐增大。

第2种：基于驾驶员意图的预测模型。它主要分为回归模型和分类模型，其中回归模型在驾驶员意图不明时倾向于输出所有训练轨迹的均值，分类模型虽能获取驾驶员意图但是却无法获取车辆具体的轨迹。XIAO Wei[7]等人利用车辆历史轨迹与车道线之间的时间与空间关系来进行机动识别，随着环境复杂度增加，驾驶员意图的识别分类困难会显著增加，运算效率降低，同时也忽略了环境因素如交通信号灯和交通规则等外部影响因素存在，这种影响在交叉路口影响显著。

第3种：基于交互作用的预测模型。FENG Xidong等人[8]利用嵌入生成对抗网络GAN来预测车辆未来的轨迹，随着环境复杂度增加，模型运算的复杂度也随之增加难以满足实时性的要求，而且不能够充分考虑交通环境的不确定性。车辆边缘计算 (mobile edge computing，MEC) 的提出与应用，可改善无人驾驶车辆的时延问题、运算问题及散热问题[9]。WU Gaoxiang等人[10]提出移动边缘计算框架以降低无人机的终端负载和能耗。O. Bekkouche 等人[11]通过在边缘计算平台中收集处理数据降低时延，并在边缘计算平台中处理路径规划算法改善网络资源配置。

本文针对交叉路口固定的道路拓扑结构和交通规则，提出基于支持向量机 (support vector machine，SVM)[12]的驾驶员意图识别算法，将驾驶员意图分为直行、左转和右转3种类型。结合高精度地图提出基于最小二乘法和Bezier曲线的拟合算法，拟合出终点位置与车速/加速度的关系以及终点航向角与车速/加速度的关系，通过沿直线搜索法寻找控制点计算出多条Bezier曲线，经过代价函数筛选出1条代价最小的轨迹作为预测轨迹。在边缘计算中心平台上，验证了算法的有效性。

2 研究平台

本文的研究工作是在天津市海河教育园区中心公园环线开展的，如图1所示。该线路的17个路口进行了智慧化改造。并且采集了整个智慧道路的高精度地图，可直接获取道路限速、路网数据、车道线数据、道路边沿数据、道拓扑结构数据以及交通标志等数据。

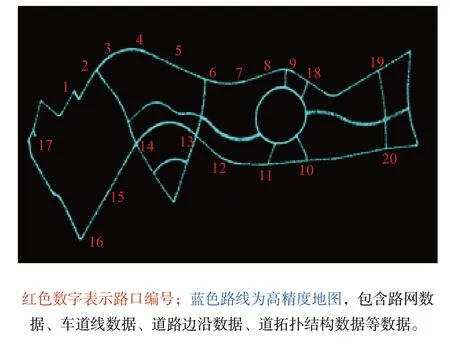
图1 智慧道路路线图

2.1 智慧道路硬件平台

在智慧道路选定的路口配置了激光雷达和Xavier等设备。Xavier是NVIDIA公司推出的一款嵌入式模块化系统，采用了ARM架构，主要为所在路口提供路侧计算服务。激光雷达是由激光器发出的脉冲激光达到目标物体，经一些散射后反射到接收器上，通过激光测距原理和激光点的数量得到目标物体距离信息和三维立体图像，主要用于交叉路口附近目标车辆的检测。

本文使用的激光雷达安装在红绿灯的竖杆上，具体感知效果如图2所示。在此平台中主要用来处理激光雷达的点云数据。设备详情如表格1所示。

图2 激光雷达感知效果图

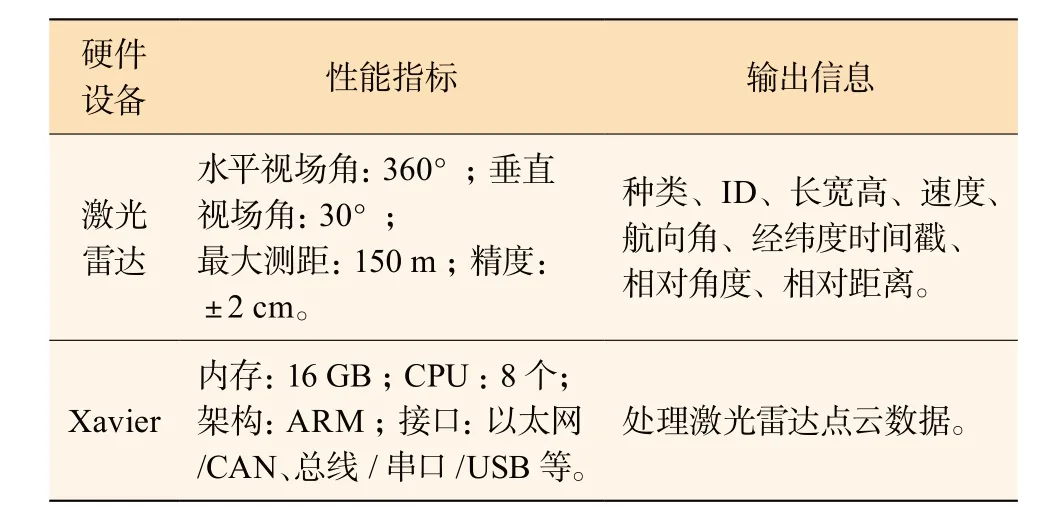
表1 传感器参数表

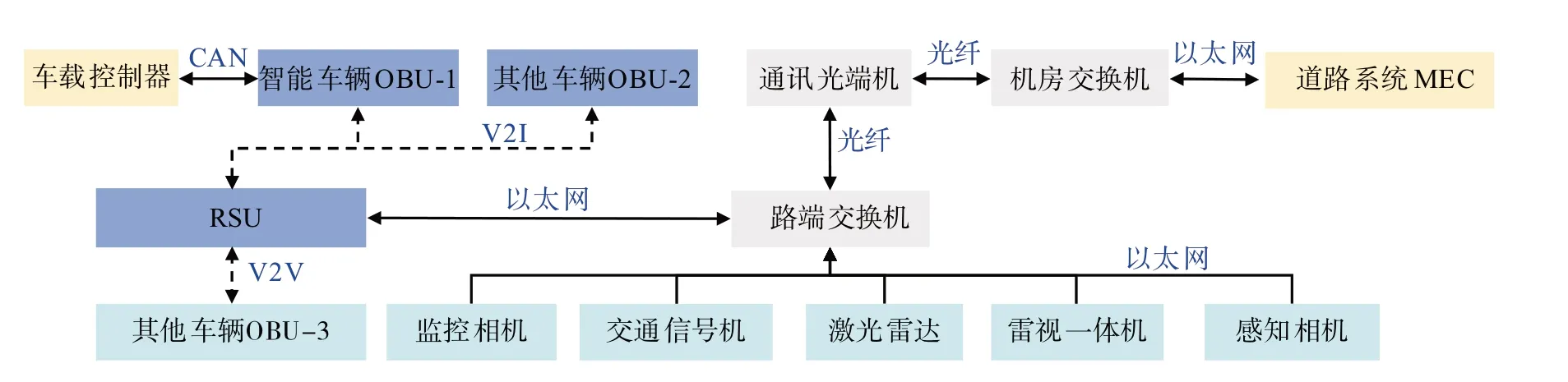
图3 路侧通讯架构图

整个智慧道路的通讯架构是由基于光纤的全道路通讯和基于V2X车联网通讯两部分组成，具体通讯架构如图3所示。沿图1所示的路线，铺设了光纤，能够保证路端所有设备的数据实时传回到边缘计算中心MEC，进行计算处理，MEC位于道路起点处天津大学新校区热动力大楼内。

2.2 交叉路口感兴趣区域

智慧道路交叉路口附近车流量很大，对路侧检测跟踪带来很大的挑战。本文预测的是即将进入路口的车辆而不是远离路口的车辆。因此本文只关心在感兴趣区域（region of interest，ROI）内的目标车辆。对图1中的9号路口进行ROI的划分，如图4所示。图4中的目标车辆位于路口前-30 m的位置，即车辆在进入路口前30 m的位置。

在图1中9号路口对230辆车进行数据采集，采集的车辆轨迹簇如图5所示。

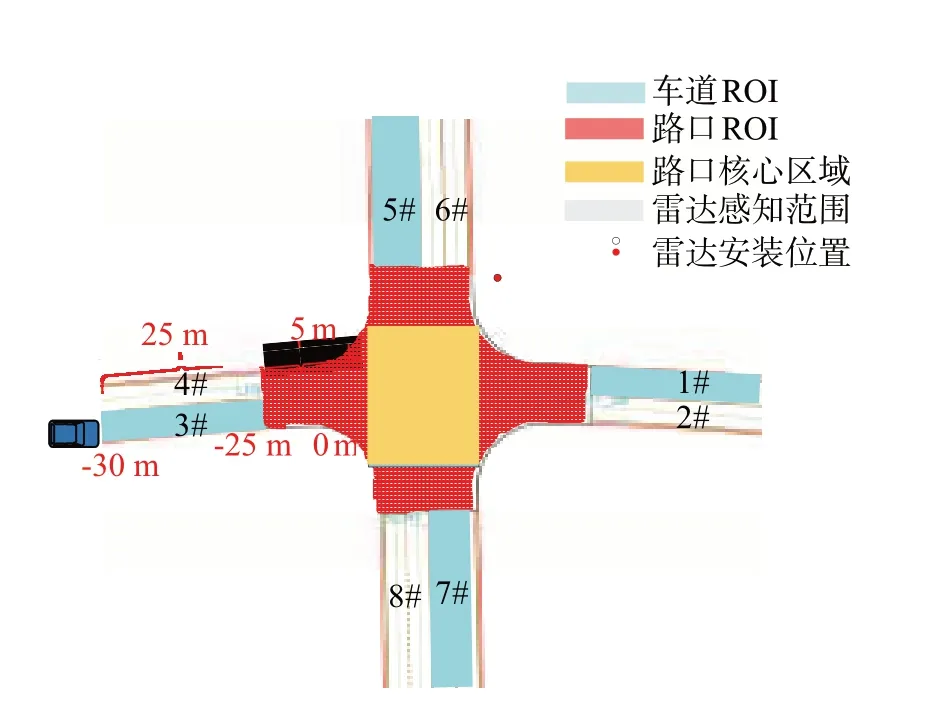
图4 交叉路口ROI图

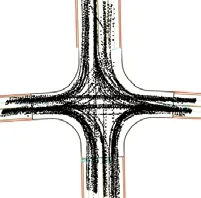
图5 路口采集车辆轨迹簇

3 交叉路口目标车辆的轨迹预测

车辆在交叉路口时可能会有3种行驶方式如直行、右转及左转，如图6所示。当车辆进入ROI时，路端激光雷达对其进行识别跟踪，输出检测的信息如位置、航向角、速度、相对角度、相对距离等。因为城市交叉路口固定拓扑结构约束和驾驶行为习惯的限制，不同驾驶意图的车辆在交叉路口时的航向角、相对角度和相对距离等信息是逐渐发生变化的。选取图6中红色轨迹簇的车辆数据进行分析。

图6 路口车辆行驶示意图

如图7所示，选取采集车辆信息的航向角θ为x轴，车辆相对距离Δd为y轴，车辆的相对角度Δα为z轴。车辆航向角指车头与正北方的夹角，往东为正。车辆的相对距离指车辆相对于激光雷达安装位置的距离。车辆的相对角度是指车辆相对于激光雷达的距离。从图中标注的位置开始，不同驾驶意图的车辆数据开始出现区别，利用这种数据的变化可对驾驶员意图进行分类。

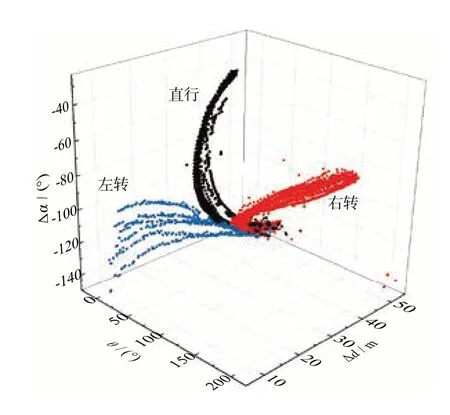
图7 路口车辆数据分布图

3.1 基于支持向量机的驾驶员意图分类算法

在交叉路口采集的数据主要用作驾驶员意图识别模型的训练数据和测试数据。本文使用SVM对交叉路口附近驾驶员意图进行分类。SVM是一种广义线性分类器，适用于小样本、非线性及高维模式中的识别[13]。当输入特征向量为高维向量时，为解决原始样本线性不可分问题，将样本x映射到高维空间，在特征空间中划分超平面对应的模型为

式中：φ(x)是将x映射后的特征向量，w和b是模型参数，满足：

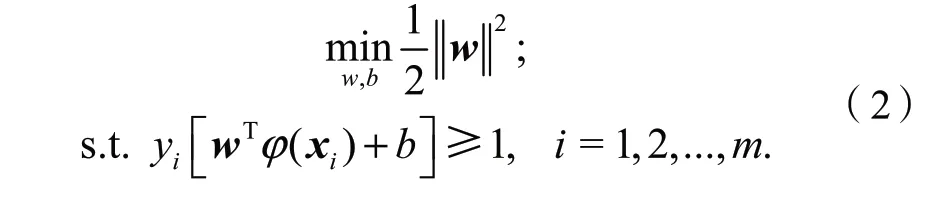
直接求解映射到特征空间后的关系式是困难的，因此可以通过求解对偶问题来简化计算，对偶表达式为

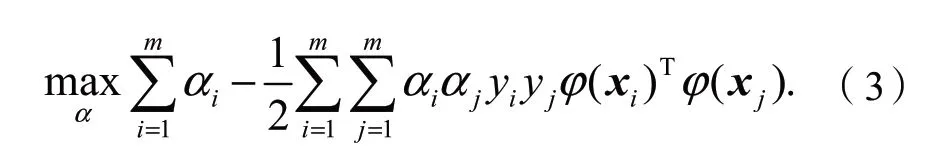
式中：α为每条约束添加的Lagrange乘子，满足C≥αi≥ 0，其中C为惩罚因子，本文设定为0.8。通过选取不同的核函数(kernel function)取代高维特征空间中的内积运算避免维度灾难。本文中选取径向基函数 (radial basis function，RBF)的Gauss核函数，其表达式为

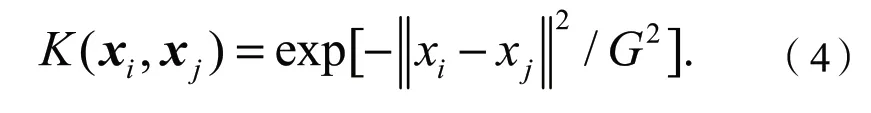
式中：G是核函数参数，本文设定为1.0。

选取与驾驶员意图相关性较强的特征向量作为模块的输入，每组特征向量给定一个标签。将标签表示为T= [-1,0,1]，其中-1表示左转，0表示直行，1表示右转。当车辆进入感兴趣区域时，根据检测的每包信息进行驾驶员意图分类并且给出相应的标签，为了防止误分类输出提高分类的准确性，加入了滑动时间窗[14]timewin= [0,0,0,0,0]，将每包数据识别出的标签逐个添加到滑动时间窗内，当滑动时间窗内出现的标签重复率达到75%以上时，输出此标签即为识别的结果。具体的模块框架如图8所示。

当车辆进入感兴趣区域(ROI)时就可获取车辆的相关信息，此时就开始预测驾驶员的意图。随着车辆到路口前距离L的变化，根据实时检测的车辆信息识别出的驾驶员意图概率P也随之发生变化。如图9所示，对于直行的车辆，车辆在进入路口前-30 m时输出的驾驶员意图为直行，当车辆在进入路口前-5 m时可输出驾驶员意图。对于左转和右转车辆，在路口前-2 m 的时候，正确的驾驶意图可进行输出。因此当车辆位置在路口前-2 m 时，输出驾驶员意图预测的最终结果。

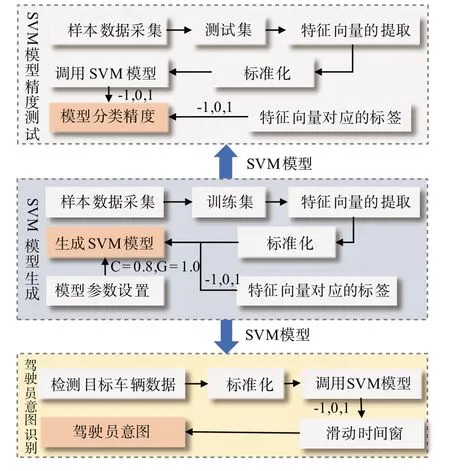
图8 驾驶员意图分类模块

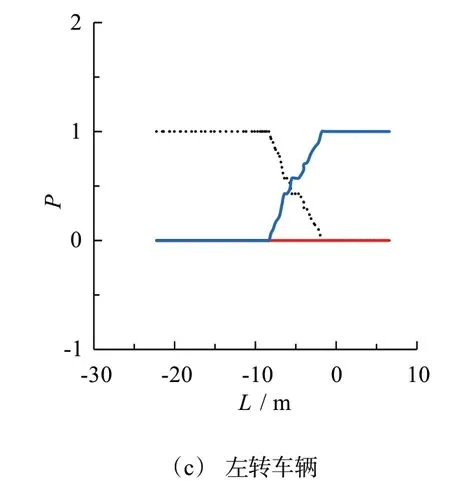
图9 驾驶员意图识别概率图

3.2 轨迹拟合

在获取驾驶员意图以后，结合高精度地图可得知目标车辆大致的行驶趋势。此时车辆的起点是已知的，终点位置也在未来某个区域内。选择Bezier曲线[15]、五次多项式[16]及B样条曲线[17]对同一车辆的轨迹进行拟合，拟合结果如图10所示。五次多项式拟合时获取车辆的起点、终点以及转弯位置，拟合结果与车辆真实轨迹偏差较大。B样条曲线拟合时需要多个控制点对曲线进行局部控制，控制点计算繁琐且拟合曲线与车辆真实轨迹匹配度较低。Bezier曲线与车辆真实轨迹匹配度最高，且所需控制点数量较少，因此选定Bezier曲线对车辆轨迹进行拟合。

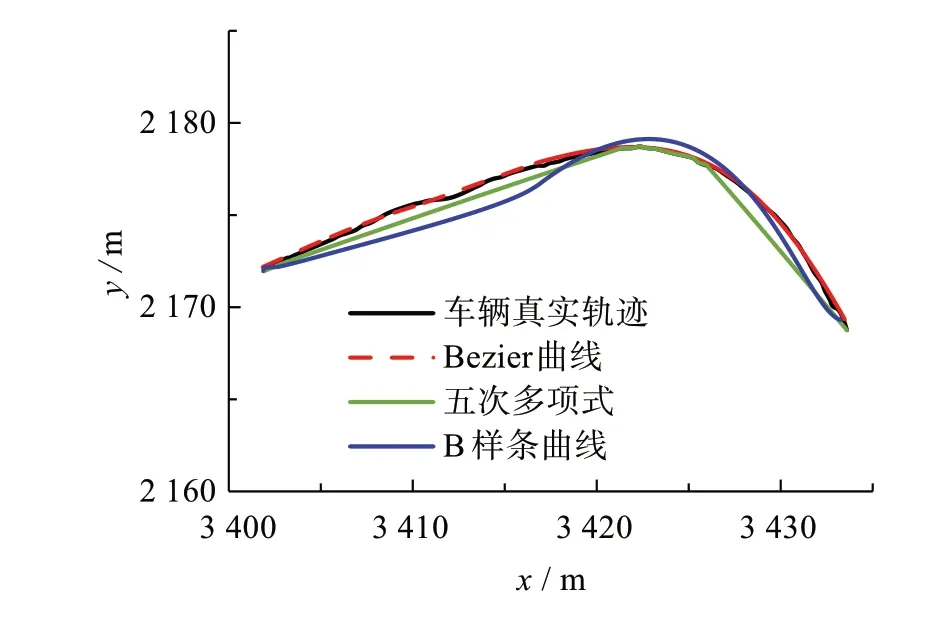
图10 拟合曲线选择

Bezier曲线是二维曲线，由起点、终点和控制点组成，通过调整控制点来调整曲线的形状。给定点P0，P1，…，Pn，则n次Bezier曲线的一般表达式为

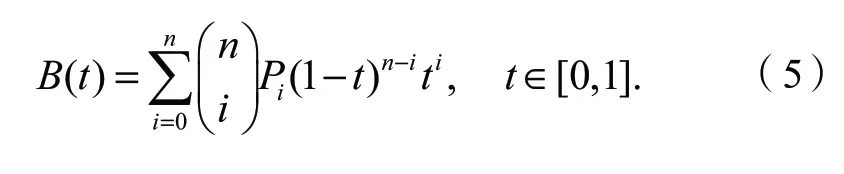
对交叉路口附近的直行车辆选取一次Bezier曲线进行轨迹拟合，P0表示起点即输出驾驶员意图时对应的坐标，P1表示终点，曲线拟合表达式为：

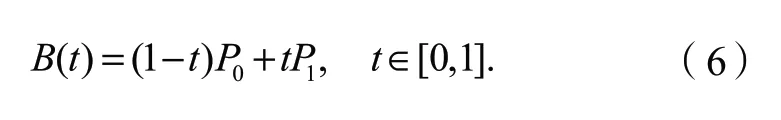
对交叉路口附近的转弯车辆选取三次Bezier曲线进行轨迹拟合，P0表示起点即输出驾驶员意图时对应的坐标，P1、P2表示控制点，P3表示终点，其表达式为

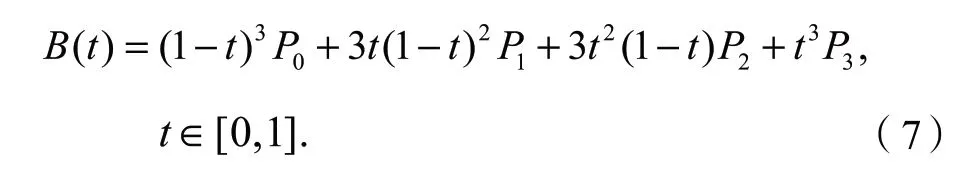
由此可知拟合曲线首先需要对终点和控制点进行计算。

3.2.1 终点计算

对于驾驶员意图为直行的目标车辆，出路口时的终点P1离车道沿边界的距离d1与输出驾驶员意图时位置P0离车道沿边界的距离d0相同，即d0=d1，如图11所示。

由图11可知：对于驾驶员意图为转弯的目标车辆，车辆初始车速v、加速度a与车辆转弯半径有关系，即转弯半径越大，终点离车道沿的距离d越大。

通过最小二乘法[18]拟合出d与v、a的关系和终点航向角θend与v、a的关系，如图12所示。

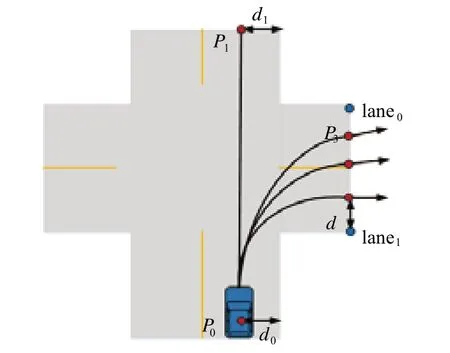
图11 目标车辆起终点示意图

若令x=v/(m·s-1)，y=a/(m·s-2)，则有：

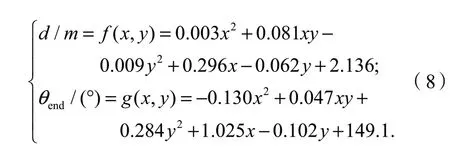
在图11中，根据高精度地图可得知交叉路口2个边界点lane0和lane1的坐标(xlane0,ylane0)、(xlane1,ylane1)，由此可求得终点P3的坐标(xP3,yP3)，即：

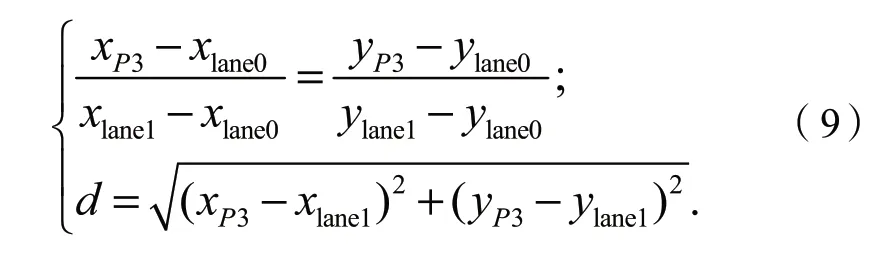
图12 距离和航向角的拟合等高图

3.2.2 控制点计算

三阶Bezier曲线需要两个控制点P1和P2来控制曲线的形状。为了求解控制点坐标，将起点P0位置沿航向角进行延长，将终点P3位置沿航向角反向进行延长，得到交点O，如图13所示。P1位于线段P0O上，P2位于线段P3O上，将2条线段N等份，然后沿直线快速搜索所有的控制点。

线段P0O的斜率k0如式(10)所示，截距b0如式(11)所示。线段P3O的斜率k1如式(12)所示，截距b1如式(13)所示，即：

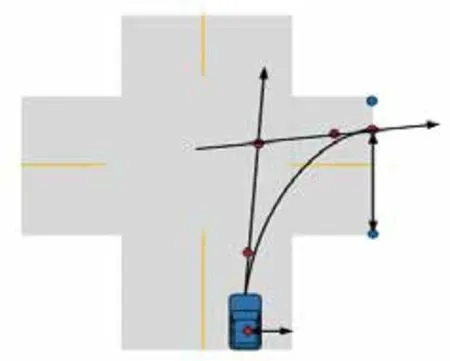
图13 目标车辆控制点示意图

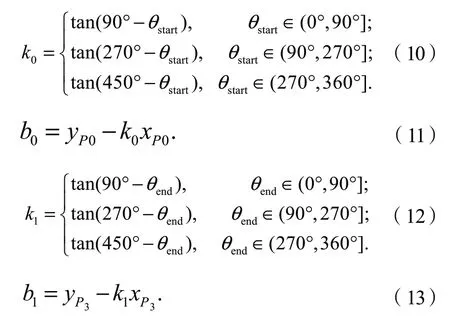
式中：θstart为车辆初始位置的航向角即输出驾驶员意图时的航向角，θend为车辆终点的航向角即式(8)中拟合出的航向角，(xP0, yP0)为车辆初始位置的坐标即输出驾驶员意图时的位置坐标，(xP3, yP3)为终点坐标即式9中求解出的终点坐标。由此，可计算交点O的坐标(xO, yO)：

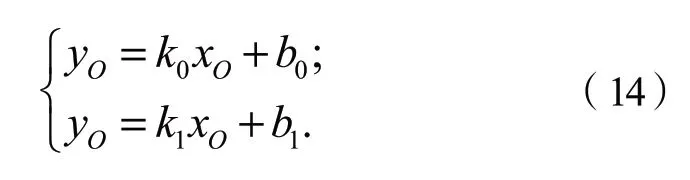
N组对应的控制点(P1,P2)的表达式如式(15)，则可以拟合出N条车辆轨迹。

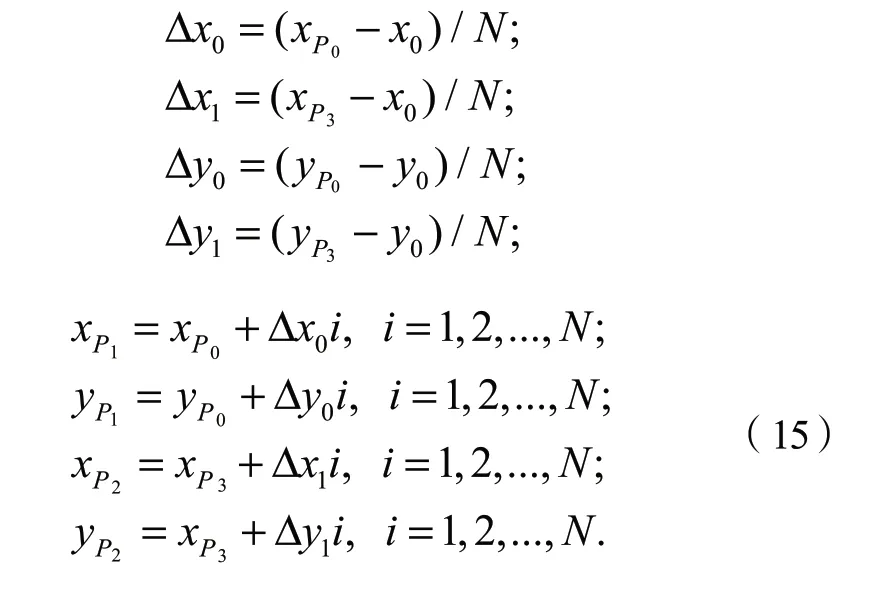
在图1中9号路口拟合的右转和左转车辆轨迹簇如图14所示。

3.3 轨迹输出

拟合出车辆的轨迹簇以后，需要选出一条可能性最大的轨迹作为车辆最终的预测轨迹，主要通过代价函数[19]来进行衡量。代价函数COST[·]由2个子代价函数构成：行驶路程代价函数与参考路径相似性函数，即：

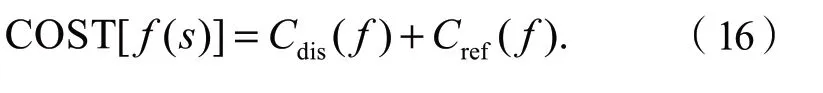
式中：f(s)为拟合的Bezier曲线方程。

行驶路程代价函数：在选取拟合轨迹时出于能耗的考虑，应考虑车辆行驶路程的大小，因此在总代价函数中加入行驶路程代价函数，即：

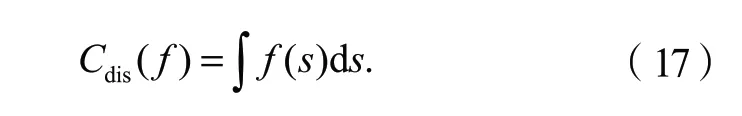
与参考路径相似性函数：主要从采集的轨迹簇里面选择一条参考路径，使用欧几里得衡量轨迹的相似程度，使车辆尽量按照参考路径行驶。欧几里得通过衡量两条曲线间的绝对距离来判断其相似性。与参考路径相似性函数为

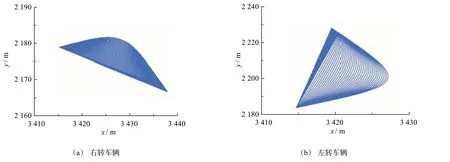
图14 9号路口拟合车辆轨迹簇

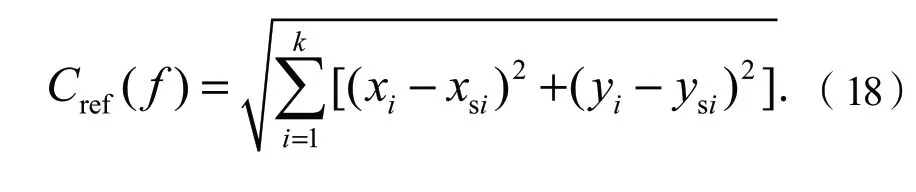
式中：(xi, yi)，（i= 1, …,n）表示拟合Bezier曲线离散化后的坐标，(xsi, ysi)，（i= 1, …,n），表示参考路径的坐标。

经过代价函数衡量后选择代价最小的一条曲线作为最终的预测轨迹进行输出。图14中拟合的右转和左转车辆轨迹簇经过代价函数后输出结果如图15所示，其中红色轨迹为最终输出轨迹。

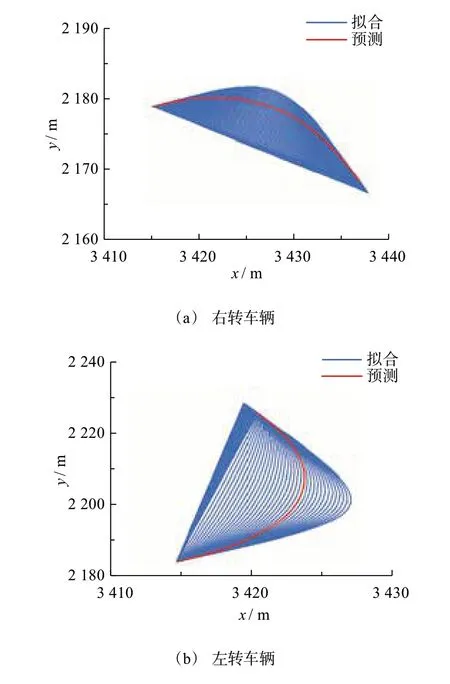
图15 9号路口预测车辆轨迹簇

4 数据分析

4.1 特征向量相关性大小分析

文中采用的激光雷达单位步长内获取的每组特征向量包括航向角θ，相对角度Δα，速度v，相对距离Δd，坐标(x, y)。为了尽可能的提高驾驶员分类的准确率，需要选取相关性更强的特征向量。因此将单个特征向量进行输入测试，训练集数量为8 870包，测试集数量为210包，其中将x坐标和y坐标一起输入。

经过试验结果如表2所示。按照单个特征向量相关性从大到小排列顺序为： (x, y)、θ、Δα、Δd、v。为了进一步提高分类模块的准确率，将单个特征向量进行择优组合输入，测试结果如表3所示。

结果表明：输入特征向量个数越多，模块分类精度越高，当输入特征向量为5个时，分类精度就可以达到92.6%可满足分类精度需求。因此选取坐标(x, y)、航向角θ、相对角度Δα以及相对距离Δd作为驾驶员意图分类模块的输入。

表2 单个特征向量测试结果

表3 组合特征向量测试结果

组合原则：

1) 选择相关性较大的单个特征向量；

2) 尽可能的保持较高的准确率。

4.2 驾驶员意图分类结果分析

在图1中的5、7、8、9号路口对120辆车进行驾驶员意图识别。表4为驾驶员意图识别结果，其中有110辆车的驾驶员意图识别结果准确，驾驶员意图识别准确率为92.5%。

表4 路口驾驶员意图识别测试结果

为了更好的保证计算的时效性，本文中驾驶员意图分类算法的训练和调用是分开进行的，程序中提前将采集的大量数据进行模型的训练工作。对驾驶员意图进行识别的时候可以直接调用模型，这样可以缩短计算的时间。图16是调用SVM的计算时间统计。主要统计：算法从接收到特征向量后识别对应的驾驶员意图标签所用的时间，平均计算时间为8.76 ms。

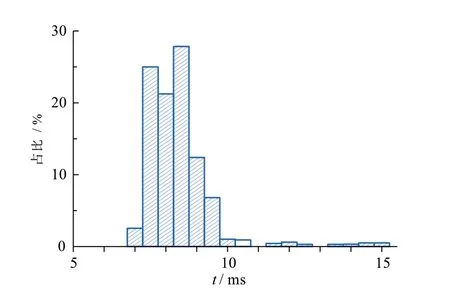
图16 调用SVM运行时间

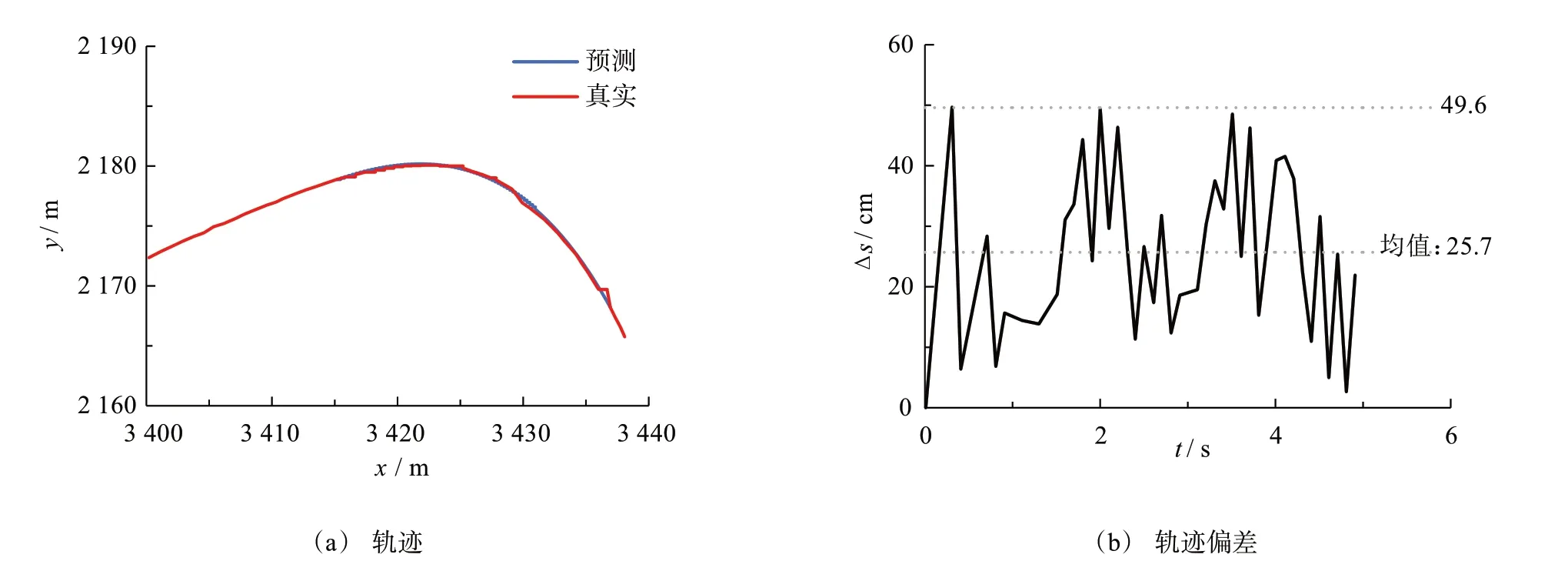
图17 预测轨迹与真实轨迹对比

图18 路口车辆真实轨迹与预测轨迹对比

4.3 轨迹预测结果分析

将图15中右转车辆输出的预测轨迹与真实轨迹进行对比结果如图17a所示，其中蓝色轨迹为预测车辆轨迹，红色为真实车辆轨迹。如图17b所示为预测轨迹与真实轨迹间的偏差，其中最大偏差为49.6 cm，平均偏差为25.7 cm，上下波动方差为0.018。

对表4中驾驶员意图识别正确的110辆车进行轨迹预测。如图18a所示，所有车辆预测轨迹与真实轨迹间的平均偏差为21.4 cm。如图18b所示，车辆预测轨迹与真实轨迹间最大偏差范围在22.3～57.9 cm之间。

5 结 论

本文提出了将支持向量机与Bezier曲线相结合的城市交叉路口车辆轨迹预测方法，并且在边缘计算中心MEC中完成所有的边缘计算过程。通过对路口车辆通行意图与轨迹特征进行分析后，将特征向量输入驾驶员意图分类模块进行分类，最后输出预测的驾驶员意图。将经Bezier曲线拟合后的多个轨迹输入到代价函数中，输出代价最小的一条轨迹作为最终预测轨迹。

经过与2个路口120辆车的真实数据对比，驾驶员意图分类准确率在92.5%以上，预测轨迹与真实轨迹间的平均偏差为21.4 cm，最大偏差范围在22.3 ～57.9 cm之间。

因此本文使用的方法能够满足城市交叉路口车辆轨迹预测的需求，为无人驾驶车辆轨迹规划提供先验信息。

参考文献 (References)

[1] 徐彪, 张放, 王建强, 等. 连续交叉路口通行辅助系统[J]. 汽车工程, 2016, 38(11): 1344-1350.

XU Biao, ZHANG Fang, Wang Jianqiang, et al. Continuous intersection traff ic assistance system [J].Automotive Engineering, 2016, 38(11): 1344-1350. (in Chinese)

[2] 邹渊, 张涛, 张旭东, 等. 考虑车流影响的网联车辆节能驾驶研究[J]. 汽车工程, 2020(10):1320- 1326.

ZOU Yuan, ZHANG Tao, ZHAGN Xudong, et al. Research on energy-saving driving of connected vehicles considering the inf luence of traff ic f low [J].Automotive Engineering, 2020(10):1320-1326. (in Chinese)

[3] XU Ting, JIANG Ruisen, WEN Changlei, et al. A hybrid model for lane change prediction with V2X-based driver assistance [J].Physica A: Statal Mech Appl, 2019, 534: 2-14.

[4] Schubert R, Richter E, Wanielik G. Comparison and evaluation of advanced motion models for vehicle tracking [C]//2008 11th Int’l Conf Info Fusion IEEE, Cologne, Germany, 2008: 1-6.

[5] Brannstrom M, Coelingh E, Sjoberg J. Model-based threat assessment for avoiding arbitrary vehicale collisions [J].IEEE Trans Intell Transp Syst, 2010, 11(3): 658-669.

[6] Houenou A, Bonnifait P, Cherfaoui V, et al. Vehicle trajectory prediction based on motion model and maneuver recognition [C]//2013 IEEE/RSJ Int’l Conf Intell Robo Syst, IEEE, Tokyo, Japan, 2013: 4363-4369.

[7] XIAO Wei, ZHANG Lijun, MENG Dejian. Vehicle trajectory prediction based on motion model and maneuver model fusion with interactive multiple models [J].SAE Int'l J Adv Current Practices in Mobility, 2020, 2: 3060-3071.

[8] FENG Xidong, CEN Zhepeng, HU Jianming, et al. Vehicle trajectory prediction using intention-based conditional variational autoencoder [C]//2019 IEEE Intell Transp Syst Conf (ITSC), IEEE, Auckland, New Zealand, 2019: 3514-3519.

[9] 张星洲, 鲁思迪, 施巍松. 边缘智能中的协同计算技术研究[J]. 人工智能, 2019(5): 55-67.

ZHANG Xingzhou, LU Sidi, SHI Weisong. Research on collaborative computing technology in edge intelligence [J].Arti Intell, 2019(5): 55-67. (in Chinese)

[10] WU Gaoxiang, MIAO Yiming, ZHANG Yu, et al. Energy eff icient for UAV-enabled mobile edge computing networks: Intelligent task prediction and off loading [J].Computer Comm, 2020, 150: 556-562.

[11] Bekkouche O, Taleb T, Bagaa M, et al. Edge cloud resource-aware f light planning for unmanned aerial vehicles [C]//2019 IEEE Wireless Comm Networking Conf (WCNC), IEEE, Marrakesh, Morocco, 2019: 1-7.

[12] Tomar R S, Verma S, Tomar G S. SVM based trajectory predictions of lane changing vehicles [C]//Int’l Conf Compu Intel Commu Networks IEEE, Gwalior, India, 2011: 716-721.

[13] 冷雨泉, 张会文, 张伟. 机器学习入门到实践[M]. 北京: 清华大学出版社, 2019: 77-86.

LENG Yuquan, ZHANG Huiwen, ZHANG Wei. Introduction to Practice of Machine Learning [M]. Beijing: Tsinghua University Press, 2019: 77-86. (in Chinese)

[14] Lam H T, Bouillet E. Flexible sliding windows for kernel regression-based bus arrival time prediction [C]//Euro Conf Mach Learning Princi Pract of Knowledge Discovery in Databases, Springer Int’l Publishing, Porto, Portugal, 2015: 68-84.

[15] ZHOU Wei, WANG Xiaoping, SUN Haoshui, et al. Trajectory optimization of quadrotor UAV based on Bessel curve [C]//2019 14th IEEE Int’l Conf Electr Meas Instru (ICEMI),IEEE, Changsha, China, 2019: 1434-1440.

[16] YUE Ming, WU Xiangmin, GUO Lie, et al. Quintic polynomial-based obstacle avoidance trajectory planning and tracking control framework for tractor-trailer system [J].Int'l J Control Automa Syst, 2019, 17(3): 2634-2646.

[17] DONG Jiajia, WANG Taiyong, ZHANG Yongbin, et al. Applications of improved B-spline curves to 6R robot trajectory optimization [J].Chin Mech Engi, 2018, 29(2): 193-200.

[18] 姚连璧, 钱瑾斐. 基于移动最小二乘法的轨迹拟合切线方位角计算[J]. 同济大学学报：自然科版, 2018, 46(11): 121- 125.

YAO Lianbi, QIAN Jinfei. Azimuth angle calculation of trajectory f itting tangent based on moving least squares method [J].J Tongji Univ：Nat Sci Ed, 2018, 46(11): 121-125. (in Chinese)

[19] Devaurs D, Siméon T, Cortés J. Optimal path planning in complex cost spaces with sampling-based algorithms [J].IEEE Trans Automation Sci Engi, 2016, 13(2): 415-424.