基于时变距离函数的多变量区间函数型主成分分析方法

孙利荣,朱丽君,徐莉妮,王凯利

(浙江工商大学 统计与数学学院,浙江杭州 310018)

§1 引言

随着现代社会数据获取和存储技术的快速发展,越来越多的复杂数据集得以涌现,其中有一类虽然是离散采集的,但是呈现出显著的连续函数特征的数据,被称之为函数型数据[1].在实际生活中,函数型数据无处不在,例如被实时高频记录的大气温度数据和股票价格数据.若需要研究的时间长度合适,与一般数据相比,函数型数据能挖掘出更多信息,给出更合理,更直观的几何解释[2].例如文献[3]对我国沪深300指数5分钟内的波动率和成交量数据进行函数型主成分分析,发现波动率呈现典型的日历效应,对数成交量呈现U型特征.若需要研究的时间长度较长,被高频记录地函数型数据的冗余信息会增多,计算复杂度会提高,使函数型数据分析的准确度下降.因此有必要在进行函数型数据分析前对数据降维处理.降维方法主要分为特征选择和特征变换两种,其中特征变换是指通过某种变换将原始的输入空间数据映射到一个新的空间中[4].符号数据分析是以符号数据代替传统的点数据来描述样本的一种特征变换方法,区间符号数据作为符号数据的一种表现形式,通过将某个时间长度内的函数型数据打包为区间符号数据,例如将某个时间长度内的股票价格数据打包为最低价格和最高价格组成的区间数据,进而形成了长度较为合适的区间函数型数据.该方法不仅使计算所需的量级极大减少,噪声影响降低,而且使提取数据长期特征的效率得到提升[5].

主成分分析是一种常见的特征提取和综合评价的方法.对于函数型数据和某个时刻的区间数据,主成分分析分别衍生出了函数型主成分分析和区间主成分分析.函数型主成分分析和区间主成分分析都是基于传统主成分分析的计算思想,在计算出数据的协方差矩阵的基础上计算出特征函数或特征向量.其中函数型主成分分析通过将离散数据拟合为函数使整个计算基于函数形式.与处理离散函数型数据的全局主成分相比,函数型主成分分析解决了时间变量的自相关性问题,放宽了约束假定,减少了计算误差,提高了可视化程度.区间主成分则主要通过改变样本的协方差计算方法来适应其区间形式,其中基于距离的区间主成分分析是其主要的研究方法.而基于距离的区间主成分分析以协方差公式为基础,认为各个样本点与均值之间偏差可以用距离来表示.区间距离的计算公式主要分为两种:(一)将经典距离公式直接引入区间偏差计算.如文献[6]定义了两个区间之间的海明距离,欧式距离,文献[7]定义了区间Hausdorff距离.(二)将区间形态引入区间偏差计算.如文献[8]认为区间的偏差应该是区间面积和区间中点的加权和,文献[9]使用Jaccard相似度计算区间偏差.对于区间函数型数据,文献[10]曾提出区间函数型主成分分析方法用于特征提取和综合评价,主要通过将区间数据序列拟合成光滑区间函数,然后将区间函数离散化成区间矩阵,通过区间主成分分析得到的特征向量进行函数拟合获得特征函数,但是该方法的本质是将指标变量转换为时间变量的区间主成分分析,无法适用于多变量的区间函数型数据.同时现有的函数型主成分分析和区间主成分分析不能直接处理区间函数型数据.基于此,研究适用于多变量的具有连续特征的区间数据的主成分分析方法,无论对丰富主成分分析方法,还是对解决现实数据的特征提取和综合评价都具有重要意义.本文将区间主成分的距离概念应用于函数型主成分分析,创新提出基于时变距离函数的区间函数型主成分分析方法,并通过我国A股市场中五支快递业股票的行情数据进行了实证分析.

§2 预备知识

2.1 函数型主成分分析

1.离散数据函数化

离散数据函数化的方法主要有插值法和平滑法两种.由于现实中的数据基本上都存在误差,所以通常使用平滑法将离散数据转化为函数.同时基函数平滑法会导致不连续点的存在,可以通过增加粗糙惩罚项来解决该问题,并能够进一步减少拟合误差.本文采用所有指标使用相同的基函数和相同的惩罚参数原则构建函数型数据,然后通过最小化具有惩罚项的误差平方和获得变量系数.下面以中点函数型数据的构建为例,具体过程如下所示.

基函数平滑法常用的基函数有傅里叶基函数和B样条基函数,前者适用于周期数据,后者适用于非周期数据,现均用φk(t)来表示第k个基函数,则样本i变量j下数据的拟合函数～xij(t)如式(1)所示.其中PENSSE为具有惩罚项的误差平方和,xij(tl)为样本i变量j在tl时刻的离散观测值,(tl)为样本i变量j的拟合函数在tl时刻的值,λ为函数型数据的惩罚参数,为样本i变量j的拟合函数的二阶导数,Φ为基函数矩阵,R为基函数二阶导数协方差矩阵,i=1,2,……,N,j=1,2,……,p,l=1,2,……,T.

根据误差平方和(SSE)和广义交叉验证值(GCV)来进一步确定基函数个数和惩罚参数,样本i,变量j的误差平方和SSEij和广义交叉验证值GCV(λ)ij的计算公式分别为式(3),式(4)所示.

其中df是自由度,df=tr(Sφ,λ)=trΦ(Φ′Φ+λR)-1Φ′.

由于本文对所有指标使用相同的基函数和相同的惩罚参数原则构建函数型数据,所以进一步使用平均误差平方和(MSSE)和平均广义交叉验证值(MGCV)来确定基函数个数和惩罚参数大小,具体如式(5),式(6)所示.

经过多次选择后,就能确认所需得基函数个数和惩罚参数,从而唯一确定拟合的形式,最后的拟合结果如式(7)所示.

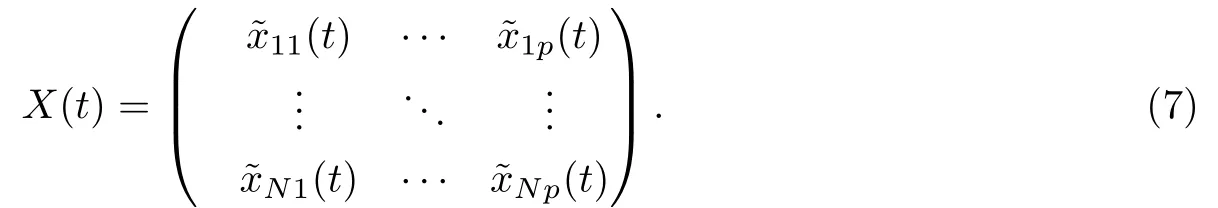
2.多变量函数型主成分分析

根据上文求得的拟合函数矩阵X(t),可以求得各个变量的均值和方差.由于本文假定所有变量均使用相同的基函数,所以均值和方差均可以用基函数形式表示,具体如式(8),式(9)所示.

多变量函数型主成分分析主要是对整体协方差函数进行特征分解,并求得相应的特征函数和主成分得分,具体步骤如下.

步骤1 计算单变量方差函数

步骤2 计算交叉协方差

步骤3 获得整体协方差矩阵

步骤4 计算特征函数和特征值

假定每一个特征函数都使用拟合函数的基函数阶数及个数,则第m个特征函数ξm(t) 的每个子特征函数为ξmh(t),h=1,2,……,p的基函数展开式为ξmh(t)=φ′(t)bmh.此时第m个特征函数ξm(t)的基函数可以表示为

其中为bmh为第m个特征函数的第h个子特征函数的基函数系数向量.

若对特征方程ξm(t)进行粗糙惩罚,则求解特征函数的公式为

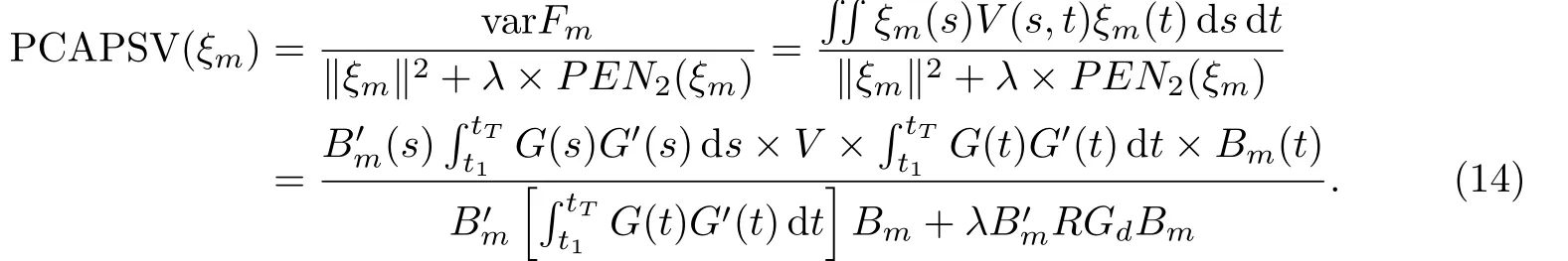
通过最大化PCAPSV(ξm),即JV J′Bm=ρm(J+λR)Bm,就可求得特征函数系数Bm及特征值ρm.具体操作为对J+λR进行对称矩阵三角分解L′L=J+λR,然后在此基础上将JV J′Bm=ρm(J+λR)Bm变换为(SJV J′S′)(LBm)=ρmLBm,最后以LBm为整体,求解得到SJV J′S′矩阵的特征向量和特征值.假定求得的特征向量为BBm,特征值为ρm,则原始特征函数基函数系数为

其中L为J+λR的上三角矩阵,S=(L-1)′.

步骤5 计算主成分得分

由步骤4结果可以获得具体的特征函数ξm(t)=G′(t)Bm(t),进一步计算第i个样本的第m个

主成分得分为

2.2 区间主成分分析

Palumbo和Lauro[7]提出基于中点-半径的区间主成分分析方法.该方法以中点代表区间位置,以半径代表区间变动,包含了更完整的区间信息.基于中点-半径的区间主成分分析思路的核心是距离与偏差的概念十分相近,因而可以采用距离来计算指标的方差和协方差.基于此,该方法定义一种区间距离来计算区间偏差,并使用计算得到的方差对中点数据矩阵和半径数据矩阵进行了标准化,然后分别求出进行中点数据矩阵和半径数据矩阵的特征向量和主成分分析,最后通过旋转半径主成分得分获得区间主成分得分,具体步骤如下.

步骤1 定义区间形式并计算区间中点和半径

其中I[x]i为第i个区间,为区间最大值,为区间最小值,为区间中点值,为区间半径值.

步骤2 定义区间距离d(I[x]i,I[x]i′)并计算单变量方差σ2

其中d(I[x]i,I[x]i′)为第i个区间和第i′个区间间的距离,σ2为单变量方差,为单变量下样本均值区间,且.

步骤3 定义总体方差-协方差矩阵

由式(21)可知,方差可以分解为中点方差,半径方差和2倍的中点和半径绝对协方差.基于上述定义,总体方差-协方差的公式为

其中Xc,Xr分别为N ×p的中点,半径数据矩阵,且均已经进行中心化处理.

步骤4 定义区间标准差矩阵

其中Σ为区间标准差对角矩阵,为区间标准差,为总体方差-协方差矩阵V中的第j个对角元素值.

步骤5 进行中点主成分分析和半径主成分分析

步骤6 计算旋转矩阵

为最大化中点数据矩阵和半径数据之间的连接,可以通过Procrustes旋转公式(26)推导出旋转矩阵A.

其中Q,P来自Xc′Xr的奇异值分解Xc′Xr=P ∧cr Q′,∧cr为Xc,Xr的奇异值矩阵.

步骤7 计算主成分得分

根据经典主成分分析的主成分得分计算方法,可以得到样本i在第k个特征向量上的中点主成分得分和半径主成分得分为式(28),(29).

其中aai为旋转矩阵A的一个向量.

§3 基于时变距离的区间函数型主成分分析

3.1 时变距离函数

函数型主成分分析的核心是通过拟合函数构建的方差和协方差函数.在基于中点-半径的区间主成分分析中,以Hausdorff距离来计算两个区间之间的偏差,该距离公式的本质是中点绝对距离和半径绝对距离之和.若直接使用函数型绝对距离式(30)来测度两个函数区间之间的偏差,则无法体现出函数型方差(协方差)的动态性.

同时,两个事物之间的差距是随时间发展而变化的,因此两个拟合函数之间的距离也应该随着时间的变化而变化.而且事物的发展会或多或少地受到其前期发展情况的影响,即在计算两个拟合函数距离时不能单纯地计算当时时间点上的距离.所以本文对式(30)进行推广,创新性地提出一种能体现变化性的区间函数距离公式―时变距离函数(Time-varying Distance Function).

函数型绝对距离的结果是两个拟合函数在t1～tT时间段内所夹的面积总和,表达的是两个拟合函数在该时间段内的累积差距.若将公式的积分上限改为变动的时间点t,则该距离表达的就是两个拟合函数在t1～t时间段内的累计差距.上述变化使公式包含了事物前期差距的影响.若直接使用该公式则会发现两个拟合函数的差距会持续拉大,这显然是不符合事实的.故对公式所计算的累积差距除以时间段t～t1,通过平均化累积差距体现较为符合实际差距波动,最终公式如式(31)所示.

3.2 区间时变距离函数计算

以中点函数型数据的时变距离函数计算为例,首先拟合中点函数型数据,获得中点均值函数,然后计算中点函数及其均值函数之间的时点绝对距离,方法见式(32),(33).然后使用基函数平滑法和粗糙惩罚项对时点绝对距离数据进行函数拟合,结果见式(34).

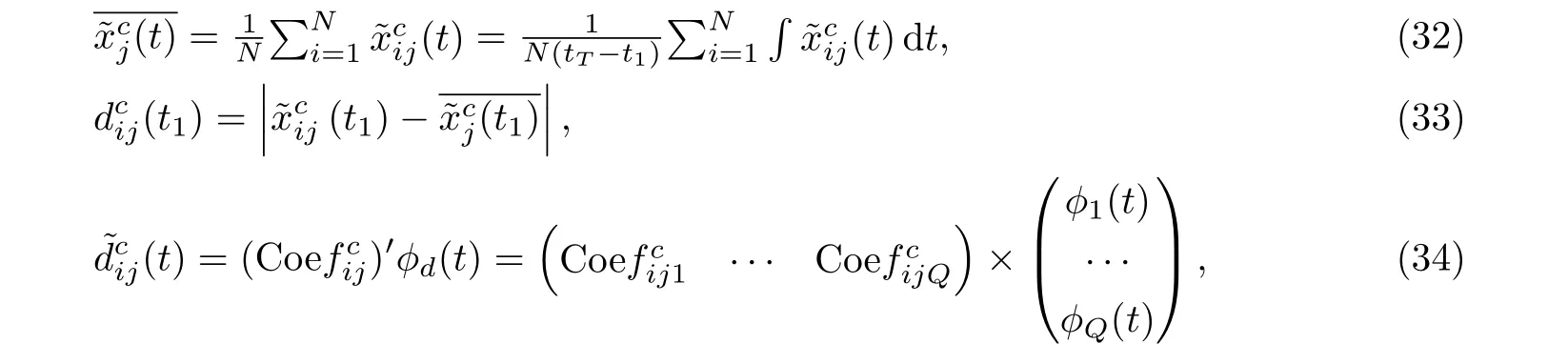
在获得时点绝对距离的拟合函数后,即可通过积分计算获得时变距离函数,具体见式(35).

在获得中点时变距离函数和半径时变距离函数后,可以获得第j个变量的区间时变距离函数t如式(36)所示.

3.3 基于时变距离函数的多变量区间函数型主成分分析

在获得区间函数型数据的区间时变距离函数后,根据基于中点-半径的区间主成分分析距离可以近似替代偏差的思想,将函数型主成分分析的单变量方差函数中偏差函数更改为区间时变距离函数,即可推导出区间方差函数,如式(37)所示.

由于函数型数据具有自协方差,所以最终的方差为式(38).

在原有交叉协方差函数的基础上,将原有函数与其均值之间偏差改为区间时变距离函数,从而推导出两个不同变量间区间交叉协方差函数公式,如式(39)所示.

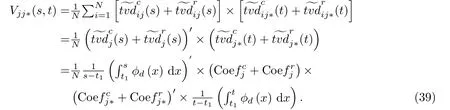
参考Ramsay和Silverman[11]的多变量函数型数据的协方差函数矩阵写法,结合已计算出来的区间方差函数和区间交叉协方差函数,区间函数型数据的总体协方差矩阵写法如式(40)所示.

假定每一个特征函数都使用时变距离函数的基函数阶数及个数,则第m个特征函数ξm(t)的每个子特征函数为ξmh(t),h=1,2,……,p,基函数展开式为.此时第m个特征函数ξm(t) 的基函数可以表示为公式(41).

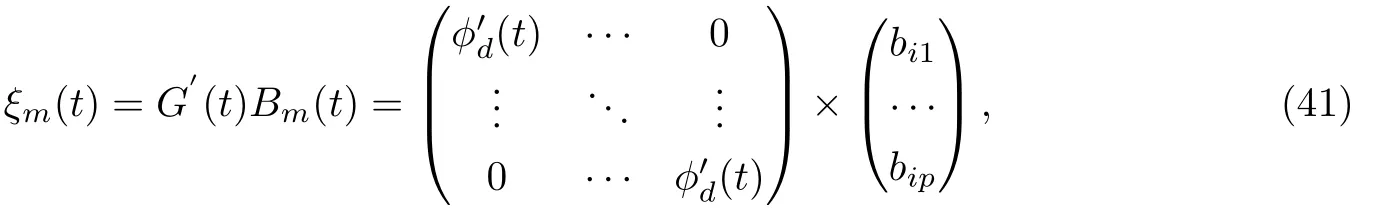
其中bmh为第m个特征函数的第h个子特征函数的基函数系数.

若对特征方程ξm(t)进行粗糙惩罚,则求解特征函数的公式为

其中L为W+λRGd的上三角矩阵,S=(L-1)′.

获得特征函数ξm(t)=G′(t)Bm(t) 后,即可计算第i个样本的第m个主成分得分为

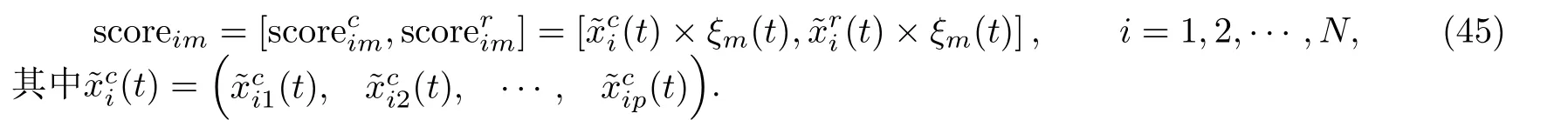
§4 实证分析

4.1 数据预处理与数据展示

本文收集了中国证券监督管理委员会《上市公司行业分类指引》(2012年修订)中邮政业的5支股票(圆通速递,韵达股份,顺丰控股,申通快递和德邦股份)2019 年1月28 日至2020年1月10 日的每日市盈率,换手率,收益率,风险因子和振幅数据(数据来源于国泰安CSMAR 经济金融数据库和同花顺ifind金融数据库),并将其按周进行区间符号数据分析,形成了最小值和最大值组成的离散区间函数型数据.在距离计算中(假定均匀分布),最小值和最大值区间与中点值和半径值区间所包含的信息量一致.因此进一步地,本文将最小值和最大值组成的离散区间函数型数据按照式(18),(19)处理成中点值和半径值组成的离散区间函数型数据.

对5支邮政业股票的每周市盈率,换手率,收益率,风险因子和振幅离散区间函数型数据进行多变量区间函数型主成分分析.采用离散数据函数化中的方法,使用4阶B样条基函数对48期离散区间函数型数据进行拟合.在基函数阶数为4阶时,误差平方和随着惩罚参数的增大而增大,广义交叉验证值随着惩罚参数的增大而减小,如图1所示.拟合后的5支邮政业股票的每周收益率中点函数和半径函数如图2所示.

图1 4阶基函数下的误差平方和和广义交叉验证值

由图2可知,从周平均收益率(中点曲线)来看,5支邮政业股票之间的收益率差别不大,其中德邦股票和申通快递的周平均收益率变动较大,收益较不稳定.5支邮政业在第25周(2019年8月)附近出现共同的收益率低点,可能是因为8月快递业务量增速放缓,整体经济压力较大.从周收益率波动情况(半径曲线)来看,5支邮政业股票的周收益率波动整体上呈下降趋势,其中申通快递一直保持高波动变动.同时半价曲线在第4 周附近出现了共同的波动高点,这说明收益率在3月份附近出现极端值,由于周平均收益率在此时变动较小,说明这有可能是由于3月份整体快递业务收入增加,带动快递业股票整体价格上升,市场部分看好,但市场也有对未来快递业发展的消极意见,因而拉大了收益率波动幅度.

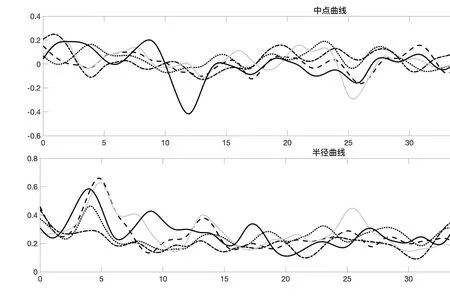
图2 5只邮政业股票的每周收益率的中点函数和半径函数

4.2 邮政业股票综合评价

在获得中点和半径绝对函数后,通过协方差计算中的方法,即可求得多变量协方差矩阵函数.进一步地,使用基于时变距离函数的多变量区间函数主成分分析方法对在2019年1月28日至2020年1月10日间邮政业5支股票的进行动态综合评价.

由图3可知,第一主成分的贡献率为87.84%,能够充分反映原有数据的信息.同时,第一主成分对中点和半径均值函数都施加了一个显著的正向影响.进一步观察第一主成分每个变量下的特征函数(图4)发现,虽然第一主成分中的各个变量在不同时间点有不同的权重,但是总体而言,各个变量的权重均为正值且相差不大,因此将第一主成分定义为各行业在股票市场表现的综合水平.

图3 中点,半径第一主成分偏离均值函数图

虽然第一主成分表示综合水平,但是每个特征函数在不同时期有不同的特征函数值,说明不同变量特征函数在总体下有自己独特的变化.市盈率代表投资于某一种股票收回投资成本所需要的年数[12],代表股票的投资价值.由图4可知,市盈率的特征函数从2019年8月开始的特征函数值显著高于其他时期,说明这期间的市盈率会显著影响股票的整体市盈率.市盈率变量特征函数值的变动与我国快递业的业务量和业务收入有一定的关系,在增速快的时期,特征函数值较大.换手率是股票转手买卖的频率,反映了股票交易的活跃程度,换手率越高说明投资者购买该支股票的意愿越强烈,该股的交易程度也就越活跃.由换手率的特征函数可知,特征函数值在第5周(2019年3月中上旬)和26周(2019年8月中上旬)附近出现高峰,说明这两个时间段对邮政业股票交易的活跃程度产生了显著影响.这主要是因为2019 年3月和2019年8月的快递业务量或快递收入的较它们前一个月有显著提升,从而引发市场看好,股票交易活跃.收益率是反映股票收益水平的指标.收益率的特征函数虽然整体波动变化较大,但其中蕴含着一定规律.将x坐标轴按月份进行划分,可以发现在大部分月份内,特征函数赋予月初的权重较高,月末的权重较小.这说明月初的收益率对股票的收益率影响较大,月末的收益率对股票的收益率较小,这也与现实股票市场中存在的收益率月初效应和月末效应相吻合.风险因子,即贝塔系数,用于衡量个别股票相对于整个股市的价格波动情况.由风险因子的特征函数可知,它在第四季度的权重值较高.将第四季度的风险因子与市盈率相对比,两者变化较为相似,即高市盈率与高风险可能存在一定的影响关系.振幅是股票的当日最高价和最低价之间的差的绝对值与昨日收盘价的百分比,它在一定程度上表现股票的活跃程度.振幅虽然是反映股票活跃程度的指标,但是其计算方法与股票价格相关,所以其特征函数变动趋势与收益率较为相似.在振幅变动较大,股票交易活跃的时候,股票的收益率一般较高.

图4 多变量区间函数型主成分分析第一主成分特征函数

根据第一主成分得分对5支快递业股票进行评价,发现在被评价时间内,中心得分排名为:申通快递＞德邦股份＞圆通速递＞韵达股份＞顺丰控股.根据5支快递业股票2019 年半年度报告,申通快递上半年业务量为30.12亿件,同比增长47.25%,业务量增速高于其他快递业股票.同时2019年3月26日申通快递与浙江菜鸟供应链管理有限公司签署《业务合作协议》,在多方面展开深度合作,进一步提升了申通快递的快递揽收派送数量及品牌影响力,从而提高了申通快递股票得分.韵达股份,德邦股份和圆通速递业务量的同比增速分别为44.71%,35.79% 和35.15%,业务量的快速增加导致外界对这几支股票普遍看好.由于顺丰控股2019 年上半年的业务量同比增长8.56%,增速显著放缓,使得股票中心得分最低.同时顺丰进行多元化布局,在同城,快运,冷链等方面均有发展,使顺丰股票的变动更加平稳.

表1 第一主成分得分值

§5 结论与展望

本文针对现实中出现的区间函数型数据问题,提出了基于时变距离函数的区间函数型主成分分析方法.以圆通速递,韵达股份,顺丰控股,申通快递,德邦股份5支邮政业股票为研究对象,对市盈率,换手率,收益率,风险因子和振幅5个变量进行区间函数型拟合,并应用区间函数型主成分分析对股票进行综合评价.基于时变距离函数的多变量区间函数型主成分分析结果显示,第一主成分贡献率为87.84%,其特征函数值均为正值,且相差不大,可以用于评价各支股票的综合水平.同时基于时变距离函数的多变量区间函数型主成分分析同时融合中点和半径数据,提取的信息量更为充分.因此在综合评价中,基于时变距离函数的多变量区间函数型主成分分析是相对较优的模型.

本文提出的基于时变距离函数的区间函数型主成分分析本质上假定了区间服从均匀分布,为充分利用区间信息.在现实生活区间数据可能是服从其他的概率分布,如正态分布,泊松分布,因此基于概率分布的区间函数型主成分分析也是一个值得研究的方向.同时在基于时变距离函数的区间函数型主成分分析与其他方法进行对比研究时,没有已有文献提供方法的效度对比指标,只能从实际案例出发说明模型的优劣性.因此,关于函数型主成分分析或者区间函数型主成分分析模型的效度指标研究也是一个值得研究的方向.