多孔介质中的Brinkman-Forchheimer模型的解的连续依赖性

石金诚,李远飞

(广州华商学院,数据科学学院,广东广州 511300)

§1 引言

近年来,许多学者对偏微分方程解的连续依赖性问题进行了广泛的研究.这意味着人们越来越重视这种由模型本身系数的变化而引起解的变化,这就是偏微分方程的结构稳定性研究.通过这种结构稳定性的研究,可以帮助了解模型在物理中的适用性.这种结构稳定性的研究是非常有必要的,因为在实际的建模过程中,数据的测量和计算都会不可避免的产生误差,必须知道一个微小的误差能否引起解的急剧变化.[1]

多孔介质在生活中是广泛存在的,多孔介质中流体方程组的解的性态研究已经成为数学与力学领域的热点问题.目前已有的研究主要是集中在Brinkman,Darcy和Forchheimer方程组的模型上.在Nield和Beijan[2]与Straughan[3]的书中广泛地讨论了多孔介质中的这些模型.参考文献中有一些论文讨论了Brinkman,Darcy,Forchheimer和其他多孔介质方程的Saint-Venant原则,但主要是研究多孔介质中的流体方程组的空间衰减估计结果(见[4]).关于多孔介质中的流体方程组的结构稳定性的研究已经由Franchi 和Straughan[5],Payne和Straughan[6],Lin和Payne[7]等人进行.近年来,文献[8-21]取得了一些新的结果.当流速过大时,Darcy定律不成立时,此时Brinkman模型被认为是准确的,此时如果用Forchheimer的逼近,就能得到如下Brinkman-Forchheimer方程组[3]:

其中ui,p,T,C分别表示为速度,压强,温度和盐浓度.gi(x)和hi(x)为重力函数,Δ为拉普拉斯算子.σ是Soret系数,此外v和b分别是Brinkman系数和Forchheimer系数.在方程组(1)中v,b,σ,k1,k2都是大于零的常数.一般来说,热扩散系数k1和盐扩散系数k2相差很大,这就产生了有趣的效果,因此,假设k1/=k2.

方程组(1)在Ω×[0,τ]区域内成立,其中Ω是R3中的一个有界单连通的星形区域,τ是给定的常数且0≤τ ＜∞.边界条件为

此外,初值条件为

本文主要研究方程组(1)的解对Brinkman系数v的连续依赖性.相比已有文献,由于盐浓度C的方程中含有σΔT项,导致以往的方法得不到盐浓度C的最大值以及一些其他的估计.本文通过引入一个新变换,得到了较好的结果.

文中采取以下符号约定,用逗号表示求偏导,用,i表示对xi求偏导,如:u,i表示为,重复指标表示求和,表示Lp范数.

§2 温度T和盐浓度C的先验界

本节将会得到一些温度T和盐浓度C的先验估计.

引理2.1温度T和盐浓度C满足以下最大值估计.

证在[22]中，Payne,Rodrigues和Straughan得出了下面的结果

接下来,需要得到C的一个界.现在定义一个新函数

则方程(1)4可以变形为

由(7)式可知

则方程组(1)可重新写为

函数N满足的边界条件为

满足的初值条件为

由于N满足与T相同的方程,所以有

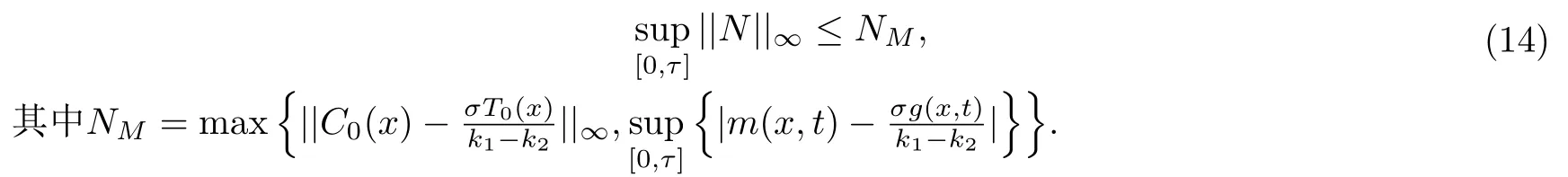
因此,C满足下面的最大值估计

引理2.2温度T和盐浓度C的范数满足以下估计.

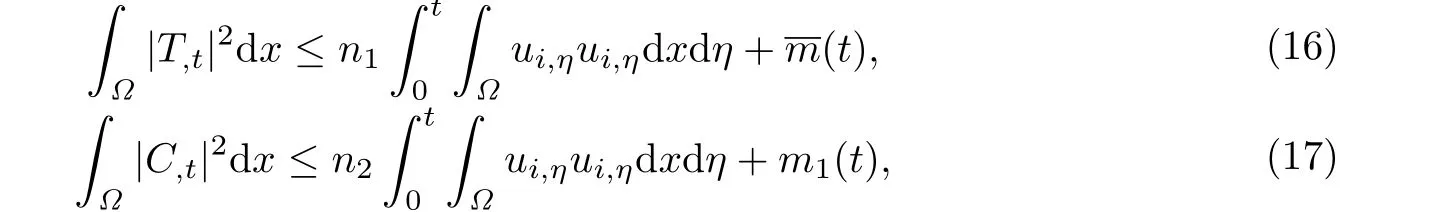
其中n1,n2均是大于零的常数,(t),m1(t)均是大于零的函数.

证文献[16]中(3.47)式在本文中依然有效,取ε6=2,可得

按照同样的步骤,也可以得到

根据N(x,t)的定义,可得

将(18)式和(19)式代入(20)式,可得

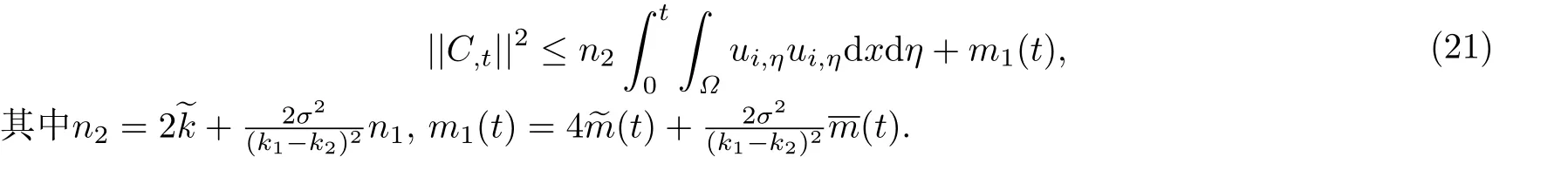
§3 Brinkman系数v的连续依赖性结果

本节建立解对Brinkman系数v的连续依赖关系.设(ui,p,T,C)为下列边界初值问题的解

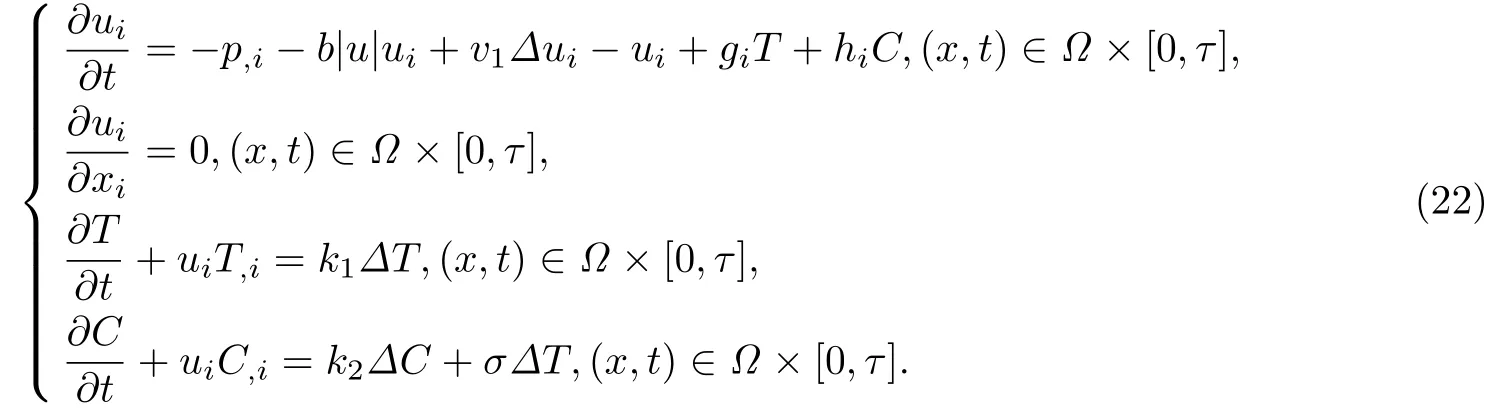
其中边界条件与初值条件为

其中边界条件与初值条件为

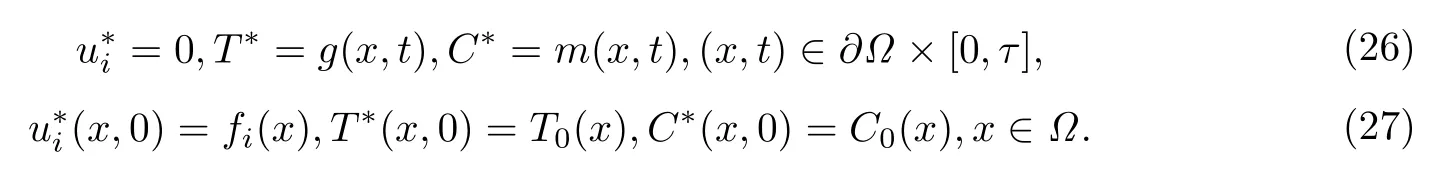
假设ωi=ui-,θ=T -T*,S=C-C*,π=p-p*,则(ωi,θ,S,π)满足下列方程组

边界条件为

此外,初值条件为

引理3.1对于速度ui,有以下估计.

其中K1(t)是大于零的函数.

证由方程(22)1,可得

联合(32)式,(16)式和(17)式,可得

则(33)式可写为

由(34)式可知

其中α=+1+g2+h2.对(35)式两边同时在[0,t]上积分,可得

假设p(x,0)=q(x),由方程(1)1,可得

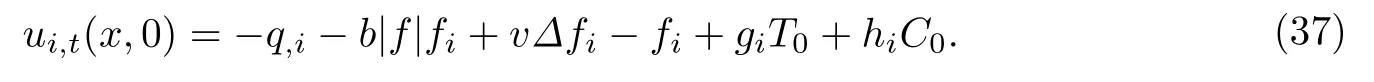
因此有

引理3.2对于速度ui,有以下估计：

其中K2(t)是大于零的函数.

证有下面的式子成立.

在方程(22)1两边同时乘以ui,并且在Ω上积分,可得

其中|Ω|为Ω的体积.

接下来将给出||∇u||2的界.在方程(22)1两边同时乘以ui,并且在Ω上积分,可得

联合(42)式和(38)式,可得

主要结果如下.

定理1设(ui,T,C,p)为初边值问题(22)式-(24)式的经典解,为初边值问题(25)式-(27)式的经典解,(ωi,θ,S,π)是这两个解的差.当Brinkman系数v1趋于v2时,解(ui,T,C,p)收敛于解.解的差(ωi,θ,S,π)满足

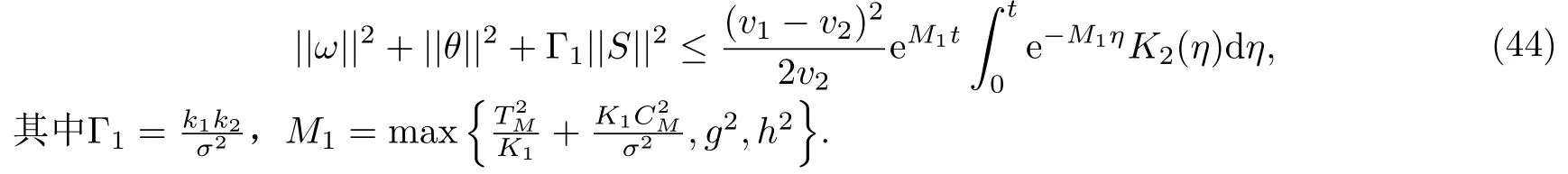
证将方程(28)1乘以ωi,并在Ω上积分,同时利用(40)式,可得

将方程(28)3乘以θ,并在Ω上积分,可得

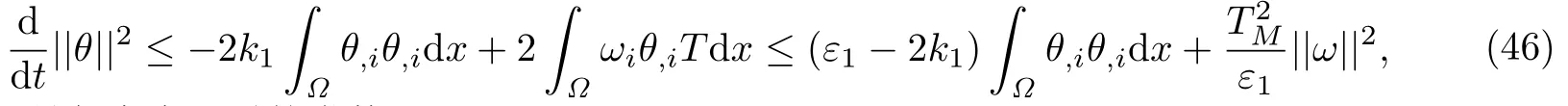
其中ε1是任意大于零的常数.

将方程(28)4乘以S,并在Ω上积分,可得

不等式(49)表明了在指定测度下当Brinkman系数v1趋于v2时,ui收敛到,T收敛到T*,C收敛到C*.

§4 结论

本文研究了在R3中有界区域上Brinkman-Forchheimer方程组的解对Brinkman系数v的连续依赖性,采用文中的方法,同样可以得到解对其他系数连续依赖性结果.后续将尝试研究在无界区域上的Brinkman-Forchheimer方程组的结构稳定性,由于此时盐浓度和温度的估计很难得到,故需要全新的方法来解决这个问题,因此研究方程组在无界区域的结构稳定性是有意义的.