Burgers-Fisher方程改进的交替分段Crank-Nicolson并行差分方法

潘悦悦,吴立飞,杨晓忠

(1.华北电力大学 控制与计算机工程学院,北京 102206;2.华北电力大学 数理学院,北京 102206)

§1 引言

本文研究数学物理中一类重要的偏微分方程,Burgers-Fisher(B-F)方程[1-2]:

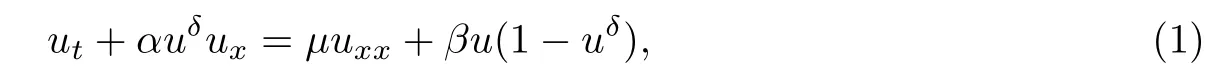
B-F方程是刻画扩散传播,对流传导作用的典型模型,可以大量用于气体动力学和热传导的研究[3].其中,α ＞0,μ ＞0,β ＜0为常数.当β=0时,方程(1)为经典的Burgers方程;当α=0时,方程(1)为一维Fisher方程.

在Burgers-Fisher方程(1)的实际计算中,通常取有限的计算区间(a,b).本文考虑Burgers-Fisher方程(1)的如下初边值问题,

初始条件:

边界条件:

分别取确定的f(x),g1(t)和g2(t),

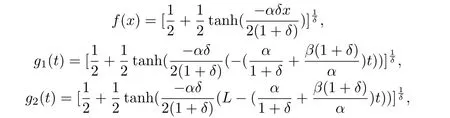
可得到解析解为

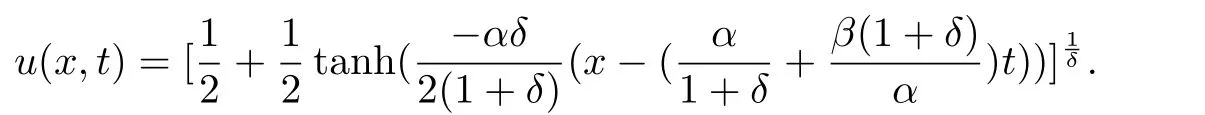
对于Burgers方程的数值研究,已有大量研究成果[4-8].但关于Burgers-Fisher方程的并行数值方法研究尚不多见.Kaya和El-Sayed(2004年)[9]研究了广义Burgers-Fisher方程的分解格式,在不使用任何离散技术的情况下,得到数值解,并与精确解比较,证明该方法具有较高精度.Zhang等(2014年)[10]利用孤立波解提出了Burgers-Fisher方程的一个新精确差分格式和非标准有限差分格式,并证明了其精度.Namjoo等(2018年)[11]考虑了广义Burgers-Fisher方程的非标准有限差分格式,讨论了其正定性,一致性和有界性.然而,文献中的大部分格式只考虑了计算精度,忽略了格式的计算效率.

随着大型并行计算机的迅速发展,研究和构造适用于大型并行计算机的计算方法成为主流.大规模并行计算的瓶颈之一是全局通讯耗时多,同步等待时间长.为了保证计算过程无需进行全局通讯,人们开始研究能适应大型并行计算机的并行数值解法.Zhang和Li(1994年)[12]将具有理想并行性的显格式和稳定性好的隐格式,Crank-Nicolson格式结合,建立了兼具稳定性和并行性的交替分段Crank-Nicolson格式.周毓麟(1997年)[13]建立了具有并行本性的差分方法的基本理论,针对拟线性抛物型方程组,构造了非均匀网格上的具有并行本性的差分格式,证明了差分解的先验估计,从而得到离散解的存在性,唯一性,收敛性和稳定性.受到构造并行本性差分方法的启示,目前,许多发展方程都可以用此并行差分方法进行数值求解,并且可以直接和有效地在并行机上应用[14-15].Sheng等(2007年)[16]提出两个并行本性差分格式,通过使用前两个时间层在边界点的值,得到内边界条件,用全隐式计算子域中的值,然后更新边界值,得到全局并行算法.曲富丽和王文洽(2007年)[17]设计了KdV方程的交替分段显-隐差分格式,理论分析格式的线性绝对稳定性,并通过数值试验验证了格式具有较高的计算精度.Guo和Liu(2013年)[18]构造了四阶抛物方程的一般交替差分格式,数值试验以交替分组显式,交替分段显-隐式和交替分段Crank-Nicolson格式为例,验证了格式的收敛性,稳定性和计算精度.Xue和Feng(2018年)[19]提出了对流占优扩散方程的一种新并行差分方法,在相同时间层使用两种区域分解法,并取平均值得到新的数值解,数值算例证明算法具有较高的计算精度且适用于并行计算.Pan等(2020年)[20]构造了Burgers-Fisher方程的交替分段纯显-隐和交替分段纯隐-显格式,数值试验证明PASE-I(PASI-E)差分格式具有空间和时间二阶精度,获得了稳定性和并行性兼顾的结果.并行本性差分格式可以直接应用到分布式内存的并行计算机系统,使得处理机之间的通信量极小,容易平衡计算和通信,从而得到好的精度和并行计算的可扩展性.本文将以这类传统并行差分格式为基础,构造改进的交替分段Crank-Nicolson差分方法求解Burgers-Fisher方程.

本文结构安排如下:§2将Crank-Nicolson格式做分段化处理,分段点处交替使用显格式和隐格式,得到改进的交替分段Crank-Nicolson(IASC-N)格式.§3给出Burgers-Fisher方程IASC-N并行差分格式的理论分析.§4的数值试验结果验证理论分析的正确性和IASC-N格式计算效率的优越性.

§2 IASC-N并行差分格式

对求解区域[0,L]×[0,T]进行网格剖分,取空间步长和时间步长,其中M,N是正整数.记xi=ih(i=0,1,2……·M),tn=nτ(n=0,1,2……·),用表示解析解U(xi,tn)的数值解.为了构造方程(1)的IASC-N格式,先分别给出以下三种离散格式.

(1) 古典显式格式

(2) 古典隐式格式

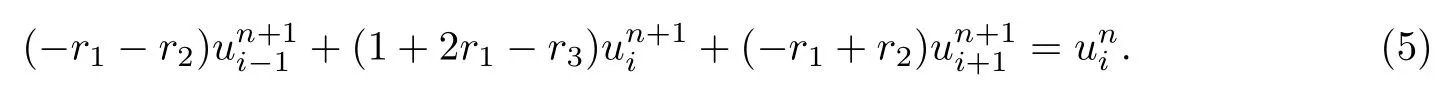
(3) Crank-Nicolson格式

现在讨论Burgers-Fisher方程的交替分段并行差分格式,本文的IASC-N格式将结合以上几种差分格式使用.

设M -1=Jl,(J ≥3,l ≥3为正整数,且J为奇数),将同一时间层上计算的点分为J段,记为S1,S2,……,SJ.以M=26,J=5,l=5为例,定义每段的内边界点及内点,构造IASC-N格式.

S1段有一个内边界点=6及4个内点i1=2,3,4,5;S2段有两个内边界点=7,=11及3个内点i2=8,9,10;S3段有两个内边界点=12,=16及3个内点i3=13,14,15;S4段有两个内边界点=17,=21及3个内点i4=18,19,20;S5段有一个内边界点=22及4个内点i5=23,24,25,26.

设n为偶数,在第n层上的数值解为已知,现计算.n+1时间层上,在点xi(i=处使用古典显式格式(4),在点处使用古典隐式格式(5),其余各点处使用经典C-N格式(6).n+2时间层上,将n+1时间层显式格式(4)的位置变为隐式格式(5),隐式格式(5)的位置变为显式格式(4),其余各点仍使用经典C-N格式(6).交替使用n+1层和n+2层上的格式,可得到IASC-N格式.具体参见图1,□采用(4)式,■采用(5)式,*采用(6)式,其矩阵形式为

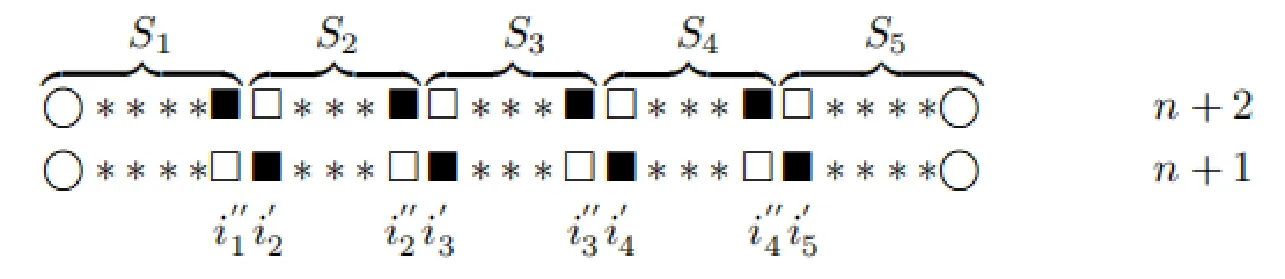
图1 IASC-N格式构造示意图

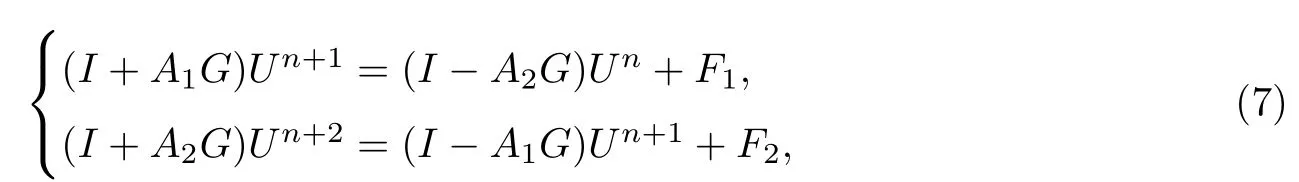
式中

Un,F1,F2都是(M -1)维向量,A=-r1-r2,B=-r1+r2,I是(M -1)阶单位矩阵.A1和A2均是(M -1)阶对角矩阵,且满足A1+A2=I.A1=diag(θ1,θ2,……,θM-2,θM-1),其中

§3 IASC-N并行差分方法的数值分析

3.1 IASC-N差分格式解的存在唯一性

为讨论IASC-N格式解的存在唯一性,需要引入如下两个引理.

引理1(Kellogg引理[21]) 设θ ＞0,矩阵(G+GT)是非负定的,则(θI+G)-1存在,并且有

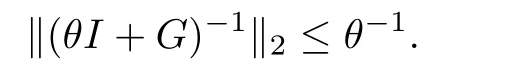
引理2由IASC-N格式(7)定义的矩阵A1G和A2G是非负定矩阵.

证明引理2,只需证明A1G+(A1G)T和A2G+(A2G)T是非负定矩阵.作如下计算

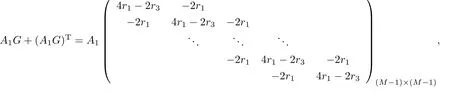
考虑低速流情况,不妨设0＜u ＜1.由于β ＜0,r3＜0,则A1G+(A1G)T是对角占优的三对角矩阵,其主对角元素为正实数.显然A1G+(A1G)T是非负定矩阵,同理A2G+(A2G)T也是非负定矩阵,故A1G和A2G是非负定矩阵.引理2证毕.

由Burgers-Fisher方程的初边值条件可知,U0的值已知.假设第2n层已经确定,求解第2n+1层差分方法的矩阵方程为

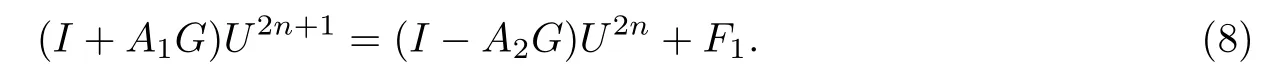
由引理1和引理2,等式右侧已知,且(I+A1G)-1存在,所以方程(8)有唯一解.

同样地,用IASC-N方法求解第2n+2层,矩阵方程为

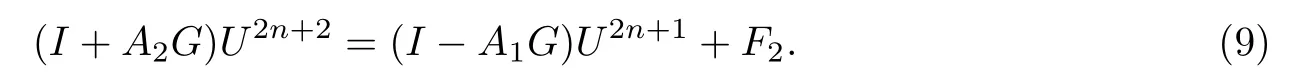
同上分析可得,方程(9)有唯一解.综上分析,有如下定理.

定理1Burgers-Fisher方程IASC-N格式(7)的解是存在且唯一的.

3.2 IASC-N差分格式的线性绝对稳定性

引理3[21]设θ ＞0,矩阵(G+GT)是非负定的,则‖(θI -G)(θI+G)-1‖2≤1.

以下稳定性分析中,假定(7)式中的系数uδ=a为常数且0＜a ＜1.消去Un+1,公式(7)可以改写成Un=GUn-2.其中G为增长矩阵且

对任何偶数n,有

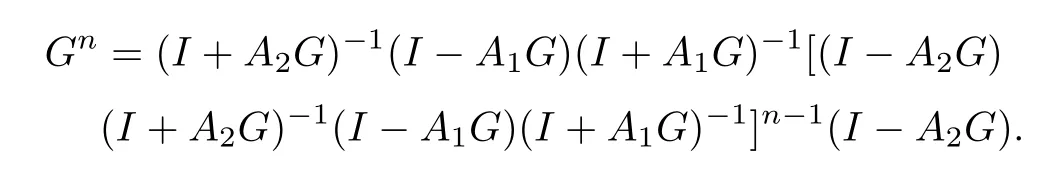
由引理1-3,对任意的r1,r2和r3,有

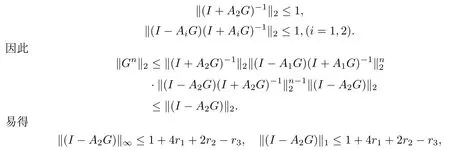
其中r3＜0.因此

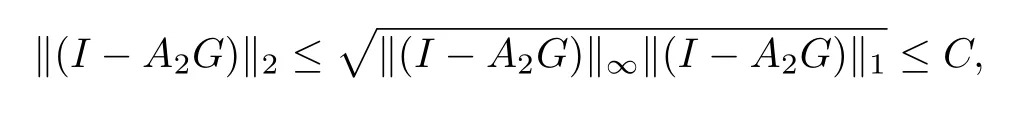
其中C=1+4r1+2r2-r3,即‖Gn‖2≤C.定理得证.

定理2Burgers-Fisher方程的IASC-N格式(7)是线性绝对稳定的.

3.3 IASC-N差分格式的计算精度

古典显式格式:

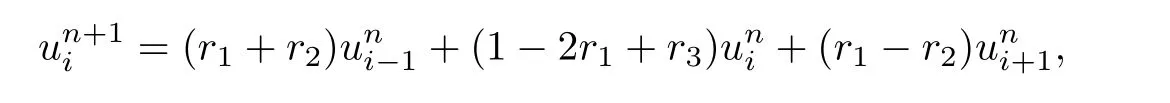
古典隐式格式:

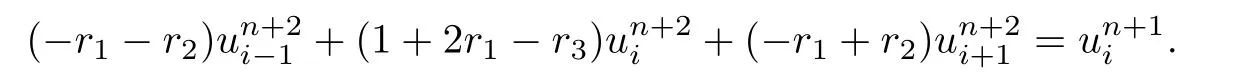
将以上两格式中的各点分别在点un+1i处作Taylor级数展开,记截断误差分别为T1(τ,h),T2(τ,h),则有

由Burgers-Fisher方程IASC-N差分格式的分段化设计可以看出,在每段的“内点”处使用经典的C-N格式,其计算精度为二阶.在每段的“内边界点”处分别使用古典显式格式和古典隐式格式,在T1(τ,h)和T2(τ,h)的表达式中,分别包含了绝对值相同但符号相反的项,古典显式和古典隐式不仅在同一时间层交替进行,在不同时间层也交替进行,部分误差项将相互抵消,因此,IASC-N格式的计算精度为O(h2+τ2).

定理3Burgers-Fisher方程的IASC-N格式(7)计算精度为O(h2+τ2).

3.4 IASC-N差分格式的收敛性

考虑如下非线性方程:

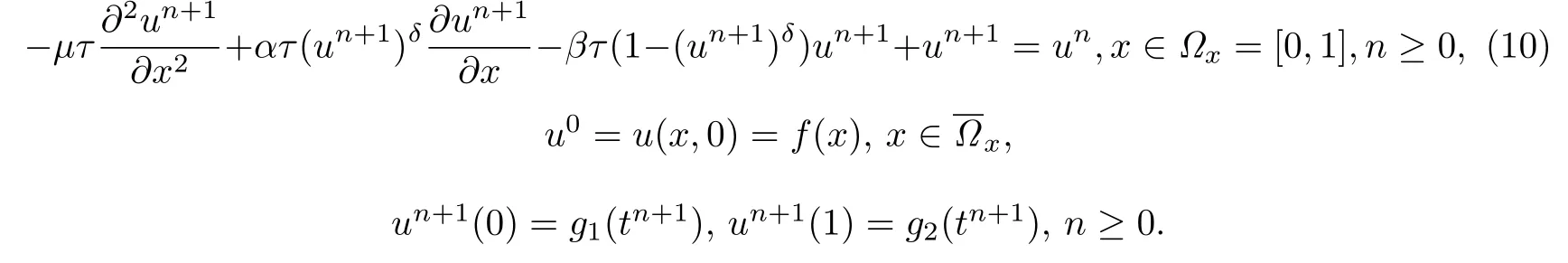
假设u(k)(x)是方程(10)的第k个解,对于非线性方程(10),应用拟线性过程,引入一个由以下递推关系确定的线性方程序列.

其中k=0,1,2,……·是迭代索引.在函数空间,应用Newton-Raphson-Kantorovich近似方法[22],选择一个满足初始条件f(x)的合理初始值u(0)(x).令u(k+1)=得到:

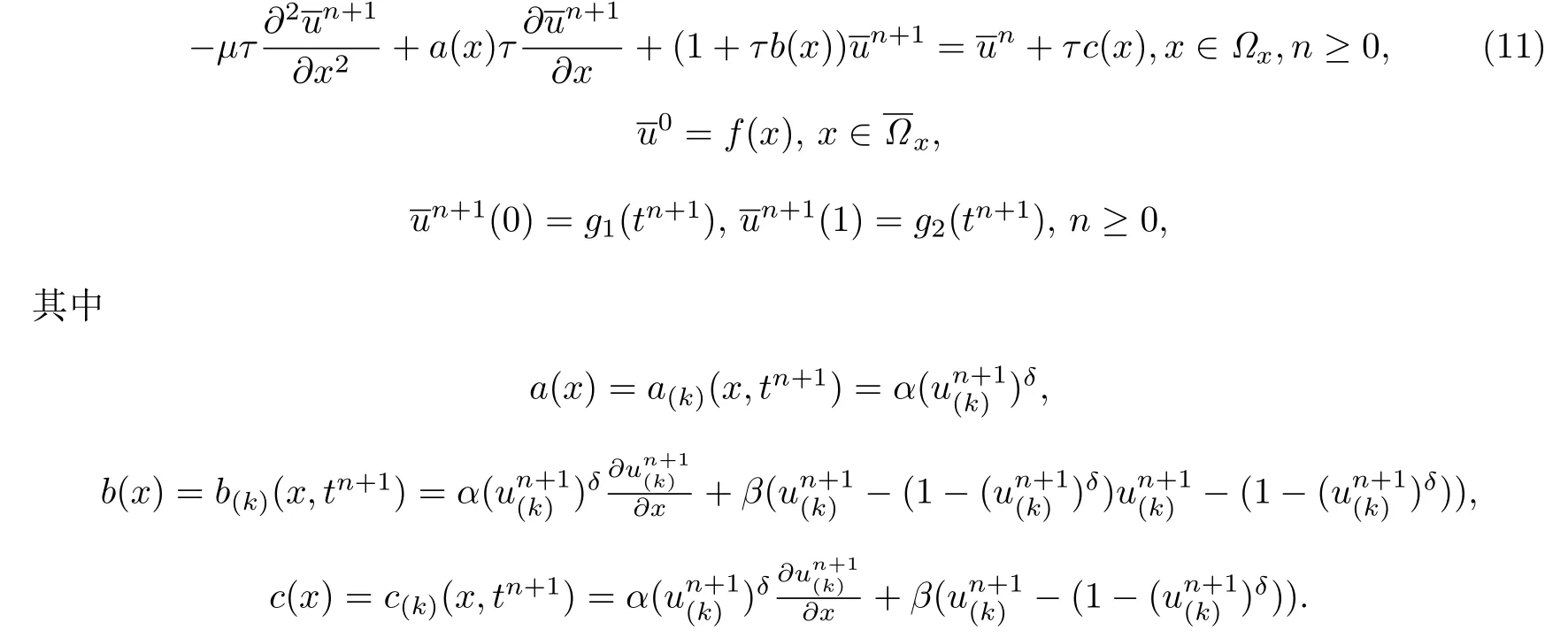
此外,假设函数a(x),b(x)和c(x)是空间方向上足够光滑的函数,且有

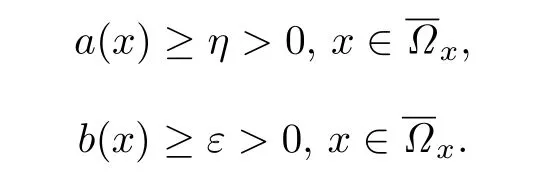
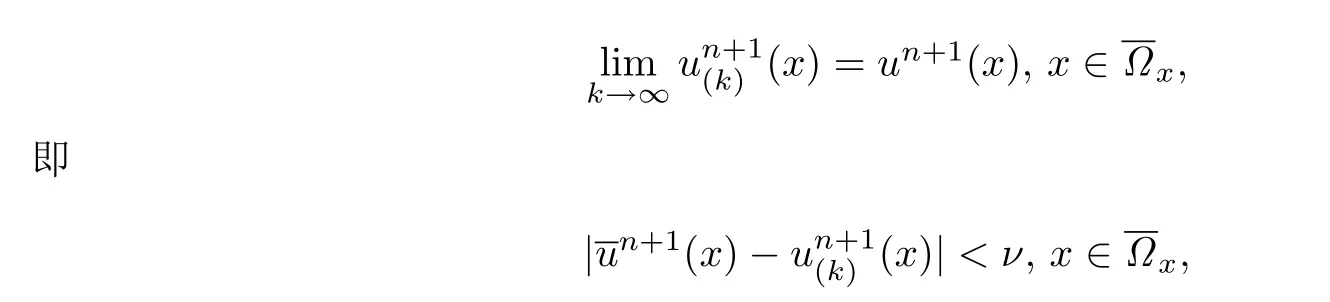
其中ν是终止计算的小规定值.是非线性边值问题(10)的数值解.

在第n+1时间层上,令是由拟线性技术得到的序列.为了证明IASC-N格式的收敛性,考虑以下方程:

通过使用格林函数,将以上方程转化为积分函数

其中格林函数定义如下

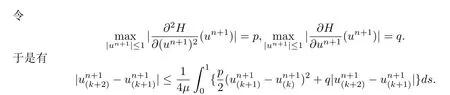
取空间域上的最大范数,简化后得到

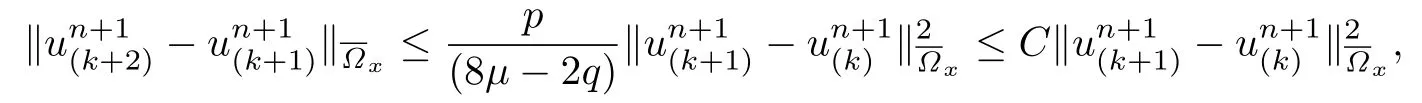
定理得证.

定理4Burgers-Fisher方程的IASC-N格式(7)是收敛的.

§4 数值试验

数值试验基于Intel Core i5-4200 CPU@2.50GHz,四核处理器,在Matlab R2014a环境下运行.

例1取α=0.1,μ=1,β=-0.25,δ=1.考虑如下Burgers-Fisher方程[23]:

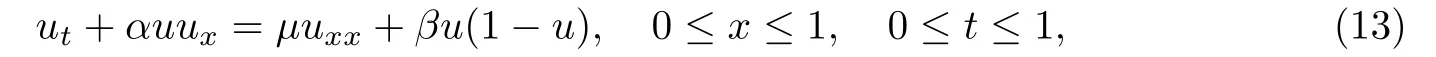
满足以下初边值条件:

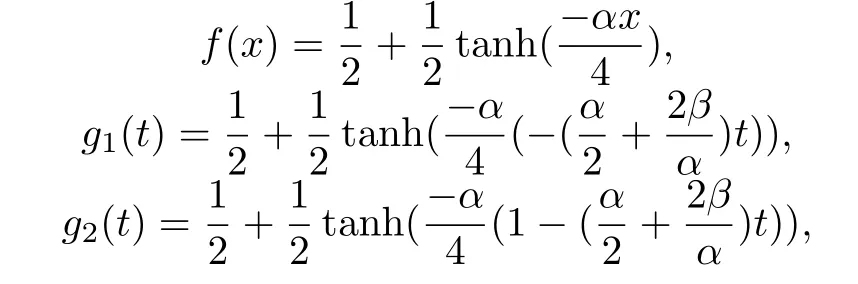
得到解析解为:

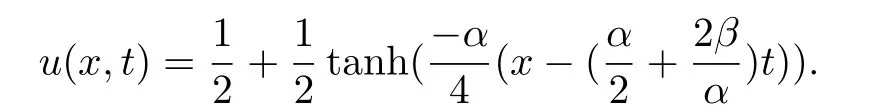
取时间层N=600,空间层M=101,分段数J=5,内点数,解析解曲面,C-N格式解曲面,IASC-N格式解曲面如下.图2至图4可以看出它们的形状整体保持一致.在t=0.5处,将本文IASC-N格式的数值解与解析解,C-N格式解进行比较.计算结果如表1,可以看出IASC-N格式的数值解很好地逼近了解析解,且u的值在0到1之间,符合理论分析.把看作解析解,看作数值解,定义节点误差(Node Error,NE),,图5和图6分别是C-N格式解和IASC-N格式解相对于解析解的节点误差分布图.从图中可以看到,IASC-N格式的计算误差与C-N格式的计算误差相似,且最大误差不超过6e-04.

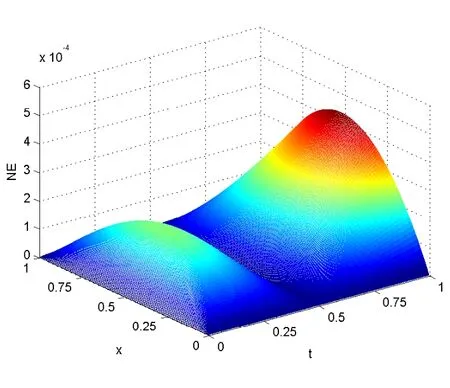
图5 C-N格式解的节点误差分布图

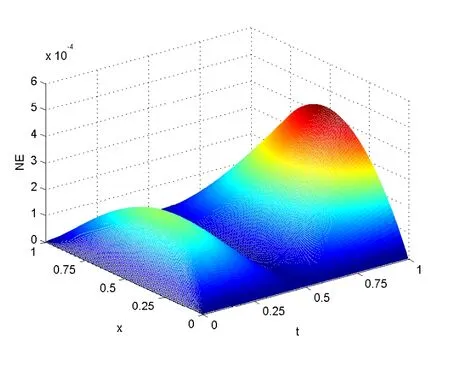
图6 IASC-N格式解的节点误差分布图

表1 数值解与解析解的比较

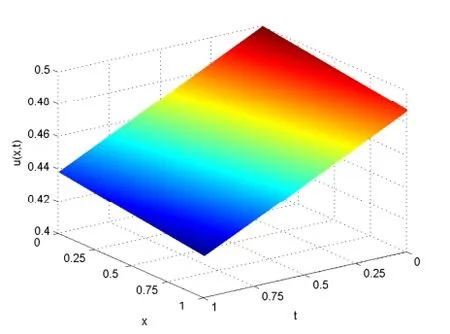
图2 解析解曲面

图3 C-N格式解曲面

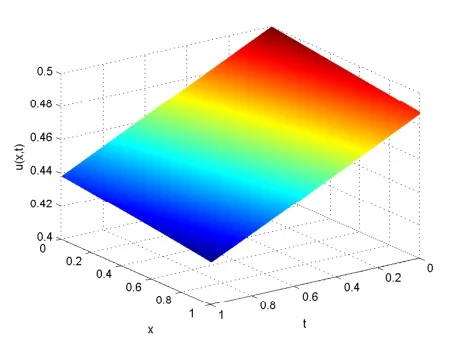
图4 IASC-N格式解曲面

表2和表3分别是取M=601,当N=100,200,300,400,500时,C-N格式解,IASC-N格式解相对于解析解的节点误差.从表中数据可以看出,随着时间层数的增加,当0＜t ≤0.4 时,IASC-N格式解与解析解的节点误差逐渐减小.当0.4＜t ＜1时,IASC-N格式解与解析解的节点误差虽然有少量增加,但都小于C-N格式解与解析解的节点误差,且最大误差均不超过6e-04.说明IASC-N并行差分方法是求解Burgers-Fisher方程的一种高精度差分方法.

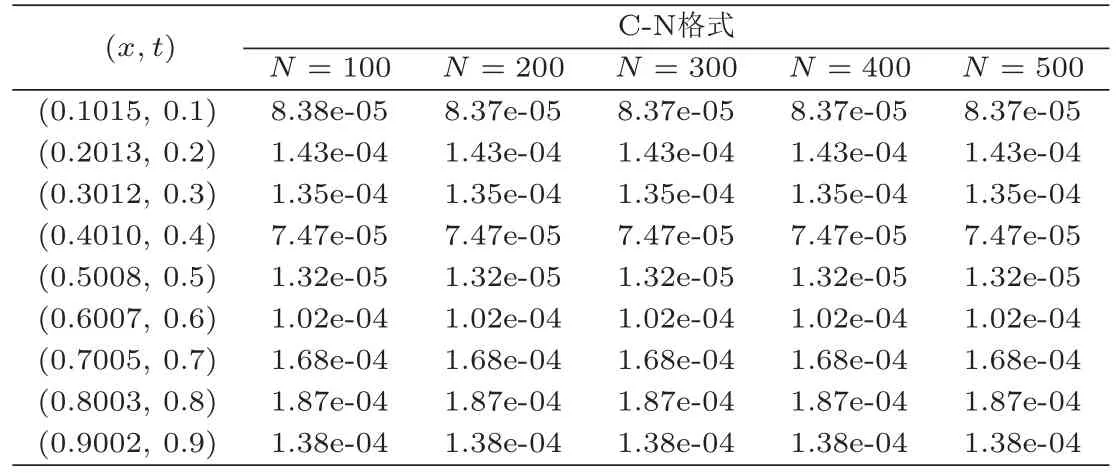
表2 C-N格式解与解析解的节点误差

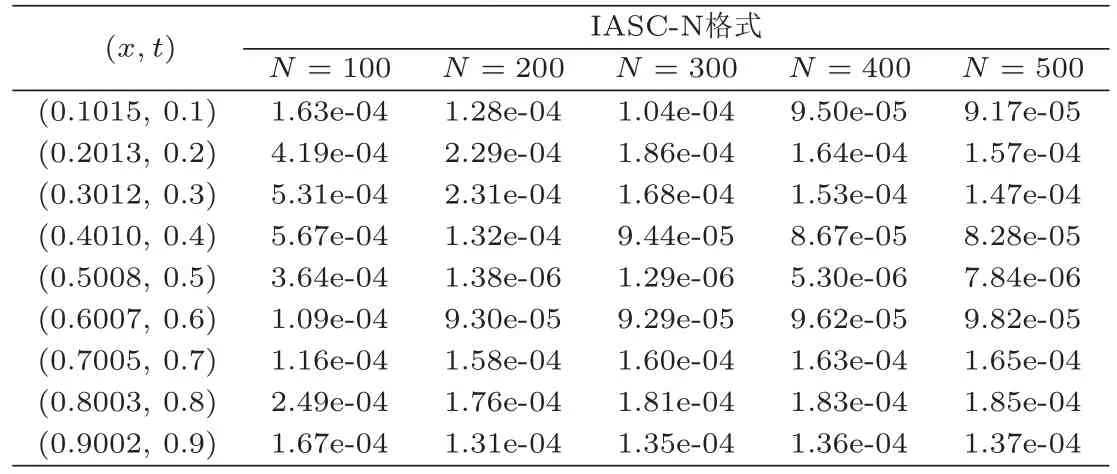
表3 IASC-N格式解与解析解的节点误差

时间收敛阶的计算结果如表4,IASC-N格式在时间方向上的收敛阶接近2阶.从表5可以看到,Orderx的值接近于2.因此得到IASC-N格式的收敛阶是O(h2+τ2).数值结果符合理论分析.

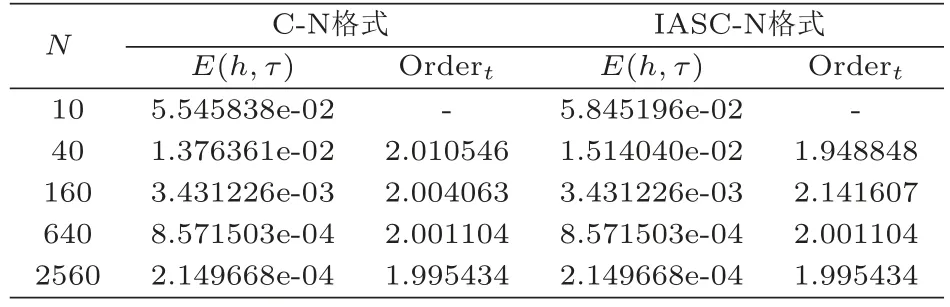
表4 两种格式的数值误差和时间收敛阶

表5 两种格式的数值误差和空间收敛阶

最后,取N=600,当空间网格不断加密时,比较和分析两种格式的计算时间.图7是IASCN格式和C-N格式计算时间的比较.从图中可以看到,当M ＜700时,两格式的计算时间很接近,数据通信对循环产生的影响降低了IASC-N格式的计算效率,并行计算的优越性不明显.但随着网格点数的增加,C-N格式的计算时间迅速增加,而IASC-N格式的计算时间增加缓慢,程序循环体执行的影响远大于数据通信的影响,并行差分格式高效率的优势越来越明显.

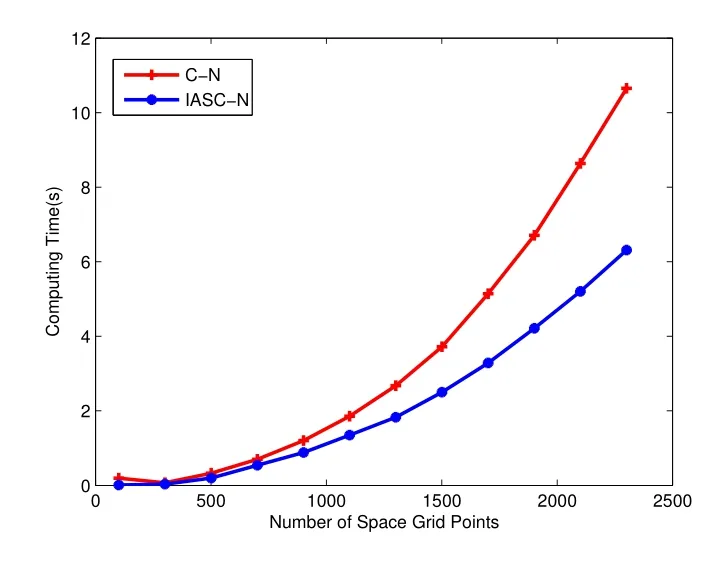
图7 IASC-N格式与C-N格式计算时间比较

比较C-N格式和IASC-N格式的计算速度,定义加速比Sp=T1/Tp和效率Ep=Sp/p(p=4)[26-27].固定时间层N=600,当空间格点数分别为301,701,1101,1501,1901,2301时,两种格式计算时间如表6.

表6 两种格式计算时间及加速比和效率

由表6可以看出,当空间格点数M ＞301时,IASC-N格式的计算时间一直比C-N格式计算时间少,且加速比Sp总是大于1.2.当空间格点数M ＞701时,加速比和效率呈现递增趋势.随着空间格点数的增加,IASC-N格式并行计算的特性更加突出.当空间格点数M ＞1501时,和串行差分格式相比,IASC-N格式的计算时间大约能节约40%.

例2取L=1,T=1,.考虑Burgers-Fisher方程

解析解为

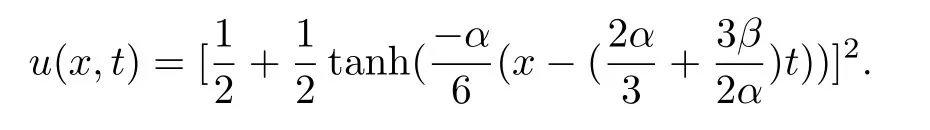
图8是时间层N=600,空间层M=601,t=0.5时,三种格式解的比较,显然IASC-N格式解曲线十分逼近解析解曲线,因此IASC-N并行差分方法是求解Burgers-Fisher方程的一种高精度差分方法.

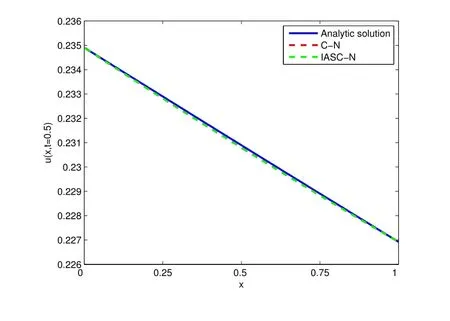
图8 三种格式解的比较

为了验证IASC-N格式的稳定性和计算精度,将解析解看作控制解,C-N格式解和IASCN格式解看作扰动解,定义时间层相对误差和(the Sumof Relative Error for every Time level,SRET)和空间层能量误差(Difference Total Energy,DTE):

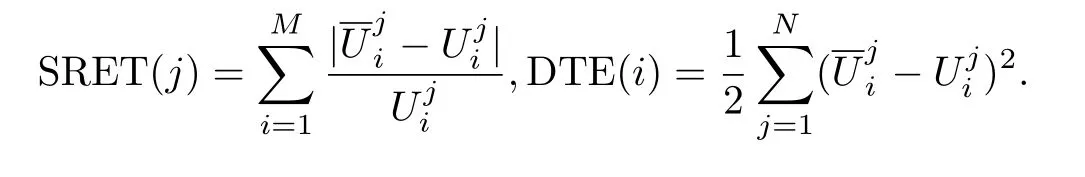
取N=601,M=601,图9可以看出,当时间层数较小时,格式解的误差稍大,但随着时间层数的增加,两种格式解的SRET迅速减小并趋向于0,且IASC-N格式解的SRET始终小于C-N格式解的SRET,说明IASC-N格式是计算稳定的.图10中两种格式的DTE曲线形状相似,且均不超过3e-06,说明IASC-N并行差分方法能够有效求解Burgers-Fisher方程.

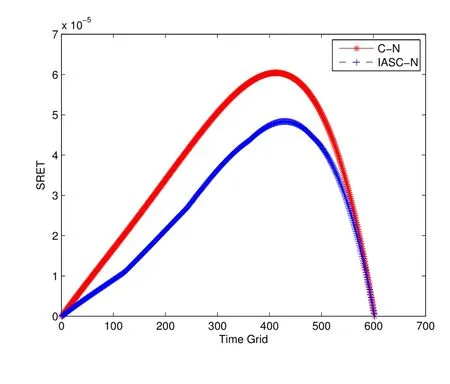
图9 C-N格式解和IASC-N格式解的SRET

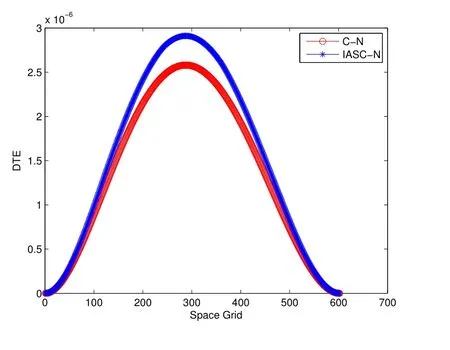
图10 C-N格式解和IASC-N格式解的DTE

§5 结论

本文构造的Burgers-Fisher方程IASC-N并行差分方法是一类典型的离散区域分裂法,既有网格区域分裂也有差分算子分裂.IASC-N并行差分方法是在传统的有限差分理论基础上发展起来的,便于直接地在多种类型的并行计算机上使用.

同时,本文用非线性方程线性化的方法证明IASC-N差分格式的线性绝对稳定性和收敛性.特别当空间分点数足够大时,IASC-N差分格式在计算和通信方面都具有明显的局部化特征,并行特性明显.IASC-N并行差分方法对于求解Burgers-Fisher方程是高效可行的.