单圈图与双圈图补图的Aα-谱半径

张 荣,郭曙光

(盐城师范学院 数学与统计学院,江苏盐城,224002)

§1 引言

本文仅讨论有限无向简单图.G=(V(G),E(G))是n阶连通图,V(G)={v1,v2,……,vn}为其顶点集,E(G)为其边集,dG(vi)表示图G中顶点vi的度,A(G)为G的邻接矩阵,D(G)为G的度对角矩阵.图的无符号拉普拉斯矩阵被定义为Q(G)=D(G)+A(G).2017年,Nikiforov[1]提出并研究图的Aα-矩阵,即图G的度对角矩阵D(G)与邻接矩阵A(G)的凸线性组合:

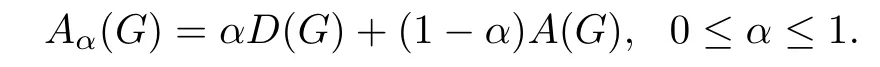
称它的最大特征根为G的Aα-谱半径,简记为ρα(G).若G为连通图,则Aα(G)是不可约的.根据非负矩阵的Perron-Frobenius定理,ρα(G) 的重数为1,并且存在唯一的正单位特征向量,称之为ρα(G)的Perron向量.图G的补图Gc是指与G有相同顶点集的简单图,在Gc中两个顶点相邻当且仅当它们在G中不相邻.

1986年,Brualdi和Solheid[2]提出了确定图类邻接谱半径的界并刻画极图的问题.这类问题后来被称为Brualdi-Solheid问题,被人们广泛研究,并被移植到各种图矩阵的谱半径研究中,至今仍然是图谱研究的热点.2014年,Stevanovi´c的新著[3]对近十年来邻接谱半径(特别是Brualdi-Solheid问题)的研究成果,证明技巧进行了综述,并提出一些值得进一步研究的猜想和待解决问题.2017年,Tait和Tobin[4]在n充分大的前提下证明了Brualdi-Solheid型问题的三个著名猜想,2018年,Bollobás等人[5]研究了d维超方体图的m阶导出子图谱半径的最大化问题.

图的Aα-矩阵统一并推广了邻接矩阵与无符号拉普拉斯矩阵,对它的研究可将邻接谱和无符号拉普拉斯谱的研究方法一般化,得到一般性的结果,因而成为近期图谱研究的又一热点.图的Aα-谱半径的Brualdi-Solheid问题更是受到研究者的广泛关注.例如,Nikiforov[1]分别确定了色数给定和不含Kr+1(r ≥2)图的Aα-谱半径的可达上界.Nikiforov等[6]给出最大度给定的树的Aα-谱半径一个紧的上界.Nikiforov等[7]和Xue等[8]同时确定了直径给定的图的Aα-谱半径最大的图和团数给定的图的Aα-谱半径最小的图.Lin等[9]分别确定了割点数给定的连通图和匹配数给定的树的Aα-谱半径最大的图.Li等[10]分别确定了给定度序列的n阶树和单圈图的Aα-谱半径最大的图.Yu等[11]给出了不含K2,t(t ≥3) minor的图Aα-谱半径可达上界,并确定了具有最大Aα-谱半径的唯一的外平面图.Chen等[12]给出了一个图的二次幂图的Aα-谱半径的上界和下界,并确定了树的二次幂图的Aα-谱半径前三大的图.

边数等于顶点数加c-1的简单连通图称为c圈图.当c=0,1,2,3 时,分别称之为树,单圈图,双圈图,三圈图.Liu等[13]给出了n阶单圈图的补图的邻接谱半径的上界,并刻画了唯一的达到该上界的极图.Yin等[14]给出了n阶三圈图的补图的邻接谱半径的上界,并刻画了唯一的达到该上界的极图.本文研究单圈图与双圈图补图的Aα-谱半径,分别确定n阶单圈图与双圈图补图的Aα-谱半径的上界,并刻画相应的极图.

§2 记号与引理

用Cn表示n个顶点的圈,Pn表示n个顶点的路,Kn表示n个顶点的完全图,Nn表示n个顶点的空图,NG(v)表示图G中邻接于v的顶点组成的集合.G的悬挂顶点是指度为1的顶点,与悬挂顶点相关联的边称为悬挂边.若S ⊆V(G),用G[S]表示图G的由S导出的子图.两个图G1=(V1,E1)和G2=(V2,E2)(V1∩V2=∅)的直和是指图G=G1∪G2,其中V(G)=V1∪V2,E(G)=E1∪E2.图G1=(V1,E1)与G2=(V2,E2)的完全积记为G1▽G2,是指把G1∪G2中的V1的每一个顶点分别与V2的每一个顶点连接所得到的图.设x=(x1,x2,……,xn)T为n维单位实列向量,根据Rayleigh’s准则[15]知

其中等号成立当且仅当x为对应于ρα(G)的特征向量.

引理2.1[7-8]设α ∈[0,1),G为连通图,u,w是G的两个顶点,uvi ∈E(G)且wvi/∈E(G)(i=1,2,……,k).设x=(x1,x2,……,xn)T为对应于ρα(G)的Perron向量.令G*为从G中删除边uvi并加上边wvi(i=1,2,……,k)得到的图.若xw ≥xu,则ρα(G*)＞ρα(G).

引理2.2[16]设0≤α ≤1,G是一个图,S ⊆V(G)且|S|=k.若对任意w ∈S,有dG(w)=d且对任意u,v ∈S满足N(v){u}=N(u){v},则有下面的结论成立.

(1) 如果G[S]是一个团,则(d+1)α-1是Aα(G)的一个特征值,其重数至少为k-1.

(2) 如果G[S]是一个独立集,则dα是Aα(G)的一个特征值,其重数至少为k-1.

下面的引理是引理2.1的一个推论,它是主要结果证明的关键.

根据引理2.3,可证明下列引理.

引理2.4设uv是图G的一条非悬挂边的割边,并且Gc也是连通图,记收缩边uv成一点w并在点w接出一条悬挂边所得的图为G*(如图1所示),则ρα(Gc)＜ρα(G*c).

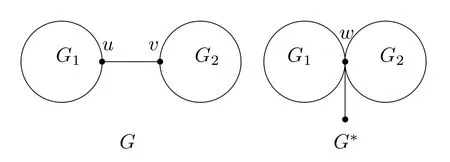
图1 G,G*

设G1,G2为两个连通图,u1,u2分别是它们的顶点.将G1中的顶点u1和G2中的顶点u2粘合成一个顶点,所得的图记为G1u1u2G2(简记为G1G2).特别地,GTn(如图2所示)表示将图G的一个顶点与一棵n阶树Tn的一个顶点粘合所得图.GK1,n-1(如图2所示)将图G的一个顶点与K1,n-1的中心粘合所得的图.

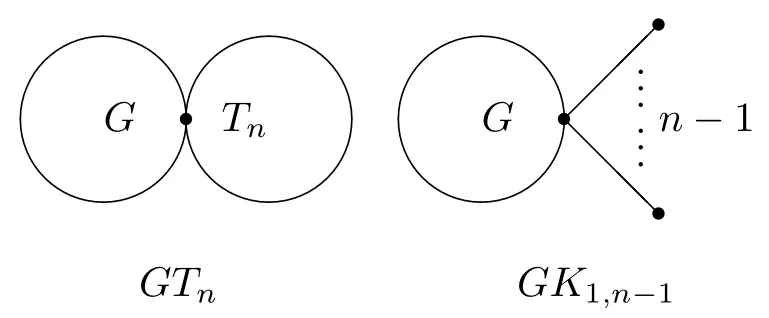
图2 GTn,GK1,n-1

§3 单圈图补图的Aα-谱半径

综合引理3.1和引理3.2,可以得到下述结论.

定理3.1设0≤α ＜1,图G为n阶单圈图,则

§4 双圈图补图的Aα-谱半径

用B(n)表示所有n阶双圈图组成的集合.令Ck,Cl是两个顶点不相交的圈,v1是Ck的一个顶点,vs是Cl的一个顶点.把v1和vs用长为s-1 (s ≥1)的路v1v2……·vs连接起来所得到的图称为∞-图(如图3所示),其中s=1表示把v1,vs重合到一起.令Pl+1,Pp+1,Pq+1(l,p,q ≥1)是三条顶点不相交的路,并且其中至多有一条路的长为1.把这三条路的起始顶点和终点分别重合到一起所得到的图称为θ-图(如图3所示).双圈图可分为两类,一类记为Bn,1,其中的图要么是一个n阶∞-图,要么是在∞-图的某些顶点接出一些树得到的n阶图;另一类记为Bn,2,其中的图要么是一个n阶θ-图,要么是在θ-图的某些顶点接出一些树得到的n阶图.

图3 ∞-图, θ-图

设B1与B2是如图4所示的两个n阶双圈图.当n ＞5时,不难看出,除B1和B2之外,其它所有n阶双圈图的补图均为连通图.当n ＞5时,类似于单圈图补图的Aα-谱半径的证明过程,可以得到如下结论.当n=5 时通过直接计算验证如下结论成立.

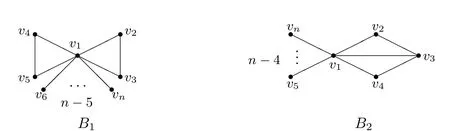
图4 B1, B2

引理4.1设0≤α ＜1,G ∈Bn,1,则ρα(Gc)≤ρα(B1c),其中等号成立当且仅当G～=B1.

引理4.2设0≤α ＜1,G ∈Bn,2,则ρα(Gc)≤ρα(B2c),其中等号成立当且仅当G～=B2.

对于n阶双圈图,在引理4.1和引理4.2的基础上,可以证明下述定理.

致谢衷心感谢审稿人的意见和建议.