具有时滞和体液免疫反应的宿主体内登革热感染模型的稳定性和Hopf分支

王海峰,田晓红

(山西大学复杂系统研究所,山西太原 030006)

§1 引言

登革热是由登革热病毒引发的,主要由埃及伊蚊和白纹伊蚊传播的一种媒介传染病,广泛流行于热带和亚热带地区.近年来,在我国两广等地区几乎每年都会发生不同程度的流行[1].2009年,WHO将有症状的登革热病毒感染简单分为轻症登革热病毒和重症登革热,而后者被认为与二次异型登革热病毒感染,病毒变异和宿主免疫反应等因素有关[2].文[3]中指出,宿主感染登革热后会诱导体内细胞启动一系列免疫反应,如树突状细胞和自然杀伤细胞被激活,并与其他免疫细胞协同作用,以激活机体不同的免疫防御功能.人类免疫系统由先天性免疫应答和适应性免疫应答两部分组成,其中适应性免疫系统产生分泌抗体的B细胞(体液免疫应答)和细胞毒性T细胞(细胞介导的免疫应答),两者既各自有独特的作用,又可以相互配合,共同发挥免疫效应.

文[4]中,Sulanie Perera和SSN Perera建立了一类具有体液免疫应答的登革热模型:

其中δ=1-e-mt表示抗体产生的时滞,这里m为常数.S(t),I(t)和V(t)分别表示t时刻易感细胞,感染细胞和游离病毒的浓度,Z(t)表示t时刻的体液免疫反应(B细胞或抗体的浓度).参数Λ,β,d,a,k,p,u,η,c和b都是正常数,易感细胞以常数速率Λ产生且以速率dS死亡,受到游离病毒感染后,以速率βSV变成感染细胞,这里β表示传染率.感染细胞以速率aI死亡,以速率kI裂解产生游离病毒.游离病毒以速率uV死亡且以速率pZV被抗体清除,这里p表示抗体对游离病毒的清除率.βSV这一项表示病毒在感染易感细胞时因被吸收而导致病毒在血液中减少的数目.免疫B细胞以常数速率γ产生且以速率bZ死亡,且当免疫系统受到游离病毒刺激后,以速率cZV产生免疫B细胞,这里c表示游离病毒对免疫B细胞的作用率.在文[4]中,通过分析特征方程仅讨论了当γ=0时病毒感染平衡点的局部稳定性.

近年来,考虑宿主免疫反应的登革热模型的研究已经引起许多学者的关注.文[5]中,Nuraini等建立了具有细胞免疫的单核细胞群登革热病毒感染动力学模型.结果表明,随着病毒入侵速度的增加,游离病毒数量呈下降趋势,免疫反应可显著降低模型的基本再生率.文[6]中,Ansari和Hesaaraki引入非线性感染率来描述病毒的感染过程,建立了一类具有Beddington-De-Angelis感染率和细胞免疫的登革热病毒传播模型.注意到,在上述研究中都忽略了时滞对模型动力学性态的影响.事实上,正如文[7]中所指出,机体内的免疫系统从接受病毒刺激到产生免疫B细胞需要一段时间.

基于文献[4,7]的工作,本文研究如下具有时滞和体液免疫的宿主体内登革热感染模型:

其中τ表示机体内的免疫系统从接受病毒刺激到产生免疫B细胞所需要的时间.

系统(2)的初始条件为

由泛函微分方程的基本理论[8]知,系统(2)存在满足条件(3)的唯一解(S(t),I(t),V(t),Z(t)).容易验证,系统(2)满足初始条件(3)的所有解在区间[0,∞)上有定义,且对所有的t≥0恒为正.

§2 局部稳定性和Hopf分支

本节证明系统(2)满足初始条件(3)的正解是有界的,并通过分析相应特征方程根的分布讨论系统(2)可行平衡点的局部渐近稳定性.

定理2.1对于任意的t≥0,系统(2)满足初始条件(3)的正解有界.

证 设(S(t),I(t),V(t),Z(t))是系统(2)满足初始条件(3)的任一正解.令

将B1(t)沿着系统(2)求导可得

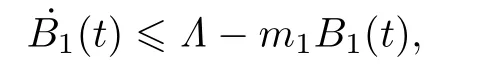
这里m1=min{a,d}.于是有

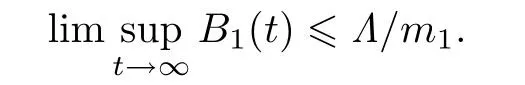
因此可知S(t)和I(t)在t ∈[0,∞)上有界.进一步将B2(t)沿着系统(2)求导可得

这里m2=min{a,b,u}和¯I=max{I(t):t ∈[0,∞)}.于是有

由此可知V(t)和Z(t)在t ∈[0,∞)上有界.

易知系统(2)存在未感染平衡点E0(Λ/d,0,0,η/b).由下一代矩阵方法[9]可算得相应的下一代矩阵为

则系统(2)的基本再生数为

这里R0表示在感染初期一个感染细胞所能产生的感染细胞的数量.

当R0＞1时,容易验证不等式

成立,这里Δ=(cβ(k-a)Λ+aβ(pη-bu)-acdu)2+4aβuη(abpβ+acdp).因此,当R0＞1时,除未感染平衡点E0外,系统(2)还存在唯一的免疫激活感染平衡点E*(S*,I*,V *,Z*),其中

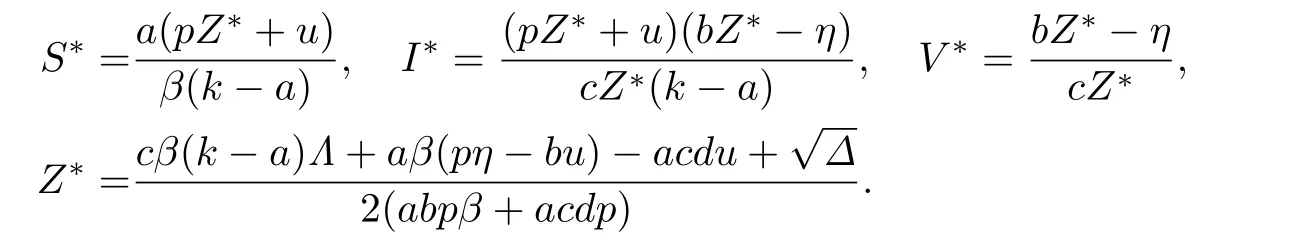
定理2.2如果R0＜1,系统(2)的未感染平衡点E0(Λ/d,0,0,η/b)是局部渐近稳定的;如果R0＞1,则E0不稳定.

证系统(2)在未感染平衡点E0处的特征方程为

显然,方程(4)总有两个负实根:λ1=-b ＜0,λ2=-d ＜0.其余的根由如下方程

确定.容易验证,当R0＜1时,有

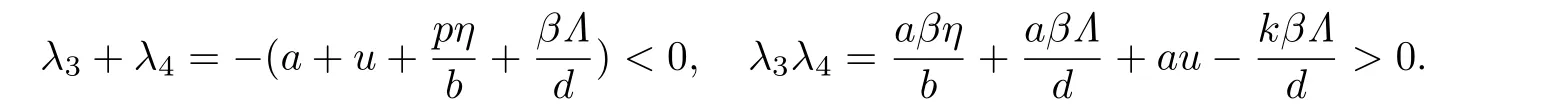
此时λ3,λ4＜0,故(4)所有的根均具有负实部.因此当R0＜1时,未感染平衡点E0(Λ/d,0,0,η/b)是局部渐近稳定的.当R0＞1时,方程(5)至少有一个正实根,故E0不稳定.

系统(2)在免疫激活感染平衡点E*处的特征方程为

当τ=0时,方程(6)变为

经过计算可知

因此,由Routh-Hurwitz判据[10]可知,当τ=0时,免疫激活感染平衡点E*(S*,I*,V *,Z*)是局部渐近稳定的.

当τ ＞0时,设λ=iω是方程(6)的根,将其代入到(6)并分离实部虚部可得

将(8)的两个方程分别平方后再相加得到

令z=ω2,则方程(9)可化为

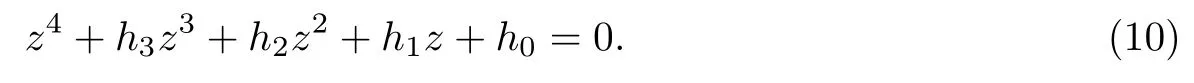
记h(z)=z4+h3z3+h2z2+h1z+h0,则

令z=y-h3/4,则由(11)可得y3+Py+Q=0,其中

从而,由一元三次方程求根公式(卡丹公式)可知方程(11)最大实根为

因此,应用与文献[11]中类似的讨论,有

引理2.1对于方程(10)有下述结论成立:

(i) 如果h0＜0,则方程(10)至少有一个正实根.

(ii) 如果h0≥0,下述条件之一成立时,则方程(10)无正根:

经计算可得

为不失一般性,不妨设方程(10)有三个正实根为z1,z2,z3,那么相应的方程(9)也有三个正实根.由方程(8)可得

其中k=1,2,3;j=0,1,2,....记是方程(7)关于的一对纯虚根.定义

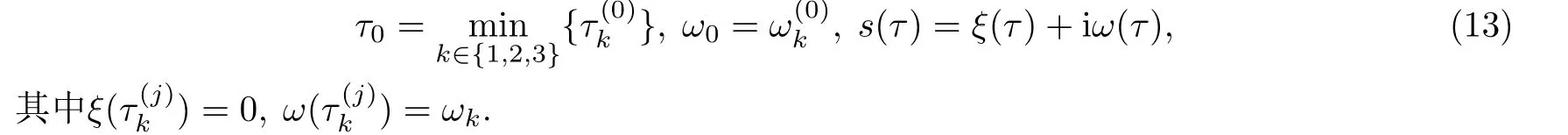
将(6)两端对τ求导整理可得

因为zk ＞0,因此有时与h′(zk)同号.

定理2.3假设和ω0,τ0分别由(12)和(13)所定义.当R0＞1时,

(i) 如果h0≥0且下列条件之一成立,

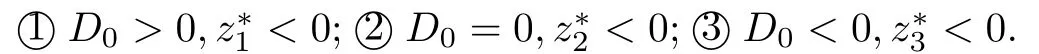
则对所有的τ≥0,系统(2)的免疫激活感染平衡点E*是局部渐近稳定的.

(ii) 如果h0＜0或h0≥0且下列条件之一成立,

则对于任意的τ ∈[0,τ0),免疫激活感染平衡点E*是局部渐近稳定的.

§3 全局渐近稳定

本节将分别讨论系统(2)未感染平衡点E0(Λ/d,0,0,η/b)和免疫激活感染平衡点E*(S*,I*,V *,Z*)的全局渐近稳定性.

定理3.1当R0＜1时,系统(2)的未感染平衡点E0(Λ/d,0,0,η/b)是全局渐近稳定的.

证 设(S(t),I(t),V(t),Z(t))是系统(2)满足初始条件(3)的任一正解.

记S0=Λ/d,Z0=η/b.由系统(2)第四个方程可知

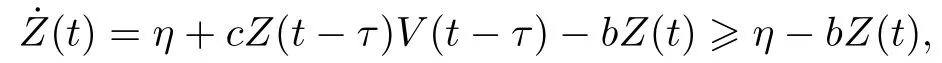
则有lim inft→∞Z(t)≥Z0,即对任意充分小的∈＞0,存在T ＞0,当t ＞T时,有Z(t)＞Z0-∈.

定义Lyapunov函数为

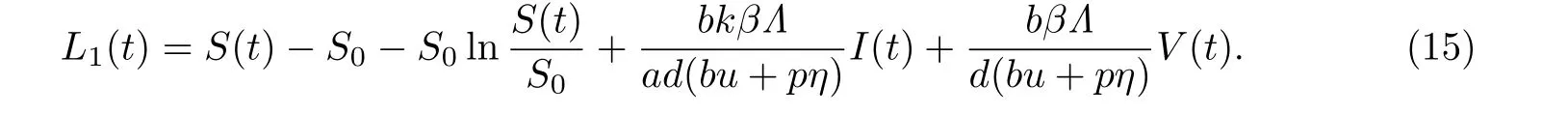
计算L1(t)沿系统(2)解的全导数可得

显然当R0＜1时,(t)≤0,当且仅当S=S0,V=0时,(t)=0.进一步由系统(2)的第二和四个方程可得I=0,Z=Z0.因此未感染平衡点E0的最大不变集为

由Lyapunov-LaSalle不变性原理可知,当R0＜1时,未感染平衡点E0是全局渐近稳定的.

定理3.2假设τ=0.当R0＞1时,若下列条件

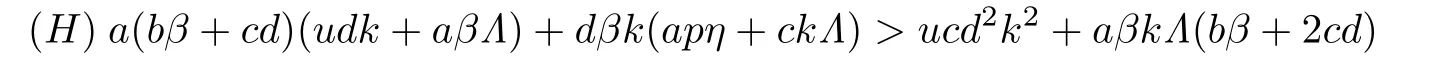
成立,则系统(2)的免疫激活感染平衡点E*(S*,I*,V *,Z*)是全局渐近稳定的.

证设S(t),I(t),V(t),Z(t)是系统(2)满足初始条件(3)的任一正解.定义Lyapunov函数为

计算L2(t)沿系统(2)解的全导数可得

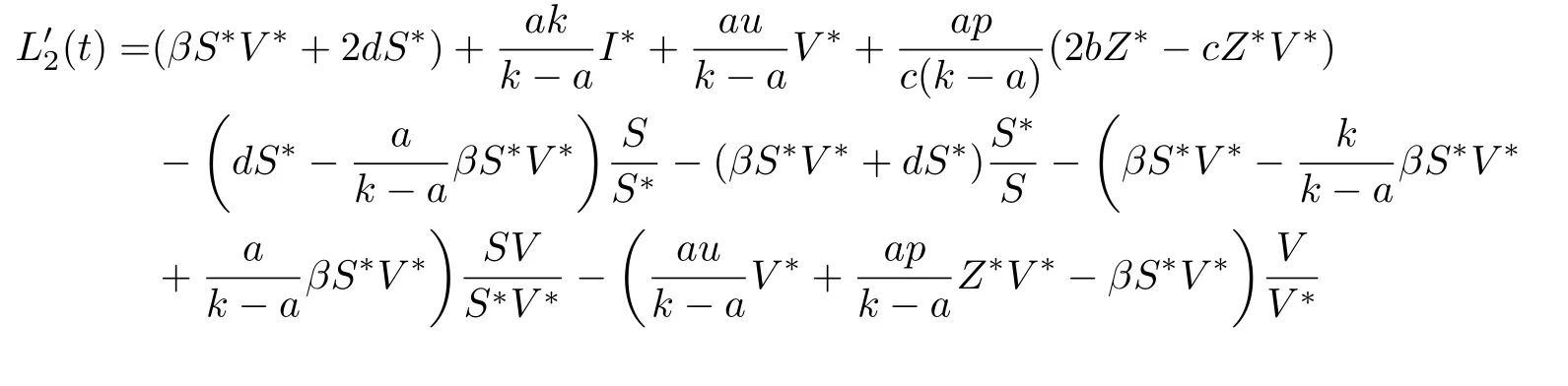
本节通过数值模拟来说明所得理论结果的可行性.

在系统(2)中,相应参数取值如表1所示,经过计算得到R0≈3.3＞1,此时系统(2)存在一个免疫激活感染平衡点E*(137.7104,4.4493,7.5388,812.6021).进一步计算可知h0=-6.24×10-6＜0,z1=0.0270,h′(z1)=0.0157/=0,ω0=0.1643,τ0=2.9333,由定理2.3可知,当τ=2＜τ0时,免疫激活感染平衡点E*是局部渐近稳定的;当τ=3.5＞τ0时,E*不稳定;当τ=τ0时,系统(2)在E*附近将出现Hopf分支(见图1,2).

表1 登革热感染模型(2)的参数值

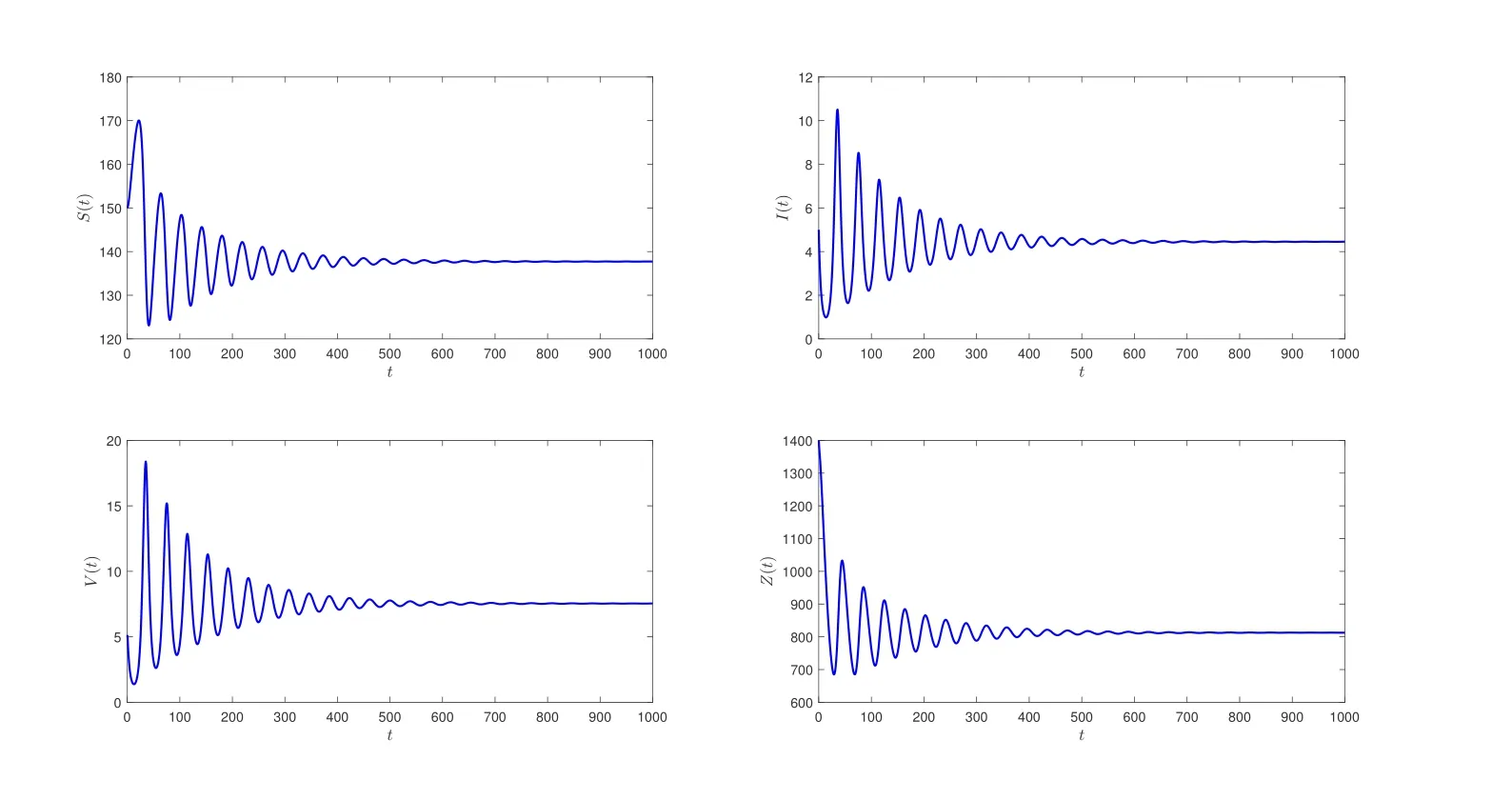
图1 初始条件(φ1,φ2,φ3,φ4)≡(150,5,5,1400),当τ=2 ＜τ0时,系统(2)的免疫激活感染平衡点E*局部渐近稳定

由算术平均值和几何平均值的关系可知

当条件(H)成立时,经过计算可知Λ ＞akI*/(k -a).由此,当τ=0时,若R0＞1且(H)成立,则(t) ≤0,当且仅当S=S*,I=I*,V=V *,Z=Z*,有(t)=0.于是由Lyapunov-LaSalle不变性原理可知,E*是全局渐近稳定的.

§4 数值模拟

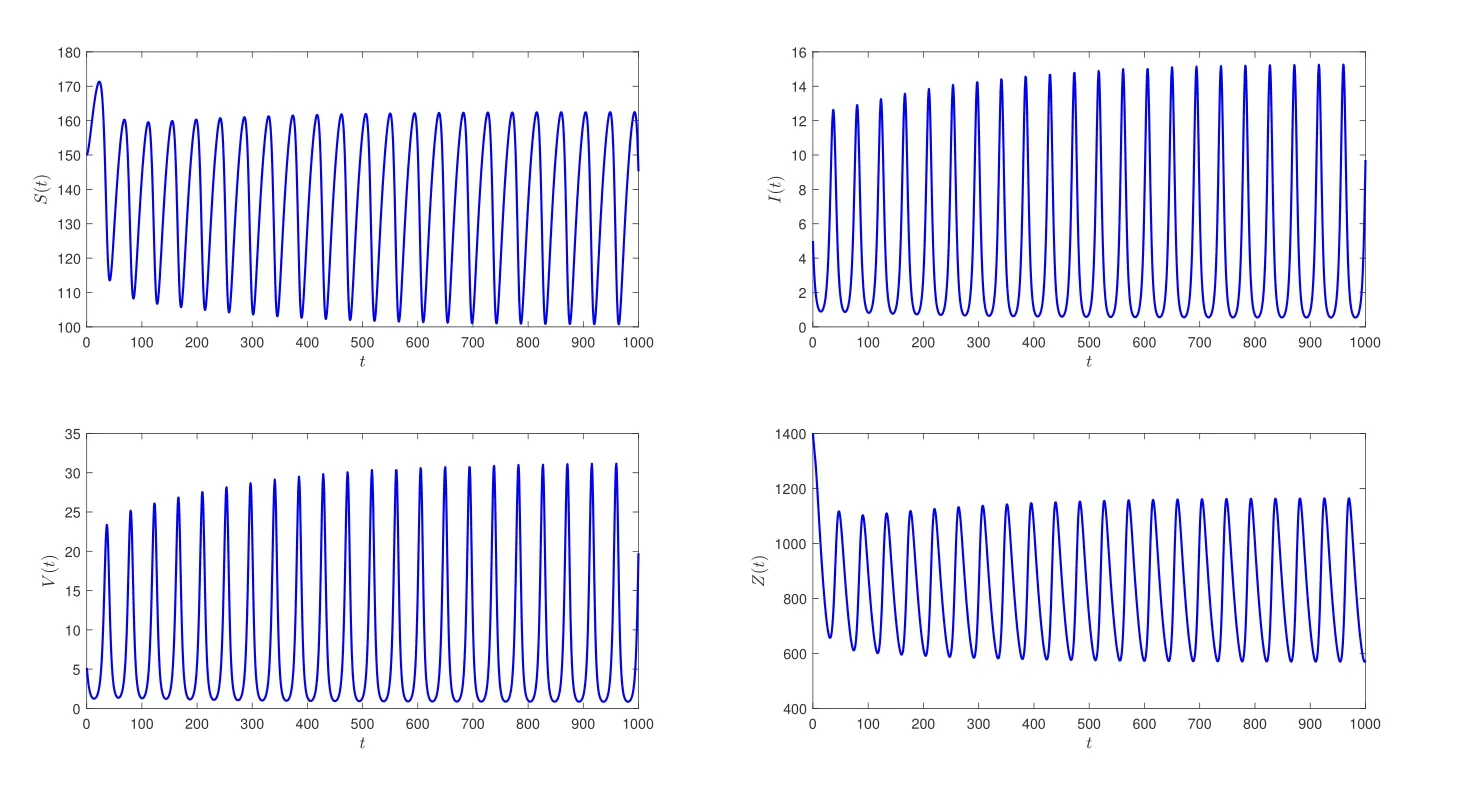
图2 初始条件(φ1,φ2,φ3,φ4)≡(150,5,5,1400),当τ=3.5 ＞τ0时,系统(2)的免疫激活感染平衡点E*失去稳定性,且出现了Hopf分支

§5 结论

通过对系统(2)的研究,本文分析了具有时滞和体液免疫反应的宿主体内登革热感染模型的稳定性与Hopf分支.通过分析相应的特征方程,得到了每个可行平衡点的局部稳定性和Hopf分支的存在性.根据定理2.3,可以看到当时滞增加超过临界值时,免疫激活感染平衡点的稳定性发生了改变,系统在E*处发生了Hopf分支.通过构造适当的Lyapunov函数并利用LaSalle不变性原理,证明了系统(2)未感染平衡点的全局稳定性并给出了免疫激活感染平衡点全局稳定的充分条件.由定理3.1可知当R0＜1时,未感染平衡点E0是全局渐近稳定.此时,病毒将会被清除.由定理3.2可知当R0＞1且时滞为0时,若条件(H)成立,则免疫激活感染平衡点E*是全局渐近稳定的.在这种情况下,感染会变成具有抗体免疫反应的慢性感染.

注意到文献[4]中,Sulanie Perera和SSN Perera仅分析了当γ=0时病毒感染平衡点的局部稳定性.本文拓展了文献[4]的模型,考虑了更一般的情形γ/=0(即η/=0),且综合考虑了免疫时滞的影响.本文的研究成果表明在一定条件下,时滞将会破坏其系统原有的稳定性,进一步呈现出复杂的动力学行为.此外,只针对τ=0时讨论了病毒感染平衡点E*的全局稳定性.当τ ＞0时,病毒感染平衡点E*全局稳定性的研究将在今后的工作中进一步讨论.