射影几何观点下圆切线作法的理论研究与应用

况周炜，赵临龙

(安康学院数学与统计学院，陕西 安康 725000)

1 问题背景

射影几何是研究二次曲线几何性的重要方法，比如对二阶曲线过其外一点作切线就可以通过极点与极线的关系来实现[1]。而对于二次曲线特殊的圆，欧氏几何中也存在过其外一点作切线[2-4]，其作图方法与射影几何作图法有所不同，两者之间是否存在联系值得讨论。

2 二阶曲线切线的射影几何作图

问题1：已知二阶曲线Γ及不在Γ上的一点P，求作点P关于二阶曲线Γ的切线。

作法：如图1。

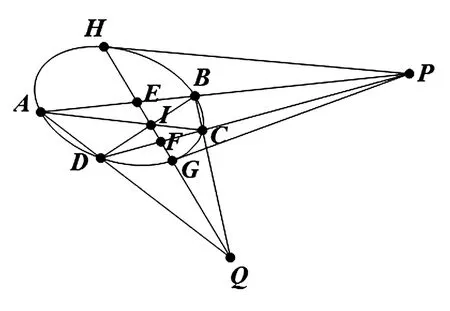
图1

①过点P作过二阶曲线Γ的两条割线与二阶曲线Γ分别交于点A、B、C、D。

②连接AD、BC交于点Q。

③连接AC、BD交于点I。

④作过Q、I的直线交二阶曲线Γ于点H、G。

⑤连接PH、PG，则PH、PG就为二阶曲线Γ的切线。

证明：∵ABCD为完全四点形，而且PQI为完全四点形ABCD的对边三点形，∴(AB,PE)=-1,(CD,PF)=-1，∴E、F为二阶曲线Γ的调和共轭点，所以HQ为点P的极线，即PH、PG为二阶曲线Γ的切线。

3 圆的欧氏几何作图

问题2：已知圆与圆外任意一点P，作过点P关于圆的切线。

作法：如图2。

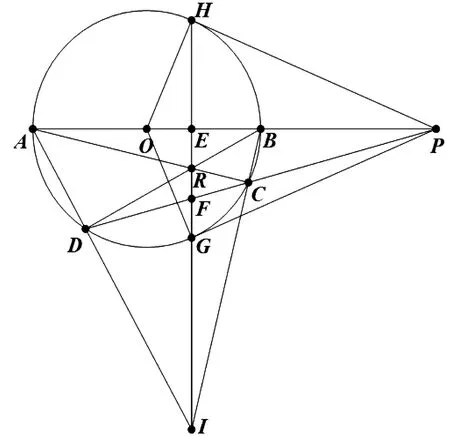
图2

①过点P作过圆的两条割线与圆分别交于点A、B、C、D且割线PAB过圆心。

②连接AD、BC交于点I。

③连接AC、BD交于点R。

④作过R、I的直线交圆于点H、G。

⑤连接PG、PH，则PH、PG就是圆的切线。

证明：连接OP交HG于点E，连接OH、OG。

(1)

(2)

则(AO+OE)(PO-OB)=(OB-OE)(PO+OA)

∴(OH)2=(OG)2=OE·OP，∴PH、PG为圆的切线。

可见，过圆外任意一点P作其圆的切线都可以利用射影几何方法来实现，但对于特殊的圆要用到圆的直径，能够将圆与二次曲线过其外任意一点P作其切线统一起来。

4 圆作切线的应用

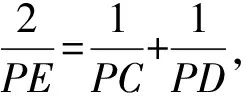
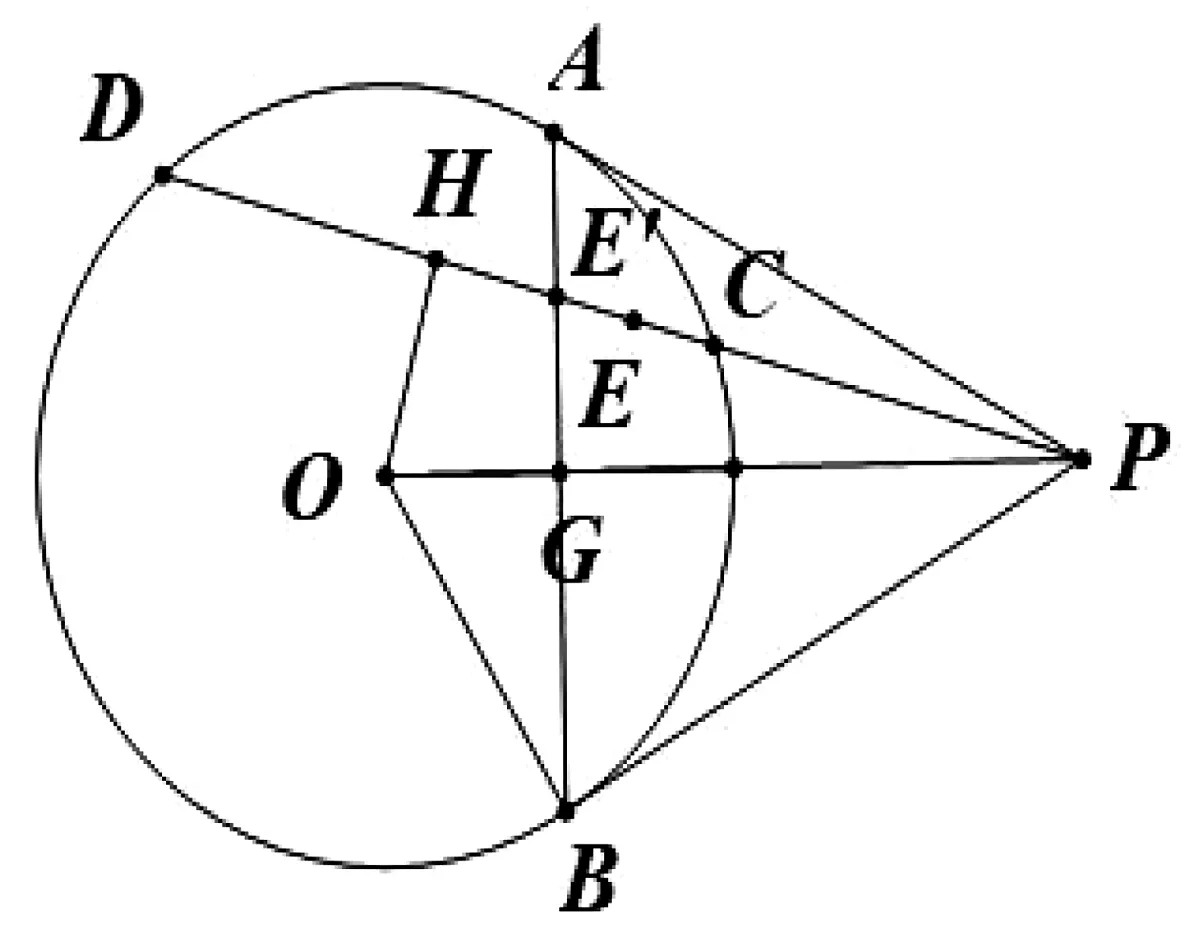
图3

证明：连接OP、OA，OP与AB交于点G，作OH⊥CD，垂足为点H。设AB交PD于点E′，则∠OHP=∠OGA=90°，∴OGE′H四点共圆，∴PE′·PH=PG·PO

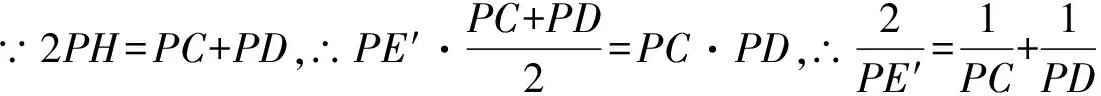
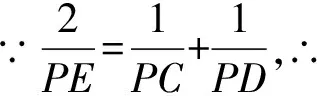
在命题1中，极点P与极线AB的调和共轭点关系为(CD,PE)=-1。

由此得到命题。

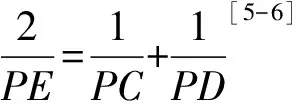
命题2是根据2001年TI杯全国初中数学竞赛试题得到的新命题，从统一的作图法可以看出，命题1的结论完全可以推广到二次曲线，对于椭圆、双曲线、抛物线都成立。

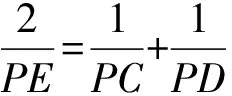
5 解题启示

射影几何作图不仅可以解决欧式几何的作图问题，还能将问题由圆推广到二次曲线，充分揭示圆与二次曲线的内在关系，从宏观角度给出问题的本质属性。但射影几何也不是万能的，只是通过讨论几何图形的位置来给出相应结果[7-10]。