高等数学教学效果优化策略研究

佟珊珊，陈 森，路 宽

(1.陕西师范大学 数学与统计学院，西安 710119；2.西北工业大学 力学与土木建筑学院，西安 710072)

1 高等数学教学存在的问题

1.1 学生对高等数学认知不足

与初等数学相比，高等数学具有更高的抽象性、概括性。高等数学开设在大学一年级课程中，学生很难理解高等数学中的抽象表述并灵活运用，例如极限的“ε-δ”语言等知识。在课堂教学中，教师通常更注重知识的传递，理论证明往往占用大部分课堂时间。但学生对理论证明的兴趣不高、关注度不够，难以真正理解定义及定理所蕴含的数学真理，只能死记硬背概念或结论，不能活学活用，这在一定程度上挫伤了学生学习高等数学的积极性。

1.2 传统教学方式存在局限性

部分教师为了追求教学内容的严谨性，强化核心知识的讲解，主要采用传统的教学方法。传统教学方式以教师讲解为主，教师与学生课上互动较少，学生参与感不足。对于较为复杂的定理证明，学生很难跟上教师的讲授思路。教师与学生课下交流不足，不能及时了解学生对知识的理解和运用情况。此外，在高等数学教学过程中，教师忽视在教学中融入趣味性元素，难以激发学生的学习热情。

1.3 缺乏数学实际应用的探究

高等数学具有高度的抽象性，学生不了解高等数学知识在实际问题中发挥的作用。“用”的概念不强，“学”的动力不足。教师注重对学生计算能力的锻炼，但在一定程度上忽视了应用能力的培养。传统的考核制度侧重于利用公式直接计算，而对利用所学知识解决物理、经济、工程等实际问题的能力考核评价较少，导致学生不够重视对高等数学实际应用能力的训练。

2 高等数学教学效果优化策略

2.1 融入数学史的学习

数学史是研究数学发展和规律的一门学科，它不仅追溯数学史料，而且蕴含着深刻的数学思想。在高等数学授课过程中融入数学史，适当介绍数学家的轶事、数学定理证明的发展历史等，能够活跃课堂气氛，增强学生学习数学的兴趣。通过学习数学史，也能让学生认识到数学来源于生活，是认识世界的重要工具。此外，通过了解数学家的生平，学生能够学习数学家们在追求数学真理过程中展现出的优秀品质，有助于培养学生的数学素养。

教师可以在讲授定义、定理前，通过相关的数学问题、数学家轶事作为引言，将数学史融入到教学中[1]。例如，在讲授极限的概念时，可以借助经典问题吸引学生的关注，提高教学效果。如《庄子·天下篇》中的“一尺之棰，日取其半，万世不竭”。意思是一尺长的木棍，每天截取它的一半，把每次截取的长度排成数列，无限制地进行下去，当天数无限增加趋于正无穷时，截掉的长度就无限接近于零，则零就是这个数列的极限。这个故事生动形象地描述了极限的概念，便于学生理解和掌握数学问题。

2.2 结合问题驱动教学模式

问题驱动教学模式是以问题为导向的教学方法，通过设立一系列环环相扣的问题，激发学生的探索热情，引导学生在主动分析问题、解决问题的过程中学习新知识。高等数学中许多概念、定理的得出都是受问题驱动而展开的猜想、假设、推理和验证。因此，在高等数学教学过程中适当采用问题驱动的教学模式有利于提高学生的学习热情和学习动力，培养学生自主学习，善于探索和勇于实践的能力。

在教学过程中，教师可遵循抽象内容具体化、以旧知识带动新知识、联想类比等基本原则设立问题情境[2]。例如，在导数定义的教学活动中，要以学生为主体，教师为主导，知识为主线。以恰当的问题为纽带，给学生创设自主探究、合作交流的空间，指导学生类比探究形成导数概念，让学生在参与中获取知识，拓展思维。

以如下问题作为引言，即“同学们在乘坐高铁时，在高铁车厢前面可以看到一块显示高铁时时运行速度的电子显示屏，这样的瞬时速度该如何计算”。将这一问题转化为数学问题，如图1所示。

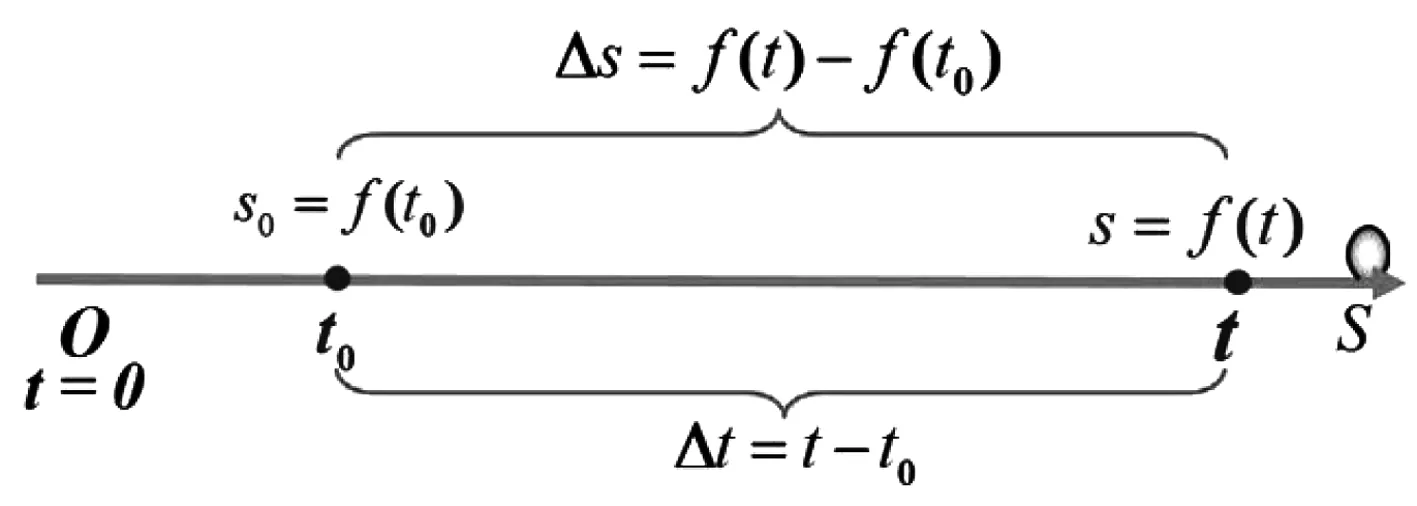
图1 瞬时速度计算

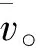
从平均速度循序渐进到瞬时速度，遵循知识的延续和迁移，从旧知识出发激发了学生的学习兴趣。通过实际问题巩固学生对导数物理意义的掌握，加深对知识的理解。

2.3 有效利用思维导图

思维导图是简单、高效表达发散性思维的工具，通过图文并重的方法将各级主题之间的相互联系清晰地展现出来[3]。学生能够掌握单一的知识点，但很难建立起各个章节之间知识点的联系，在解题过程中思维不够灵活和拓展。针对这一问题，教师在复习总结时，应运用知识思维导图建立各章节知识点框架，帮助学生建立一条能够贯穿各章节的知识线，完成知识点的衔接，提高学生对高等数学的综合认识，培养学生灵活运用知识点解决问题的能力。

以一元函数微分学为例，思维导图如图2所示。图2分层次展示了教材中一元函数微分学所包含的重要知识点，有助于学生系统地、综合地掌握各个知识点，提高学习效率。

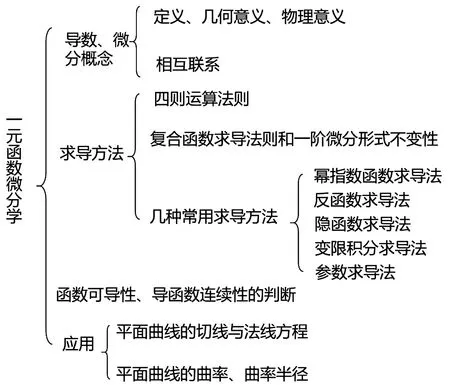
图2 一元函数微分学思维导图

2.4 注重理论与实际相结合

高等数学虽然抽象性较强，但其来源于实际问题，是对实际问题探索的成果。因此，在高等数学教学过程中，教师应重视抽象理论知识在实际问题中的应用，培养学生解决实际问题的能力，拓展学生的数学思维[4]。除了进行理论知识地讲授，教师可适当探讨其与实际生活的联系，介绍知识点在实际问题中的应用。例如，利用常微分方程建立传染病模型，对传染病的传播情况进行预测。SIS(Susceptible-Infective-Susceptible Model)模型是经典的传染病模型之一，该模型考虑感染者恢复后可能会出现反复感染的情况，如日常感冒、发烧等。设t时刻，S(t)为易感染者，I(t)为感染者，N(t)为总人口，β为传染率，r表示在单位时间内感染者接触到的易感者人数，γ表示感染者康复的概率，则SIS模型可表示为

初始条件S(0)=S0,I(0)=I0。通过求解方程，对传染病的传播行为进行预测，以指导对传染病的预防和控制，如通过建立华支睾吸虫病SIS模型，研究预防性化疗措施对疾病控制的长期效果[5]。将理论知识与实际应用相结合，一方面使学生认识到数学在实际生活中的应用性，激发学习数学知识的动力，另一方面能够拓展学生的数学思维，提升数学素养。

3 结语

在高等数学教学过程中，教师应充分认识到学科的重要性，培养学生的数学素养，为学生的专业发展夯实基础。在阐述高等数学教学现状的基础上，从引入数学史、问题驱动教学模式、利用思维导图及理论与实际相结合等方面探讨了优化高等数学教学效果的策略，有效提升了教学质量和教学效果。