由Grothendieck型刻画生成的非超弱紧测度和赋范半群

涂昆

(扬州大学 数学科学学院， 江苏 扬州 225002)

Banach空间X是自反的当且仅当其闭单位球BX是弱紧的.一致凸Banach空间是自反的，但是自反空间不一定是一致凸的[1].由James[2]和Enflo[3]的结论，可知Banach空间是一致凸当且仅当它是超自反空间.许多学者研究由空间的局部性质刻画超自反性[4-7]，文献[8-9] 引入超弱紧集的概念，并证明一个Banach空间是超自反的当且仅当其闭单位球是超弱紧集.弱紧集和自反空间的关系一样，超弱紧性质被视为超自反空间的局部化，因此，超弱紧集提供了一个研究超自反和一致凸性的新方向.

非紧性测度是抽象概念“紧性”的定量刻画，衡量Banach空间中的一个有界集离“紧”的差距.自1930年Kuratowski[10]引入集合非紧性测度以来，非紧性测度一直受到研究者的重视，并被推广成各种形式，在积分方程理论中得到广泛应用[11-14].本文研究由Grothendieck型刻画生成的非超弱紧测度和赋范半群.

1 基本概念

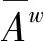
定义1称集合A⊂X为相对超弱紧集，如果对任意自由超滤子U，那么AU是相对弱紧集，相对超弱紧集的弱闭包是相对弱紧集.

容易看到，相对超弱紧集是有界的.Cheng等[9]证明相对超弱紧集在连续线性映射下的像是相对超弱紧集，并且如果A，B是相对超弱紧集，那么A∪B，A×B，A+B是相对超弱紧集.另外，相对超弱紧集A的凸包CO(A)也被证明是相对超弱紧集.

Cheng等[9]得到超弱紧集的Grothendieck型刻画定理，非空有界集A⊂X是相对超弱紧集当且仅当对任意正数ε>0，存在相对超弱紧集S⊂X，使得A⊂S+εBX.由此刻画定理，定义函数σ:β(X)→[0,∞)为

σ(A)=inf{t>0:A⊂S+tBX,S为相对超弱紧},∀A∈β(X).

容易证明σ具有如下7个性质：

1)σ(A)=0当且仅当A是相对超弱紧集；

2)σ(A)≤σ(B)，如果A⊂B；

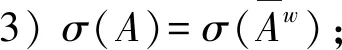
4)σ(A)=σ(CO(A))；

5)σ(A∪B)=max{σ(A),σ(B)}；

6)σ(A+B)≤σ(A)+σ(B)；

7)σ(tA)=|t|σ(A),t∈R.

2 主要定理及证明

设βC(X)和SC(X)分别表示X上的非空有界闭子集和非空超弱紧子集.在BC(X)上定义加法和数乘分别为

λ·A={λa:a∈A}，

则(βC(X),⊕,·)为模，同样，SC(X)是(βC(X),⊕,·)的一个子模.注意到模是一个半群.

考虑到商半群为βC(X)/SC(X),如果A∈βC(X)，那么

A+SC(X)∈βC(X)/SC(X).

记[A]=A+SC(X)，商半群中具有继承而来的加法和数乘，即任意[A],[B]∈βC(X)/SC(X)，λ∈F，[A]+[B]=[A+B],λ[A]=[λA],则βC(X)/SC(X)在上述加法和数乘下为模.进一步可以证明，非紧性测度σ可以生成此模上的一个范数.

定理1由‖·‖:βC(X)/SC(X)→[0,∞)，‖[A]‖=μ(A)定义的函数为半群βC(X)/SC(X)上的范数.

证明 1) 函数‖·‖是良定义的.若有A,B∈βC(X)，使得[A]=[B]，则存在相对超弱紧集S，使得A=B+S.进而‖[A]‖=σ(A)≤σ(B)+σ(S)=σ(B)=‖B‖.同理，由B⊂A-S,可得‖B‖≤‖A‖，故函数‖·‖是良定义的.

2) 若存在A∈βC(X)，使得‖[A]‖=0，则σ(A)=0，进而A是超弱紧集，即[A]=0.

3) 任意A,B∈βC(X)，‖[A]+[B]‖=σ(A+B)≤σ(A)+σ(B)=‖A‖+‖B‖.

4) 任意A∈βC(X)，λ∈R，‖t[A]‖=σ(tA)=|t|σ(A)=|t|‖[A]‖.

在β(X)上赋予Hausdorff度量dH，即任意A,B∈β(X)，有

则(βC(X),dH)为完备度量空间，(SC(X),dH)为其闭子空间.

设S(X)表示X中的非空相对超弱紧集构成的集族，则可得到关于σ的表示定理(定理2).

dH(A,S)<(β+ε),

进而σ(A)≤β+ε.由ε的任意性,可知σ(A)≤β.

另一方面，若存在相对超弱紧集S，使得

A⊂S+(σ(A)+ε)BX，

显然d(a,S)≤(σ(A)+ε).若存在s1∈S，使得d(A,s1)>(σ(A)+ε)，则

A⊂S{s1}+(σ(A)+ε)BX.

进而存在W⊂S，使得A⊂W+(σ(A)+ε)BX且对任意w∈W，d(A,w)≤(σ(A)+ε).因此，有dH(A,W)≤(σ(A)+ε)，即证.

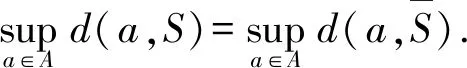
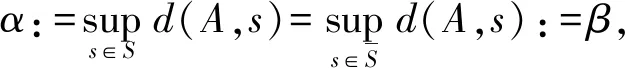
χ(A)=inf{‖A/Y‖:Y为有限维子空间}.

对于超弱紧集的情形，如定理3所示.

定理3设X为无穷维Banach空间，则对任意A∈β(X)，有

σ(A)≤inf{‖A/Y‖:Y为超自反子空间}.

证明 设Y为X的超自反子空间，‖QY(A)‖≠0，否则，A⊂Y为相对超弱紧集，则任取a∈A，n∈N，存在y∈Y，使得

‖a-y‖≤‖QY(a)‖+1/n，

进而‖y‖≤‖a‖+‖QY(a)‖+1/n.故存在有界集S⊂Y，使得A⊂S+(‖QY(A)‖+1/n)BX，由S为相对超弱紧及n的任意性，可知σ(A)≤‖QY(A)‖，即命题得证.

与紧集的情形不同，超弱紧生成空间是超弱紧算子生成，而不是超自反空间生成.任何一个紧集一定是某个有限维空间中的子集，与此不同的是， Raja[6]构造了一个Banach空间X，且存在一个超弱紧集S⊂X，但S不是任何超自反子空间的子集.故上述定理的逆并不一定成立.

设X，Y是Banach空间，如果T(BY)是超弱紧集，有界线性算子T:Y→X称为超弱紧算子.Astala[15]研究了一类由算子定义的测度，被视为连接算子理论与空间的桥梁，类似地，可以构建一个由超弱紧算子生成的关于此测度的一个子类.对任意A∈β(X)，定义

γ(A)=inf{t>0:A⊂T(BY)+tBX,T是超弱紧算子},

其下确界取遍所有Banach空间Y和超弱紧算子T.

定理4设X为Banach空间，任取A,B∈β(X)，有

1)γ(A)≤γ(B)，如果A⊂B；

2)γ(A)=γ(CO(A))；

3)γ(A∪B)=max{γ(A),γ(B)}；

4)γ(A+B)≤γ(A)+γ(B)‘

5)γ(tA)=|t|γ(A),t∈R.

定理5设X为Banach空间，任取A∈β(X)，则σ(A)=γ(A).

证明 当T是Y到X的超弱紧算子时，T(BY)是相对超弱紧集，故σ(A)≤γ(A).另一方面，由文献[5]，给定任一相对超弱紧集S，必存在一个自反空间Y及超弱紧算子T:Y→X，使得S⊂T(BY)，进而γ(A)≤σ(A)，命题得证.