预应力钢丝绳-聚合物砂浆面层抗弯加固持荷RC梁数值分析及承载力计算

柳战强, 叶勇, 郭子雄, 严东升, 苏文春

(1. 华侨大学 土木工程学院， 福建 厦门， 361021；2. 华侨大学 福建省结构工程与防灾重点实验室， 福建 厦门， 361021；3. 闽鑫建工集团有限公司， 福建 厦门， 361000)

随着城市基础结构及设施鉴定加固问题的日益凸显，各种新型加固技术应运而生.其中，钢绞线网片-聚合物砂浆面层加固技术作为一种新型加固技术，因具有耐久性好、施工简易、加固性能优越等特点，在加固领域中得到较充分的研究[1-7].现有研究表明，加固试件易发生界面剥离破坏，严重影响加固试件的力学性能[3-7].因此，柳战强等[5]提出一种新型预应力高强钢丝绳-聚合物砂浆面层(PSWR-PM)加固技术，该加固技术采用较大直径(如8 mm)的钢丝绳和新型锚固形式等方法，可解决加固需求大、粘结锚固需求高、加固界面易剥离等问题.该加固技术的要领是张拉钢绞线网/钢丝绳，并将其锚固在混凝土试件上，再通过聚合物砂浆面层使加固材料和混凝土试件成为整体共同受力；而端部锚固件只起到初期张拉和锚固钢丝绳/钢绞线网的作用，较少参与加固材料的荷载传递工作，保证了锚固的安全性.

在工程实践中，试件加固常需要在承受结构质量、施工荷载及一些不可移除的原有荷载等情况下进行[8-11]，加固材料与原试件间会产生应变滞后问题.解决加固材料应变滞后问题是研究加固持荷结构力学性能的关键.然而，针对钢绞线网片/钢丝绳-聚合物砂浆加固持荷结构的力学性能研究尚不充分[12-14]，这在一定程度上制约着钢绞线网片/钢丝绳-聚合物砂浆技术的进一步推广.

本文基于预应力钢丝绳-聚合物砂浆面层(PSWR-PM)抗弯加固钢筋混凝土(RC)梁的试验模型，建立有限元模型，引入“生死单元”技术中的“*Model change”和“*Elcopy”命令，进行持荷加固RC梁的数值分析，研究不同持荷比对加固试件力学性能的影响；最后，基于平截面假定和钢丝绳滞后应变计算公式，提出持荷加固RC梁受弯承载力计算公式.

1 抗弯加固RC梁数值模拟

1.1 试验模型

以3根RC梁作试验模型，其中1根为未加固梁，2根为加固梁，主要试件参数如表1所示.表1中：ρr为配绳率；η为预应力水平.试件SB-1采用加固Ⅰ法，即梁底张拉钢丝绳并锚固，再分层抹压砂浆；试件SB-2采用加固Ⅱ法，即抹压第1层砂浆至钢丝绳形心位置，随后张拉钢丝绳，再抹压第2层砂浆.

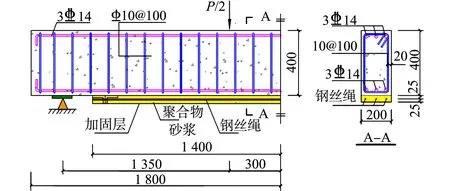
图1 试件尺寸及配筋形式(单位：mm)Fig.1 Dimension and reinforcement form of specimens (unit: mm)

表1 主要试件参数Tab.1 Main test parameters

试件尺寸及配筋形式，如图1所示.图1中：P为作动器施加的荷载.每根梁均采用3根直径为8 mm的6×19+IWS镀锌钢丝绳进行梁底加固，并对每根钢丝绳施加0.22的预应力水平，产生9.49 kN的拉力，其中，钢丝绳的合力点距梁底25 mm；随后，按照不同加固工艺，人工压抹厚50 mm的单组分聚合物砂浆.纵筋和箍筋分别为HRB400级和HPB300级；28 d混凝土及聚合物砂浆立方体试块的抗压强度分别为57.8，55.6 MPa；单根钢丝绳的有效面积为24 mm2，破断力为42.2 kN；各材料力学性能参见文献[5].试验采用跨中两点对称加载，纯弯段长度为600 mm.

1.2 有限元模型

以节1.1试验模型为研究对象建立有限元模型，其中，聚合物砂浆与混凝土均为脆性材料.为准确描述脆性材料进入塑性阶段后拉压屈服面的强化及软化特性，采用损伤塑性模型；普通钢筋采用理想弹塑性模型，不考虑钢筋屈服后的应变强化；钢丝绳材料采用线弹性本构模型，各材料属性均采用文献[5]的试验实测值.在模型建造过程中，采用降温法对钢丝绳施加预应力，钢丝绳材料热膨胀系数取1×10-5℃-1.为节约计算成本，加固层与RC梁间接触采用绑定约束，钢丝绳与砂浆间接触采用内嵌模式.

持荷RC梁的加固模拟主要解决加固层单元与变形后的混凝土梁间单元不协调变形等问题，即处理加固层单元在激活前后位置不同的难题.由于ABAQUS软件是在加固单元的原始位置激活单元，而实际结构受力分析时要求加固单元在变形后的位置上以无初始应变的方式激活单元.在“生死单元”法中引用“追踪单元”可很好地解决这一问题[15].具体实现方法如下.

1) 建立3个单元集合，即“钝化单元”、“非钝化单元”和“完全弹性单元”集合.其中,“完全弹性单元”即“追踪单元”，要求除节点编号外，该单元集合的单元数量、形状及类型与“钝化单元”完全一致，且共享节点，该要求可通过“*Elcopy”命令实现.该单元刚度很小，且质量无限小，它的存在不影响原有结构的计算结果.“钝化单元”集合为未激活单元，其钝化与激活可以通过“*Model change,remove,add”命令完成.

2) 先将RC梁和加固层(包括钢丝绳与聚合物砂浆层)分别定义为“非钝化单元”和“钝化单元”，同时，设置加固层的“追踪单元”.

3) 初始荷载下，“追踪单元”随“非钝化单元”一起变形，但“追踪单元”只变形，不参与RC梁受力.

4) 在负载状态下，将“钝化单元”激活，成为另一个“非钝化单元”，与原“非钝化单元”即变形后的RC梁绑定成为整体；随后，对激活后加固层内的钢丝绳施加预应力.

5) 加固完毕后，对新模型继续加载至目标荷载.

1.3 模型验证

通过荷载(P)-挠度(Δ)曲线及特征点的对比，验证有限元模型的正确性，对比结果如表2和图2所示.表2中：Fi,exp，Fi,num分别为相应试件的极限承载力的试验值和有限元模拟值；FCB,exp，FCB,num分别为

表2 试验结果与有限元模拟结果的对比Tab.2 Comparison between experimental and finite element simulation results

图2 荷载-挠度对比曲线Fig.2 Comparison of load-displacement curves

试件CB的极限承载力的试验值和有限元模拟值.图2中：Pu为理论承载力.

从对比结果可以看出：荷载-挠度曲线相近，极限承载力相差在6%以内，有限元模拟结果与试验结果吻合良好;各试件开裂前，加固试件的荷载-挠度曲线均高于未加固试件CB;与未加固试件CB相比，加固试件的屈服荷载、极限承载力均有明显提高;试件SB-1的破坏形态为剥离破坏形态，会影响加固试件的延性系数，但对荷载-滑移曲线、极限承载力的影响较小;发生弯曲破坏的试件SB-2，其承载力和延性比均略优于发生界面剥离破坏的试件SB-1，但其极限挠度却略小于试件SB-1.

试件SB-1，SB-2的荷载-滑移曲线和极限承载力模拟结果与试验结果相当，误差仅为1%(表2)；而试件SB-1的数值模拟破坏形态与试验结果存在差别，分析原因是为了提高运算效率，有限元模型中加固层与RC梁之间的接触、钢丝绳与砂浆之间的接触分别采用绑定约束和内嵌模式，未体现砂浆层界面剥离破坏和钢丝绳脱粘现象.综上分析认为，文中建立的有限元模型是可靠的，其分析方法和有限元模型可用于以弯曲破坏为主的抗弯加固持荷RC梁的模拟分析.

2 持荷加固RC梁模拟结果及分析

2.1 持荷30%的加固试件数值分析

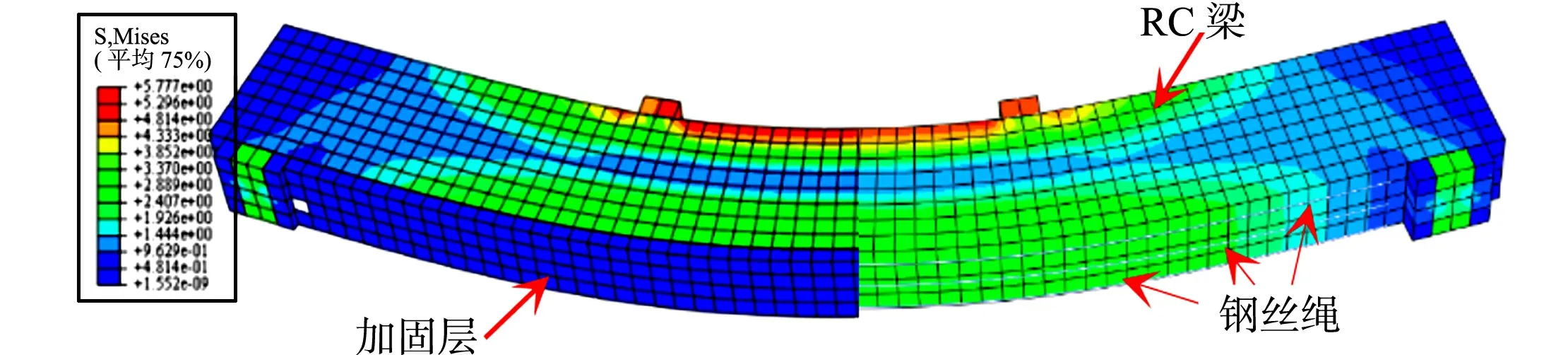
(a) 预加载阶段

(b) 加固层激活并施加预应力阶段 (c) 加固试件共同受力阶段 图3 持荷试件B4在不同受力阶段的受力云图Fig.3 Stress nephogram of preloaded specimen B4 in different loading stages

在节1.2数值模型的基础上，对有限元分析方法进行修改，模型的数据和参数均未改变.以试件SB-2的有限元模型为基础模型，引入“钝化单元”、“非钝化单元”和“跟踪单元”集合.加载过程中，首先对未加固RC梁进行预加载模拟，分别加载至其承载力的10%～50%;随后在不卸载情况下，进行加固模拟，继续加载至破坏.

持荷试件B4在不同受力阶段的受力云图，如图3所示.试件B4是未加固RC梁先加载至其承载力的30%后，再完成加固的.钢丝绳和受拉钢筋在受力全过程中的力学性能，如图4所示.图4中：σw，εw分别为钢丝绳的应力、应变；εs为受拉钢筋应变.

(a) 试件B4的荷载-挠度曲线

(b) 持荷下钢丝绳的应力-应变关系 (c) 各材料的荷载-应变关系图4 试件挠度及材料应变随荷载变化规律Fig.4 Variety of deflection and material strain with load

由图3,4可知：在加固单元(SW-PM加固层)激活前，试件B4与未加固试件CB的荷载-挠度曲线重合；试件B4的混凝土梁出现应力，而聚合物砂浆层及钢丝绳未出现明显的应力，说明加固单元随RC梁一起变形，但未参与受力(图3(a))；随后，加固层单元被激活，并对钢丝绳施加0.22的预应力水平(每根钢丝绳产生9.49 kN的拉力)，此时,荷载-挠度曲线及钢丝绳材料应力-应变曲线(图4)出现拐点，之后试件的挠度减小，刚度提升，说明加固层单元被成功激活，并参与RC梁共同受力；同时，试件B4的受压边缘和受拉边缘的混凝土应力降低，说明加固层承担了一部分外荷载，钢丝绳的预应力使RC梁出现预压拱形态[16-17](图3(b)).

在钝化阶段，钢丝绳只参与RC梁变形，不参与受力，所以在应力-应变曲线上表现为应变增长，而应力增长较小.在激活阶段，聚合物砂浆层与钢丝绳均被激活，并完成预应力施加，所以，在钢丝绳的应力-应变曲线上出现拐点.之后，加固层与RC梁共同受力，承担外荷载，降低原RC梁中材料的应力，所以，在钢筋荷载-应变曲线上也出现较小幅度的拐点.这些现象说明加固层单元被成功激活，在“生死单元”技术中利用“*Model change”和“*Elcopy”命令可有效完成负载条件下加固RC梁的有限元模拟.

2.2 不同持荷水平下的抗弯加固梁数值分析

不同持荷比下加固试件的荷载-挠度曲线和极限承载力，如图5所示.图5中：Fpre/FCB，num为持荷比，Fpre为加固前对RC梁的预加荷载；Fi,num/FCB,num表示承载力的提升幅度.

(a) 荷载-挠度曲线 (b) 预加载对极限承载力影响曲线图5 不同持荷比下加固试件荷载-挠度曲线和极限承载力变化Fig.5 Load-deflection curves and ultimate bearing capacity variations of strengthened members under different preload ratios

由图5(a)可知：预加载阶段，各加固试件的刚度与未加固梁CB初始刚度重合；随后，荷载-挠度曲线出现拐点，这是因为加固层单元被激活，使加固试件挠度减小，刚度瞬间提高；之后，加固层与RC梁成为整体共同受力变形.

由图5(b)可知：随着预加载程度的提高，加固梁的极限承载力提高的幅度逐渐降低，其初始刚度也不断降低；当RC梁在10%～50%的不同预加载条件下进行加固时，其极限承载力相对一次受力下降4%～13%；当预加载小于未加固梁极限荷载的20%时，加固试件的极限承载力与完好加固梁的承载力相当，其降低程度在5.2%以内，RC梁损伤较小，可按一次受力情况考虑；当预加载高于加固梁极限荷载的20%时，加固试件的极限承载力降低程度超过5%，设计时需考虑因预加载产生的加固材料滞后应变对加固试件承载力的影响.

试件极限承载力模拟值与计算值的对比，如表3所示.表3中：FSB-2,num为试件SB-2极限承载力的有限元模拟值；部分数据(试件DBW0，SW1，SW3)为文献[13]的试验结果.

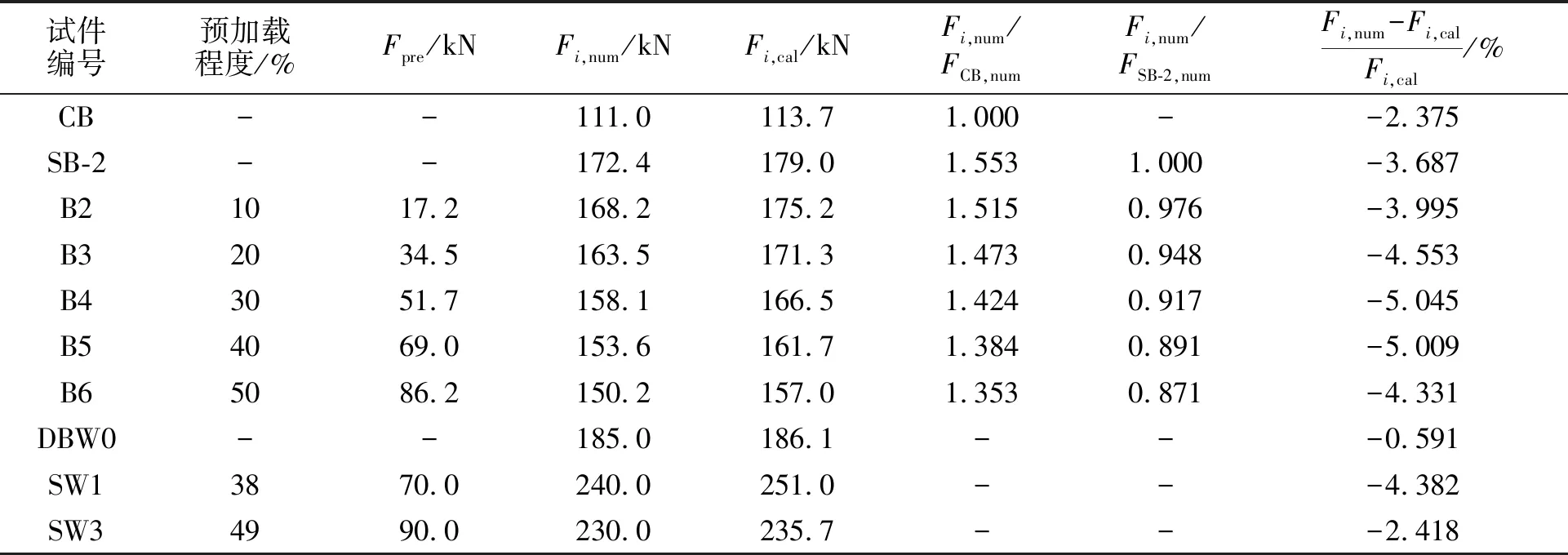
表3 试件极限承载力模拟值与计算值的对比Tab.3 Comparison of simulated and calculated ultimate capacity of specimens

3 受弯加固持荷RC梁极限承载力计算

3.1 基本假定

RC梁在承受一定的初始荷载下进行加固，加固层与原试件间存在应力-应变滞后现象，解决加固层应变滞后值问题是进行负载条件下加固梁抗弯承载力计算的关键步骤.

现作以下假定：1) 加固梁横截面应变沿梁高呈线性分布，符合平截面假定；2) 在整个受力过程中，各种材料变形协调,其中，聚合物砂浆层与原混凝土间界面、钢丝绳与聚合物砂浆层间及受力钢筋与混凝土间粘结可靠，无滑移剥离等现象出现；3) 忽略受拉区混凝土和聚合物砂浆的作用，受拉区的拉力全部由钢筋和钢丝绳承担；4) 混凝土的应力-应变关系采用Hognestad建议的模型[18],钢筋的应力-应变关系采用理想弹塑性模型,钢丝绳假定为线弹性材料，应力-应变本构关系为σw=Ewεw，其中，Ew为钢丝绳的弹性模量.

3.2 加固梁滞后应变计算

图6 滞后应变计算简图Fig.6 Calculation diagram of lagged stain

在初始弯矩M0作用下，加固梁的滞后应变可按图6计算简图进行计算.图6中：h为梁高;h0为截面有效高度;εs0为初始荷载作用下的钢筋应变;εc0为混凝土受压区边缘的压应变;xc0为混凝土受压区的高度;Cc0，yc0分别为受压区混凝土合力和作用点位置;σy为初始荷载作用下的受拉钢筋应力；As为受拉钢筋面积.基于平截面假定，得到受拉钢筋应变，以及距受压区混凝土边缘y处的压应变εc，y为

(1)

(2)

在初始弯矩M0作用下，受压区混凝土压应力的合力分两种情况计算.

1) 当0<εc0<ε0时，Cc0和yc0分别为

(3)

2) 当ε0<εc0<εcu时，Cc0和yc0分别为

(4)

式(3)，(4)中：σc，y(εc，y)为混凝土压应变εc，y时的应力，按Hognestad建议的模型[18]选取；b为混凝土梁的宽度;fc为峰值应力，取棱柱体极限抗压强度；ε0为相应于峰值应力的应变，取0.002；εcu为极限压应变，取0.003 8.

根据截面受力平衡条件，可得

Cc0=Ts0.

(5)

式(5)中：Ts0为受拉区钢筋的合力.

对纵向受拉钢筋合力点取矩，可得

M0=Cc0(h0-yc0).

(6)

根据平截面假定，得到在初始弯矩M0作用下受拉钢丝绳滞后应变εw0为

(7)

式(7)中：δ为加固层厚度.

3.3 加固梁受弯承载力计算

预应力钢丝绳-聚合物砂浆加固RC梁极限承载力的极限状态，主要考虑两种破坏形态：1) 受拉钢筋屈服，混凝土压溃时钢丝绳拉断；2) 受拉钢筋屈服，混凝土压溃时钢丝绳未被拉断.文中有限元模拟及理论承载力公式推导均以加固试件发生钢丝绳拉断的破坏形式为依据.

加固试件极限承载力计算简图，如图7所示.图7中：Mu为极限弯矩；xc为极限荷载状态下混凝土梁受压区高度;as和as′分别为混凝土梁受拉区和受压区保护层厚度;Aw,As′分别为钢丝绳和受压钢筋的面积；εw,load为外荷载作用下钢丝绳应变；εcu0为混凝土受压区边缘的压应变；xcu0为极限状态下受压区高度；Ccu，yc分别为极限状态下受压混凝土合力及作用点位置；fy′，fy分别为受压钢筋和受拉钢筋的屈服强度；ψw定义钢丝绳的强度发挥系数.

图7 加固试件极限承载力计算简图Fig.7 Calculation diagram of ultimate bearing capacity of strengthened members

根据平截面假定可得到截面应变关系为

(8)

ψw为加固梁受弯破坏时钢丝绳发挥的应变与其极限拉应变的比值，其表达式为

(9)

式(9)中：ψw≤1.0，当计算值ψw>1.0时，取ψw=1.0；εw,pre为由预拉力产生的钢丝绳初始应变；εwu为钢丝绳的极限拉应变.

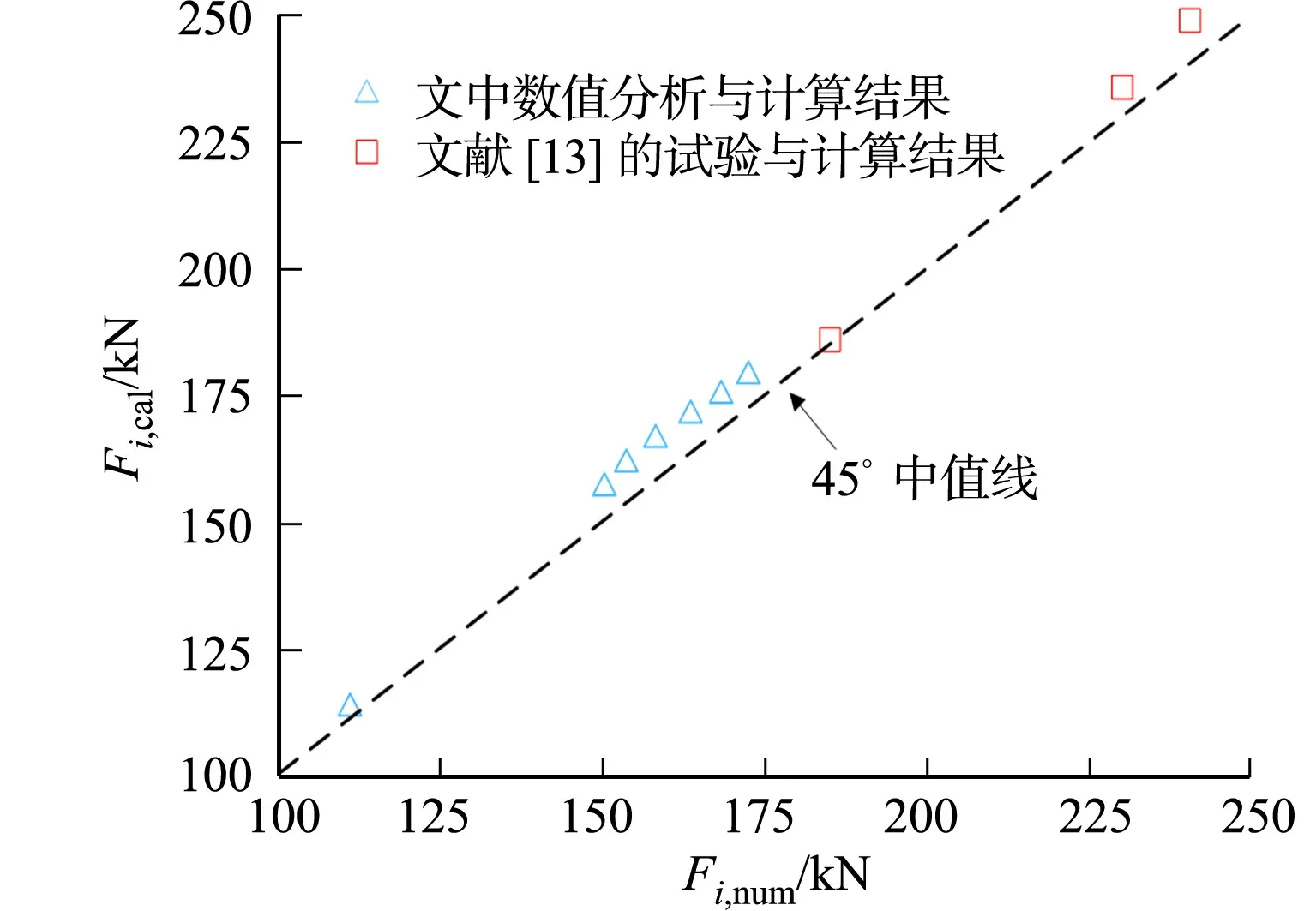
图8 模拟结果与计算结果的对比Fig.8 Comparison between simulation results and calculation results

根据截面受力平衡条件，可得

(10)

对钢丝绳合力点取矩，可得

(11)

加固梁极限承载力模拟结果与计算结果的对比，如图8和表3所示.图8中：Fi,cal为相应试件的极限承载力计算值.

由表3可知：计算结果与试验结果、模拟结果吻合较好，误差在10%以内，证明所推导公式的有效性.

4 结论

建立预应力钢丝绳-聚合物砂浆面层抗弯加固持荷RC梁的有限元分析模型，进行不同持荷比下加固梁的力学性能分析，并提出加固梁的极限承载力计算公式.在所研究的参数范围内，可以得到以下3个重要结论.

1) 在“生死单元”技术中，利用“*Model change”和“*Elcopy”命令，可以较好地解决持荷条件下加固层与RC梁之间单元不协调变形等问题，有效完成持荷条件下加固RC梁的数值计算分析.

2) 当RC梁在10%～50%的不同预加载条件下进行加固时，其极限承载力相对一次受力下降了4%～13%;当预加载小于未加固梁极限承载力的20%时，混凝土损伤较小，试件可按一次受力情况考虑；当预加载高于未加固梁极限承载力的20%时，加固材料滞后应变不可以忽略，需考虑加固材料滞后应变对极限承载力的影响.

3) 提出负载条件下钢丝绳滞后应变计算公式及持荷加固RC梁的极限承载力计算公式，计算结果与试验值及模拟结果吻合良好.