模糊β-最小和最大描述的矩阵表示

黄建新, 许丽婷, 于佩秋, 李进金,

(1. 华侨大学 数学科学学院， 福建 泉州 362021; 2. 闽南师范大学 数学与统计学院， 福建 漳州 363000)

Zakowski[1]在20世纪80年代提出的覆盖粗糙集理论是Pawlak经典粗糙集理论[2]的推广，是知识发现、规则获取领域强有力的数学工具.它不仅丰富了粗糙集理论，而且扩展了粗糙集理论在实际问题中的应用.覆盖粗糙集和经典粗糙集都旨在处理定性(离散)数据，由于数据库中属性的值既可以是符号的，也可以是实值的[3]，因此，在处理实值数据集时存在很大的局限性.然而，模糊集理论[4]对于克服这些局限性非常有用，因为它可以有效地处理模糊的概念和分级的不可分辨性.因此，学者们将覆盖粗糙集模型扩展为模糊覆盖粗糙集.

许多学者基于模糊覆盖概念构建一些模糊粗糙集模型[5-8]，可以看作是覆盖粗糙集理论和模糊粗糙集理论的桥梁.在文献[5,7]中模糊覆盖的定义中β的值为1，具有一定局限性.Ma[9]通过引入模糊β-覆盖和模糊β-邻域的概念，定义更一般的模糊覆盖粗糙集模型，其中，参数β的范围为(0,1].Yang等[10]对模糊β-覆盖近似空间的性质和基于模糊覆盖的粗糙集模型[9]进行研究，提出3种基于模糊覆盖的粗糙集模型作为模型的推广.D′err等[11]将4种基于覆盖的邻域算子的定义扩展到模糊集，并且将模糊邻域算子与模糊覆盖相结合，得到16个不同的模糊邻域算子，并研究这16个算子之间的偏序关系.Yang等[12]通过引入邻域系统、模糊β-最小和最大描述等概念，研究这些模糊邻域算子的性质及其相互关系，并构造6种类型的模糊β-覆盖.

知识约简是知识发现的重要过程，是寻找最简单规则和最大泛化规则的重要手段，因而也是粗糙集理论的核心内容之一.知识库中知识并不是同等重要的，甚至其中某些知识是冗余的，当知识库数据是随机采集时，其冗余性更为普遍.冗余知识的存在一方面是资源的浪费(需要储存空间)；另一方面，干扰人们作出正确而简洁的决策.因此，知识约简的概念被提出，即在保持知识库分类能力不变的前提下，删除不相关或不重要的知识.通过知识约简，去掉不必要的知识，简化知识的同时，又不丢失基本信息.

在覆盖粗造集中，Wang等[13]提出IN-可约元及IN-约简，使用矩阵方法计算最小和最大描述和覆盖约简.在模糊β-覆盖近似空间中，Yang等[10]提出如果模糊β-覆盖中的某一个元素可表示为其余某些元素的并集，则这个元素被称为模糊β-覆盖中的可约元的定义.Yang等[14]提出了模糊β-最小描述的定义，研究模糊β-最小描述的矩阵表示，并讨论了模糊β-最小描述与约简之间的联系.但是在模糊β-覆盖中对于交可约元及模糊β-最大描述与约简之间的联系没有相关研究.因此，本文利用一种新的矩阵方法计算模糊β最小和最大描述，从而讨论模糊β-最大描述与约简之间的联系.

1 预备知识

实际上，文献[5,7]中的模糊β-覆盖的β=1是模糊β-覆盖的特例.

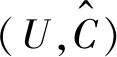
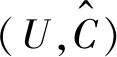
为了简化模糊β-最小和最大描述的定义，Yang等[12]给出x的β-邻域系统的定义.

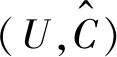
根据定义4，x∈U的模糊β-最小和最大描述分别表示为

2 模糊β-最小和最大描述与约简

2.1 矩阵表示

Yang等[14]提出模糊β-最小描述的定义通过，研究模糊β-最小描述的矩阵表示.通过定义一些新的矩阵，从而给出一种新的模糊β-最小和最大描述的矩阵表示.

根据定义5,有

对于β=0.5时，根据定义7,有

根据定义6，9，可以得到模糊β-最小描述的矩阵表示.

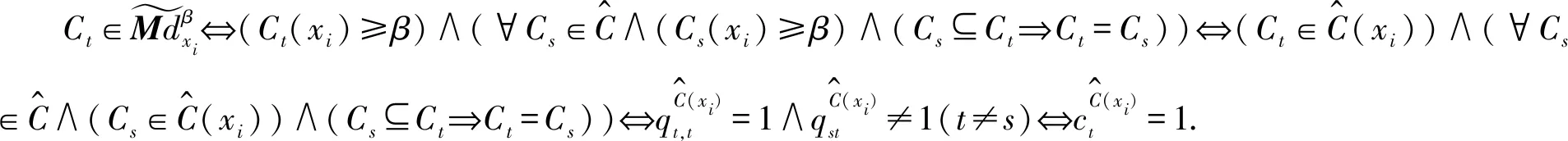
根据定义6,10，可以得到模糊β-最大描述的矩阵表示.

证明：类似定理1可证明.

提出的模糊β-最小和最大描述的矩阵表示跟文献[14]中的相比，计算步骤、利用到的矩阵较少.计算的方法简洁明了且快速，提高计算效率.

根据定义5,可得

对于β=0.5时，根据定义7,有

根据定义9，10，x1的模糊β-最小和最大描述的矩阵表示为

由上述步骤，x2,x3,x4,x5的模糊β-最小和最大描述的矩阵分别表示为

由定理1，当β=0.5时,模糊β-最小描述分别为

根据定理2，当β=0.5时,模糊β-最大描述分别为

2.2 模糊β-覆盖的约简

若模糊β-覆盖中的某一个元素可以表示为其余某些元素的并集，则这个元素被称为模糊β-覆盖中的可约元[10].模糊β-覆盖中的某一个元素可以表示为其余某些元素的交集的情况，即定义11.

定理4表明在模糊β-覆盖中删除交可约元不会生成任何新的交可约元，也不会使其他在原始模糊β-覆盖中的交可约元成为新模糊β-覆盖中的交不可约元.因此，可以通过同时删除所有交可约元或逐步删除可约元计算模糊β-覆盖的约简.

算法1计算模糊β-覆盖的约简

1： For i=1→n

2： C(xi)←0

3： For j=1→m

4： C(xi)←C(xi)∨Cj(xi)

5： End For

6： If C(xi)<β

β-覆盖”

8： Break

9： End If

10： End For

12： For k=1→m，

13： T←∅

14： For l=1→m

15： If Ck⊆Cl(k≠l)

16： T←T∩Cl

17： End If

18： End For

19： If T=Ck

21：End If

22：End For

2.3 模糊β-最大描述与约简的关系

Yang等[14]研究讨论模糊β-最小描述与去除并可约元的约简之间的联系.定理5研究模糊β-覆盖中去除交可约元的约简与模糊β-最大描述之间的关系.

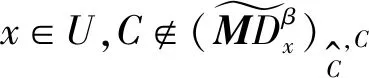
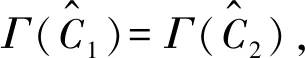
3 结束语

模糊β-覆盖近似空间是模糊覆盖的推广，可以解决模糊覆盖的局限性.模糊β-覆盖近似空间是近年才提出的定义，对其研究具有一定意义.在模糊β-覆盖近似空间中，许多基本问题与模糊β-最小和最大描述有关.对于具有大基数的模糊β-覆盖近似空间，使用集合表示解决关于模糊β-最小和最大描述的问题将是繁琐而复杂的.因此，有必要通过矩阵表示，将计算变为算法，并由计算机轻松实现.