知识基的布尔矩阵求解方法

谢小贤, 李进金, 陈东晓, 林荣德

(1. 华侨大学 数学科学学院, 福建 泉州 362021；2. 华侨大学 计算科学福建省高校重点实验室, 福建 泉州 362021；3. 闽南师范大学 数学与统计学院, 福建 漳州 363000)

知识空间理论(KST)是美国数学心理学家Doignon等[1]提出的，通过分析学生对不同水平的一系列有关问题的解答情况，获得学生的认知水平和学习路径，进而指导学生学习和教师教学，为教育教学提供有效的评价方法.Koppen等[2]用专家问询系统生成知识空间;Albert等[3]用问题系统构建知识空间;Dowling[4]在有限知识空间中提出一种构建知识基的方法；Falmagne等[5]对Dowling生成知识空间的算法进行改进，提高了效率.KST作为自适应教学和测试系统中最有效的知识表示理论[6-7]，已应用到教育领域中，例如，计算机知识诊断系统ALEKS[8]的开发与应用.文献[9-10]用知识空间理论分析学习路径等问题，并应用于化学教学.

形式概念分析(FCA)是德国数学家Wille[11]提出的，刻画对象与属性之间的概念层次结构，以及概念之间的泛化和特化关系，主要研究属性约简[12-20]、粒约简[21-22]、概念约简[23-25]和规则提取[13-14]等，作为一种有力的数据分析工具，已广泛应用于机器学习、知识评价等领域.Rusch等[26]建立了知识空间与形式背景之间的联系；Spoto等[27]将KST与FCA相结合，分析知识结构的有效性；李进金等[28]分析知识空间和形式概念分析之间的联系，以及知识基和知识空间的构建方法.

知识基是知识空间的核心,是知识空间的最小生成组，蕴含了知识空间的所有信息.因此，研究知识基具有非常重要的意义.由于知识空间与形式背景关系密切，而形式背景可看作一个布尔关系矩阵，可用矩阵方法解决形式背景中的属性约简[17-20]和概念约简[24-25]等问题.因此，本文将用矩阵方法研究知识空间中的原子和知识基.首先，通过KST和FCA的联系，导出反知识背景和知识背景；其次，利用布尔矩阵运算，研究(反)知识背景的关系矩阵、对象关系矩阵及其相关性质;最后，从知识状态、算子、布尔向量和布尔矩阵等角度，讨论知识空间中原子和知识基的特征，并给出求解方法.

1 预备知识

1.1 知识空间

设qi(1≤i≤m)表示问题，则称Q={q1,q2,…,qm}为所讨论知识的问题域.文中只考虑论域Q有限的情形.

定义1[1]学生在理想条件下能正确回答问题域Q中的问题所构成的集合称为知识状态，记为K.

定义2[2]设Q为问题域，K是Q的知识状态集族，并且K至少包含了空集∅和全集Q，称(Q,K)为知识结构，记

K={∅,K1,K2,…,Q}，

其中，每一个Ki⊆Q.

对知识结构(Q,K)，若K对有限并封闭，即

∀Ki,Kj∈K⟹Ki∪Kj∈K,

则称(Q,K)为知识空间，或称K为知识空间.

当Q有限时，称知识结构(Q,K)是有限的.当K有限时，称知识结构(Q,K)是实质有限的.

定义3[5]若G′包含G中所有有限个元素的并组成的集合，则称集族G′是G的张成，记为S(G)=G′，或称G张成G′.

由S(G)的定义可知，S(G)是并封闭的.

定义4[5]设集族F是并封闭的，若B是张成F的最小子集族，且B中的任何一个集合K，均不能由B中其他集合的并集表示，则称B为F的基，即S(B)=F.

定义4中最小子集族是指对于任意H⊆B且S(H)=F，有H=B.称知识空间的基为知识基，并约定∅∉B.另外，对知识空间(Q,K)，文中仅讨论Ki=Kj⟹i=j(Ki,Kj∈K)的情形.

引理1[5]任何实质有限的知识空间有知识基.

知识基B可生成唯一的知识空间(Q,K)，知识空间(Q,K)可确定唯一的知识基B，两者一一对应.

1.2 形式概念分析

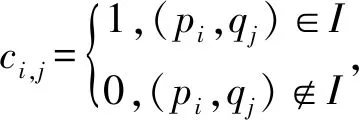
设X⊆P，B⊆Q，形式背景(P,Q,I)上的算子：X*={q∈Q|∀p∈X,pIq}，B*={p∈P|∀q∈B,pIq}，若满足X*=B,B*=X，则称(X,B)为形式背景(P,Q,I)上的一个形式概念(简称概念)，称X为概念的外延，B为概念的内涵.所有的概念构成的集合叫概念格，记为L(P,Q,I).一般地，对p∈P，q∈Q，记{p}*=p*，{q}*=q*.

若(X1,B1)和(X2,B2)是概念，其上的偏序关系定义为(X1,B1)≤(X2,B2)⟺X1⊆X2(B1⊇B2).定义下确界为(X1,B1)∧(X2,B2)=(X1∩X2,(B1∪B2)**)，上确界为(X1,B1)∨(X2,B2)=((X1∪X2)**,B1∩B2)，二者也是概念，从而L(P,Q,I)是完备格，称为(P,Q,I)的概念格.

1.3 知识空间与形式背景的联系

文献[26]建立了知识空间与形式背景的联系，由知识空间(Q,K)可构造出对应的反知识背景(P,Q,Ic)和知识背景(P,Q,I).

定义6[26]设有限集P={p1,p2,…,pn}，其中,pi(1≤i≤n)是被测试的对象，Q是问题集，I是P和Q之间的二元关系，pIq表示对象p不能解决问题q，称三元组(P,Q,I)是知识背景.

定义7[26]设有限集P={p1,p2,…,pn}，其中,pi(1≤i≤n)是被测试的对象，Q是问题集，Ic是P和Q之间的二元关系，pIcq表示对象p能解决问题q，则称三元组(P,Q,Ic)是相对于(P,Q,I)的反知识背景.

由知识空间(Q,K)构造知识背景(P,Q,I)的过程如下.

设K={K1,K2,…,Kn}，其中,K1=∅，Kn=Q，Ki(1≤i≤n)表示对象pi对应的知识状态，由此就将知识空间中的每一个状态和被测试的对象之间建立一一对应关系.于是有引理2.

引理2[26]知识背景(P,Q,I)与形式背景(K,Q,∉)是同构的,其中，K是知识状态集族，Q是问题集，∉是K×Q上的二元关系，表示某个问题q∉K，其中，q∈Q,K∈K.

设知识背景为(P,Q,I)，且X⊆P,B⊆Q,算子X*={q∈Q|∀p∈X,pIq}，B*={p∈P|∀q∈B,pIq}，若X*=B并且B*=X，则称二元组(X,B)是一个知识概念，简称概念，X是概念的外延，B是概念的内涵.

1.4 布尔矩阵的运算规律

定义在B0={0,1}上的向量称为布尔向量，记n维布尔行向量为Vn，记n维布尔列向量为Vn.通常把分量全为0的向量(0,0,…,0)或(0,0,…,0)T记作0，称为布尔零向量(简称零向量);否则,称为布尔非零向量(简称非零向量).记m×n阶布尔矩阵为Bm×n.

设α=(x1,x2,…,xn),β=(y1,y2,…,yn)∈Vn，则定义两个运算“ + ”与“ · ”为：1)α+β=(x1+y1,x2+y2,…,xn+yn)；2)α·β=(x1·y1,x2·y2,…,xn·yn)，其中，“ + ”表示取最大值，“ · ”表示数量乘积，取最小值.

对于行向量α和β，对于i∈{1,2,…,n}，若xi=1⟹yi=1，则记α≤β.如果α≤β且α≠β， 则记α<β.列向量相关内容可类似定义[29].

定义8[29]设子空间W⊆Vn，W的一个无关的子集合V称为W的一个基,当且仅当W=〈V〉(向量集合V的生成空间).

设A∈Bm×n.BR(A)表示由A的所有行构成的集合生成的空间R(A)的唯一基底,称为A的行基底,其基数称为A的行秩,用ρR(A)表示.类似地,BC(A)表示由A的所有列构成的集合生成的空间C(A)的唯一基底,称为A的列基底,其基数称为A的列秩,用ρC(A)表示[29].

设A=(ai,j)m×n,B=(bi,j)m×n,C=(ci,j)n×l为布尔矩阵，用AT表示矩阵A的转置.规定矩阵运算律如下：

1)A≤B当且仅当ai,j≤bi,j,i=1,2,…,m；j=1,2,…,n；

2)A∨B=(ai,j∨bi,j)m×n；

3)A∧B=(ai,j∧bi,j)m×n；

4)A-B=(ai,j∧(1-bi,j))m×n；

5) ～A=(1-ai,j)m×n；

6)A·C=(di,j)m×l，其中,di,j=∨1≤k≤n(ai,k∧ck,j)，∨表示取最大值，∧表示取最小值，则称A·C是布尔矩阵A与C的乘积[29].

2 原子的特征和知识基

知识基是知识空间的核心，是知识空间的最小生成组，可生成知识空间，而且知识基还能反应学生掌握的最基本的问题集族，为刻画知识空间和寻找学习路径提供依据.文献[4,5，28]对此作了一些研究.下面从知识状态、算子、布尔向量和布尔矩阵等角度讨论原子的特征和知识基.

2.1 基于知识状态的原子特征和知识基

定义10[4]设(Q,K)为知识空间，设F是问题域Q的非空子集族，q∈∪F,F中包含q的最小集合,称为元素q的一个原子.

引理4[4]如果知识空间(Q,K)的知识基B存在，则B可由所有的原子组成的集族构成.

因此，寻找知识基的过程就是找出知识空间的所有问题的原子.

定理1[5]设(Q,K)为知识空间，设F是问题域Q的任意非空子集族，知识状态K∈F是一个原子,当且仅当K∈F,其中,K=∪F∈FF.

推论1设(Q,K)为知识空间，设F是问题域Q的非空子集族，若对知识状态K∈K，满足K=∪F∈FF，则F⊆K.

推论2设(Q,K)为知识空间，则知识状态K∈K是一个原子,当且仅当K≠∪∅≠F⊂KF.

证明:充分性.若K∈K是一个原子，设K=∪∅≠F⊂KF.则对任意q∈K，必存在Fq≠∅，使q∈Fq⊂K，则K不是q∈K的原子，与条件矛盾，则K≠∪∅≠F⊂KF.

必要性.若K≠∪∅≠F⊂KF.取F={F|∅≠F⊂K}∪{K},则仅当K∈F时,有K=∪F∈FF，由定理1得知识状态K∈K是一个原子.

推论3设(Q,K)为知识空间，则知识状态K∈K不是一个原子,当且仅当K=∪∅≠F⊂KF.

例1在知识空间

K={∅,{a},{a,b},{b,c},{a,b,c}}

中，{a,b,c}={a}∪{a,b}∪{b,c}，则由推论3得{a,b,c}不是原子.而{a,b}不能由其非空真子集的并表示，由推论2得{a,b}是原子;同理,{a},{b,c}都是原子.因此，该知识空间的知识基B={{a},{a,b},{b,c}}.或者由Dowling[4]算法也可得出,问题a只有一个原子{a}，问题b有两个原子{a,b}和{b,c}，问题c的原子为{b,c}，该算法[4]的计算复杂度为O(|K|2|Q|).

2.2 在反知识背景中的原子特征和知识基

定义11设(P,Q,Ic)为反知识背景，p∈P，若满足

则称p为并可约元;否则,称p为并不可约元.

由知识空间(Q,K)满足并封闭，可得性质2.

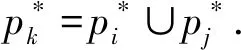
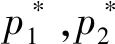
定理2设(Q,K)为知识空间，(P,Q,Ic)为其反知识背景，知识状态∅≠K∈K与p∈P对应.则

1) 知识状态K不是一个原子,当且仅当p是并可约元;

2) 知识状态K是一个原子，当且仅当p是并不可约元.

由推论2和推论3易证.

推论4设LJ(P,Q,Ic)={p*|p∈P}{∅}，OJ(P,Q,Ic)={p*|p是并可约元}，则LJ(P,Q,Ic)

表1 由K导出的反知识背景Tab.1 Anti-knowledge context derived by K

OJ(P,Q,Ic)是原子的全体，即为知识空间(Q,K)的知识基.

例2由知识空间

K={∅,{a},{a,b},{b,c},{a,b,c}}

性质4设(Q,K)为知识空间，(P,Q,Ic)为其反知识背景.对于∀αi,αj∈RIc，则∃αk∈RIc,得αk=αi+αj.

由定义2可知，知识空间(Q,K)满足K对有限并封闭，易得性质4，则RIc满足对加法封闭.找出集合RIc的一个基，就可得到知识空间的原子和知识基.

性质5设(Q,K)为知识空间，(P,Q,Ic)为其反知识背景.对于α∈RIc，假设α=∑αi∈RIcαi，则α≥αi.

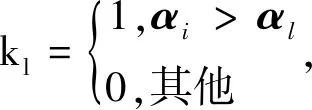
定理3设(Q,K)为知识空间，(P,Q,Ic)为其反知识背景，知识状态∅≠K∈K与α≠0∈RIc对应.则

1) 知识状态K不是一个原子，当且仅当α是并可约元；

2) 知识状态K是一个原子，当且仅当α是并不可约元.

推论5设RJ={α|α∈RIc是并可约元}，则由RIcRJ可找出所有原子，即知识空间(Q,K)的知识基.

定理4设(Q,K)为知识空间，(P,Q,Ic)为其反知识背景及其关系矩阵MIc，则知识基所含元素的个数(即原子的总个数)为矩阵MIc的行秩.

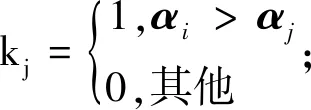
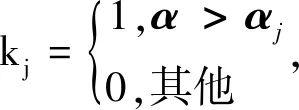
2.2.3 基于布尔矩阵的原子特征和知识基 由知识空间(Q,K)满足并封闭，则其对应的反知识背景(P,Q,Ic)中，{p*|p∈P}也满足并封闭.此时，反知识背景不是节1.2意义上的形式背景，但仍然沿用其中的一些名称和记号，例如，关系矩阵和对象关系矩阵等.从布尔矩阵的角度获取原子的特征，有两种方式.结合定义12和定理3，给出第一种矩阵运算方法，具体过程如下.

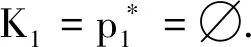
定理5设(Q,K)为知识空间，(P,Q,Ic)为其反知识背景，G为其对应的知识状态真包含关系矩阵，S为其对应的知识状态线性表示矩阵，Sd为其对应的原子的特征矩阵，则

2)S中的第i个行向量为α(pi)；

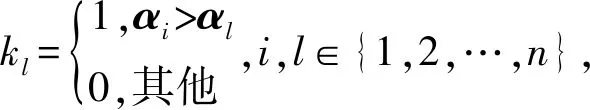
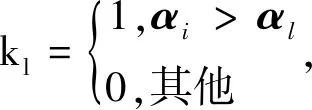
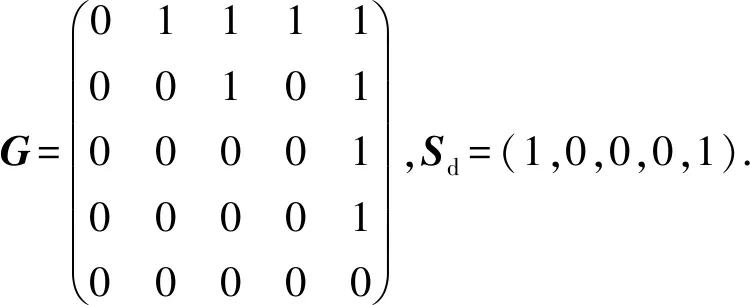
算法1在反知识背景(P,Q,Ic)中获取原子和知识基的矩阵算法1

输入：反知识背景(P,Q,Ic)，二元关系矩阵MIc，并且|P|=n，|Q|=m.

输出：原子和知识基.

步骤1： 计算对象关系矩阵Mn×n.

步骤2： 计算矩阵S和Sd.

因为问题q的原子是在包含关系下的状态集族的极小集，而这种关系也可用布尔矩阵运算实现，即第二种矩阵方法，具体过程如下.

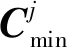
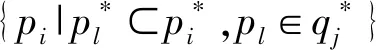
表2 由表1更新得到 的极小关系矩阵Tab.2 Minimal matrix obtained by updating Table 1

算法2在反知识背景(P,Q,Ic)中获取原子和知识基的矩阵算法2

输入：形式背景(P,Q,Ic)，二元关系矩阵MIc，并且|P|=n， |Q|=m.

输出：形式背景的所有原子和知识基.

步骤1： 计算对象关系矩阵Mn×n.

步骤2： 计算知识状态集族的极小集

forj= 1:|Q|

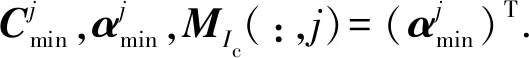
end for

Mmin=MIc.

2.3 在知识背景中的原子特征和知识基

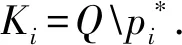
类似地，在知识背景中也可从算子和布尔矩阵的角度刻画原子特征，构建知识基.

2.3.1 基于算子的原子特征和知识基

定义15设(P,Q,I)为形式背景，p∈P，若满足

则称p为交可约元；否则，称p为交不可约元.

定理7设(Q,K)为知识空间，(P,Q,I)为其知识背景，知识状态∅≠K∈K与p∈P对应.则

1) 知识状态K不是一个原子，当且仅当p是交可约元；

2) 知识状态K是一个原子，当且仅当p是交不可约元.

推论6设LM(P,Q,I)={p*|p∈P}{Q}，OM(P,Q,I)={p*|p是交可约元}，则LM(P,Q,I)OM(P,Q,I)是原子的全体，即为知识空间(Q,K)的知识基.

2.3.2 基于布尔矩阵的原子特征和知识基 在知识背景(P,Q,I)中，可通过算子 “”,“”和“”获取原子[26].

定义16[26]在知识背景(P,Q,I)中，定义算子“”,“”和“”.其中，pq表示pIcq并且p*是不包含q的极大集;pq表示pIcq并且q*是不包含p的极大集;pq表示同时满足pq和pq.

定理8设(Q,K)为知识空间，(P,Q,I)为其知识背景.在(P,Q,I)中,每一个问题q∈Q对应的“”的知识状态就是它的原子.

证明：若pq，则pIcq，且p*是不包含q的极大集.因此，Qp*是包含q∈Q的知识状态中的极小集.故Qp*为q的一个原子.

定理9[26]设(Q,K)为知识空间，(P,Q,I)为其知识背景.在(P,Q,I)中,每一个问题q∈Q对应的“”的知识状态是一个原子.

例7由知识空间

K={∅,{a},{a,b},{b,c},{a,b,c}}

表3 由K导出的知识背景Tab.3 Knowledge context derived by K

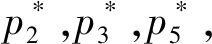
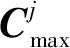
例8Korossy[26]选取了初等几何学中与毕达哥拉斯定理有关的5个问题，记为Q={1,2,3,4,5}，通过实验测试并分析得到知识空间(Q,K)，其中，

由该知识空间导出的知识背景,如表4所示.

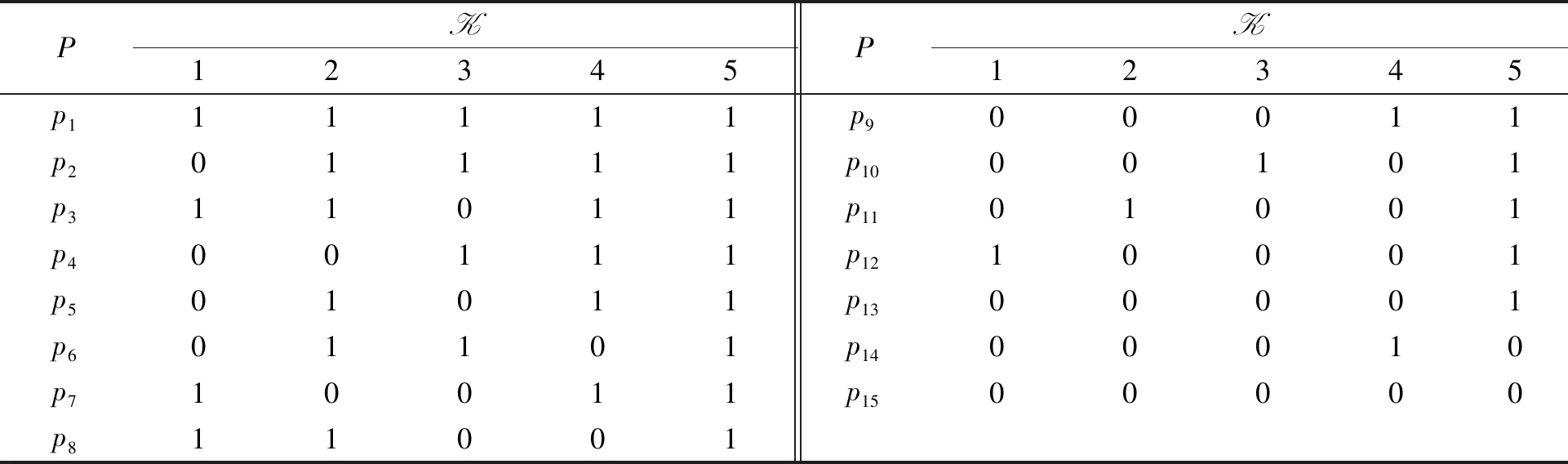
表4 由K导出的知识背景Tab.4 Knowledge context derived by K

利用定理10对知识背景的关系矩阵MI中的所有列进行对象内涵的极大运算，最后,可以得到的新的布尔矩阵，记为Mmax.Mmax中所有二元对(取值为零)对应着pq关系下的极大集，在二元对取值为零处的问题q对应的知识状态K=Qp*为问题q的原子，所有原子组成该知识背景所对应的知识空间的知识基.由Mmax可得出例7中知识空间的所有原子对应的二元对(取值为零)和原子，如表5所示.所以,该知识空间(Q,K)的知识基为

B={{1},{3},{1,2},{2,3},{1,4},{3,4},{1,2,3,5}}.

表5 问题q对应的二元对及其原子Tab.5 Pairs and atom of question q

算法3在知识背景(P,Q,I)中获取原子和知识基的矩阵算法

输入： 知识背景(P,Q,I)，二元关系矩阵MI，并 且|P|=n，|Q|=m.

输出： 知识背景的所有原子和知识基.

步骤1： 计算对象关系矩阵Mn×n.

步骤2： 计算对象内涵的极大集

forj=1:|Q|

end for

Mmax=MI.

文中提出的矩阵算法1、算法2和算法3都可以得到知识空间的原子和知识基，计算的时间复杂均为O(|Q||K|2).

3 结束语

先建立知识空间与反知识背景、知识背景之间的关系，再从并不可约元、交不可约元、集合的包含关系等方面判定原子特征，进而从知识状态、算子、布尔向量和布尔矩阵等不同角度，获取原子和知识基.在3种矩阵算法中，算法1通过矩阵方法计算并不可约元，获得原子和知识基，该算法还可以得到并可约元的并式表达式；算法2用矩阵方法计算出集合在包含关系下的极小集，从而得到各个问题的原子，构建知识基；算法3用矩阵方法计算出集合在包含关系下的极大集，从而获得pq，进而得到各个问题的原子和知识基.文中提出的矩阵方法为知识空间的研究拓展了计算方法，后续可进一步研究形式背景与知识空间的关系，并将它们相互结合应用到教育教学等领域.