火灾下两种不同边界钢筋混凝土双向板的振动性能分析

朱三凡， 董毓利， 段进涛， 叶森贵

(1. 华侨大学 土木工程学院， 福建 厦门 361021；2. 健研检测集团有限公司， 福建 厦门 361004)

在火灾作用下，钢筋混凝土板内的温度发生变化，从而在板内产生温度应变和温度应力.由于钢筋混凝土板内的温度场是与时间相关的非线性瞬态温度场，所以会导致结构的振动，即热致振动[1].现有研究发现在火灾作用下结构及构件的振动有很明显的自激励振动特性[2].

索亮[2]对足尺钢筋混凝土双向板进行恒载下受火试验，采用测振仪对火灾过程中双向板的振动特性进行测量，研究火灾下双向板振动特性的变化情况，分析振动信号的频率结构组成.朱崇绩[3]研究火灾下邻边简支邻边固支双向板、仅在柱上有梁的双向板楼盖和平板无梁楼盖的振动特性及频率变化，并通过回归分析给出火灾下3种板的频率与板中竖向位移的关系式.王为等[4]对足尺寸钢框架的二层楼面板进行火灾试验，研究表明加速度振动信号强度和板边约束有很大关系，可以通过振动信号监测混凝土板裂缝的开展情况.史春辉等[5]通过ABAQUS软件对高温下钢筋混凝土简支板进行动力特性分析，得出高温下钢筋混凝土简支板温度场的分布规律，并在此基础上分析配筋率对钢筋混凝土板固有频率的影响，以及温度场对简支板固有频率的影响，进一步建立温度场下钢筋混凝土简支板固有频率与混凝土损伤深度之间的对应关系.王剑[6]对钢筋混凝土简支单向板和四边简支双向板进行火灾下(后)的振动特性分析，并通过火灾后的承载力和共振考虑其安全性能.刘才玮等[7]对4根足尺混凝土简支梁进行火灾前及60，90，120，150 min的受火试验，研究火灾下结构振动发展规律，拟合火灾下基频衰减公式.以上研究表明，不同的边界条件会影响火灾下混凝土双向板的振动性能.

本文对以往研究未涉及的两种边界条件(三边简支一边固支、两短边固支两长边简支)足尺钢筋混凝土双向板进行火灾试验，分析火灾下双向板的振动性能.

1 试验概况

1.1 试件设计

共设计4块足尺钢筋混凝土双向板(双向板ES1(ES1-1，ES1-2)，双向板ES2(ES2-1，ES2-2))，火灾炉框架轴线尺寸为7 150 mm×5 650 mm(长×宽),燃烧空间尺寸为6 550 mm×5 050 mm(长×宽)，混凝土强度为C30.试验构件参数，如表1所示.表1中：η为含水率.按照GB/T 50152-2012 《混凝土结构试验方法标准》[8]进行支座设置及嵌固端装置设计，分级施加2.0 kPa的均布荷载.荷载施加完毕30 min后，开始进行火灾试验，升温曲线参照国际标准组织制定的ISO-834标准升温曲线.火灾试验炉照片，如图1所示.加载块布置图，如图2所示.

表1 试验构件参数Tab.1 Parameters of test component

1.2 加速度传感器的布置

在双向板板面布置振动测点，板面加速度传感器及其布置图,如图3，4所示.图4中：V1～V3为振动测点.

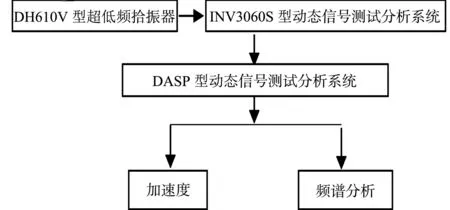
图5 动态信号测试分析系统Fig.5 Dynamic signal test and analysis system

在火灾作用下,混凝土板顶温度越来越高，为防止拾振器在高温下发生损坏，在加速度传感器与双向板之间设置耐火砖.先用水泥砂浆将耐火砖固定在板上，再将传感器粘结到耐火砖上.试验时,双向板振动的加速度信号通过DH610V型超低频拾振器、INV3060S型动态信号测试分析系统进行采集.采集的数据通过DASP型动态信号测试分析系统及试验模态分析软件进行分析.动态信号测试分析系统，如图5所示.

2 结果及分析

2.1 加速度时程分析

整个试验过程中，双向板板面加速度(a)的变化可以分为3个阶段，以双向板ES1-1为例进行说明.双向板ES1-1的加速度时程曲线(V2测点)，如图6所示.结合图6及试验过程可得以下3个结论.1) 第1阶段为平稳期，从试验开始到第10 min.这个阶段双向板受火灾激励影响不大，加速度平稳.2)第2阶段为激烈期，从第10 min到第50 min.这个阶段双向板底面受火膨胀，截面存在较大的升温梯度，受固支端约束，板面产生大量裂缝且发展很快，板中竖向位移增速很快，双向板的损伤导致刚度迅速降低，竖向一阶自激励频率出现明显变化.3) 第3阶段为稳定期，从第50 min到试验结束.这个阶段板面基本不出现新的裂缝和板底爆裂，已有裂缝仍继续扩展，双向板的加速度相对平稳.

图6 双向板ES1-1的加速度时程曲线(V2测点)Fig.6 Acceleration time history curves of two-way slab ES1-1 (V2 measuring point)

2.2 频谱分析、频率变化与位移关系曲线

采用全程分析(平均计算)，傅里叶变换(FFT)分析点数为2 048，加窗形式为汉宁窗，平均方式为线性平均.经过傅里叶变换后，双向板ES1-1的实测频谱图，如图7所示.图7中：f为频率；fv为竖向一阶自激励频率.双向板竖向一阶自激励频率、板中竖向位移(sv)与时间的变化关系，如图8所示.整个试验过程中，双向板竖向一阶自激励频率的变化可以分为3个阶段.

(a) 试验前(未施加均布荷载) (b) 试验前(施加均布荷载)

(c) 受火后第10 min (d) 受火后第60 min

(e) 受火后第90 min (f) 受火后第120 min

(g) 受火后第150 min (h) 停火时 图7 双向板ES1-1的实测频谱图Fig.7 Measured spectrogram of two-way slab ES1-1

1) 第1阶段，从试验开始到第60 min.这个阶段双向板底面受火膨胀、截面存在较大的升温梯度，受固支端约束，板面产生大量裂缝且发展很快，板中竖向位移增速很快，双向板的损伤导致刚度迅速降低，竖向一阶自激励频率出现明显变化.

2) 第2阶段，从第60 min到第150 min.这个阶段板中竖向位移增速趋缓，竖向一阶自激励频率的降速相应地发生变化，板面基本不产生新的裂缝，已有裂缝仍不断扩展；随着双向板中心区域面内薄膜效应逐渐由压变为拉，受拉薄膜效应逐渐发展，板中竖向位移增速变慢，刚度衰减速度较第1阶段大幅降低.

3) 第3阶段，从第150 min到试验结束.这个阶段竖向位移缓慢地线性增加，竖向一阶自激励频率降幅很小，反映刚度衰减缓慢.在整个试验过程中，双向板的竖向一阶自激励频率衰减幅度较大，说明在火灾作用下双向板的刚度有较大损失.

(a) 双向板ES1-1 (b) 双向板ES1-2

(c) 双向板ES2-1 (d) 双向板ES2-2 图8 竖向一阶自激励频率、板中竖向位移与时间的变化关系Fig.8 Variations of vertical first-order self-exciting frequency， vertical displacement in slab and time

2.3 竖向一阶自激励频率与板中竖向位移的关系

双向板竖向一阶自激励频率与板中竖向位移的变化规律具有一致性(图8).火灾下，双向板ES1,ES2的竖向一阶自激励频率-板中竖向位移曲线，如图9，10所示.图9，10中：R2为线性相关率.

(a) 双向板ES1-1 (b) 双向板ES1-2图9 竖向一阶自激励频率-板中竖向位移曲线(双向板ES1)Fig.9 Curves of vertical first-order self-exciting frequency and vertical displacement in slab (two-way slab ES1)

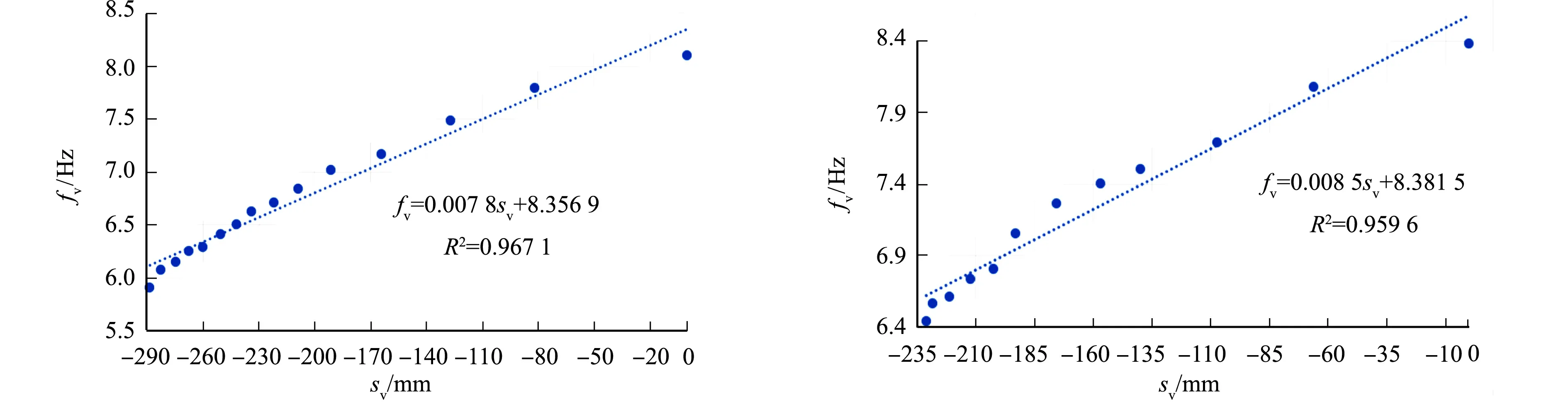
(a) 双向板ES2-1 (b) 双向板ES2-2图10 竖向一阶自激励频率-板中竖向位移曲线(双向板ES2)Fig10 Curves of vertical first-order self-exciting frequency and vertical displacement in slab (two-way slab ES2)

经拟合分析可得双向板ES1-1竖向一阶自激励频率与板中竖向位移的关系式为fv=0.005 3sv+8.422 8，双向板ES1-2竖向一阶自激励频率与板中竖向位移的关系式为fv=0.005 1sv+8.262 8，双向板ES2-1竖向一阶自激励频率与板中竖向位移的关系式为fv=0.007 8sv+8.356 9，双向板ES2-2竖向一阶自激励频率与板中竖向位移的关系式为fv=0.008 5sv+8.581 5.

将两块双向板的竖向一阶自激励频率与板中竖向位移拟合公式的平均值作为关系式[3]，将同一边界条件双向板竖向一阶自激励频率与板中竖向位移进行拟合，结果如图11所示.图11中：fv，ES1，fv，ES2分别为双向板ES1，ES2的竖向一阶自激励频率；sv，ES1，sv，ES2分别为双向板ES1，ES2的板中竖向位移.

(a) 双向板ES1 (b) 双向板ES2图11 同一边界条件双向板的竖向一阶自激励频率-板中竖向位移曲线Fig.11 Curves of vertical first-order self-exciting frequency and vertical displacement in slab with same boundary conditions of two-way slab

双向板ES1，ES2的竖向一阶自激励频率-板中竖向位移的关系式，即

fv，ES1=0.005 2sv，ES1+8.350 1

，

(1)

fv，ES2=0.008 2sv，ES2+8.487 5

.

(2)

此外，考虑到实际工程中双向板的尺寸、配筋情况及受火前竖向基频的不同，将受火时间点与受火前的竖向一阶自激励频率的差值Δf(简称频率差值)替代受火时间点的竖向一阶自激励频率，拟合的频率差值与板中竖向位移曲线，如图12所示.图12中：ΔfES1，ΔfES2分别为双向板ES1，ES2的频率差值.

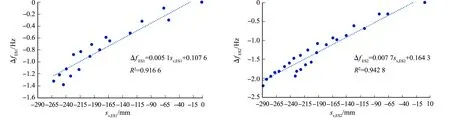
(a) 双向板ES1 (b) 双向板ES2图12 频率差值与板中竖向位移曲线Fig.12 Curves of frequency difference and vertical displacement in slab

双向板ES1，ES2的频率差值与板中竖向位移的关系式分别为

ΔfES1=0.005 1sv，ES1+0.107 6

，

(3)

ΔfES2=0.007 7sv，ES2+0.164 3

.

(4)

3 火灾下楼板耐火极限预警方法

当火灾发生时，在建筑物坍塌前提前做好预警工作是消防救援的重要课题.通常采用建立观察哨依靠肉眼进行观察、控制受火极限时间两种方法.文中基于楼板竖向一阶自激励频率差值Δf进行楼板耐火极限预警.

在火场中，可以通过非接触式监测仪器快速采集楼板结构的竖向自激励频率，通过频率差值进行火场安全预警.非接触式结构振动频率测试方法已有较深入的研究及工程应用，地基干涉雷达已被广泛地应用于建筑物、桥梁动力特性监测中[10-11]，文献[12-13]也提出基于机器视觉技术的非接触式结构动力特性识别方法.

将受火板板中竖向位移限值代入频率差值与板中竖向位移关系式，可以计算出楼板相应结构的频率差值限值，并以此作为火场安全预警指标.学者已对板中竖向位移限值进行了许多研究，Huang等[14]建议采用sv=l/20作为受火板的耐火极限准则，l为短跨跨径；Bailey等[15]发现配筋率低于8%的双向板发生破坏时，钢筋应力较高且裂缝较宽，进而导致较大的变形，当受拉钢筋达到极限应变0.01时[16]，双向板达到极限承载力；王勇等[17-18]提出低配筋率双向板跨中挠度达到l/20时，双向板即被破坏.

在实际工程中，双向板的配筋率一般不低于8%，因此，最终以sv=l/20作为两种边界条件下双向板的破坏准则.

1) 三边简支一边固支双向板.将式(3)进行转换后,可得

(5)

将sv，ES1=l/20代入式(5)，可得三边简支一边固支双向板火灾下的频率差值限值ΔfES1，lim为

ΔfES1，lim=2.55×10-4l+0.107 6

.

(6)

2) 两短边固支两长边简支双向板.将式(4)进行转换后，可得

(7)

将sv，ES2=l/20代入式(7)，可得两短边固支两长边简支双向板火灾下的频率差值限值ΔfES2，lim为

ΔfES2，lim=3.85×10-4l+0.164 3

.

(8)

4 双向板竖向一阶自激励频率的数值计算

4.1 受火前双向板竖向一阶自激励频率的数值计算

以双向板ES1-1为例，通过有限元软件ABAQUS对其受火前竖向一阶自激励频率进行计算.按照试验的实际情况建模[19]，混凝土板选用8节点实体单元C3D8，钢筋选用单元DC1D2，钢筋与混凝土之间的粘结通过将钢筋嵌入混凝土板内(embedded region)实现.双向板的边界条件为固支边约束板的竖向位移和水平位移，并施加支座负弯矩，简支边约束双向板的竖向位移.在自振频率分析步(step)中定义频率的提取分析步，特征值求解器选用Lanczos方法，使用基于SIM的线性动力学步骤.双向板ES1-1的数值计算模型，如图13所示.双向板ES1-1受火前的竖向一阶模态，如图14所示.

4.2 试验炉温

双向板ES1-1的温度曲线，如图15所示.图15中：θ为温度；tf为受火时间.由图15可知：双向板ES1-1的温度曲线与ISO-834标准升温曲线符合度较好.

双向板ES1-1板中沿厚度方向温度-时间曲线，如图16所示.图16中：θs为双向板温度;FS5-1～FS5-7为温度测点.

4.3 有限元模型的数值计算

双向板ES1-1的频率差值-时间曲线，如图17所示.双向板ES1-1的频率差值-板中竖向位移曲线，如图18所示.图18中：Δfs为频率差值的计算值；Δft为频率差值的实测值.由图18可知：火灾下双向板ES1-1的频率差值-板中竖向位移的实测值曲线与计算值曲线基本一致，这种有限元软件数值分析的方法可应用于其他不同规格尺寸的双向板.

频率差值的计算值与板中心竖向位移的关系式为

Δfs=0.005 3sv+0.072 8

.

(9)

频率差值的实测值与板中心竖向位移的关系式为

Δft=0.006sv+0.155 5

.

(10)

5 结论

1) 火灾下双向板板面加速度变化可分为平稳期、激烈期和稳定期3个阶段.

2) 火灾下双向板竖向一阶自激励频率的变化可以分为3个阶段，第1阶段频率降幅及降速均最大，第3阶段频率降幅及降速均最小.

3) 火灾下双向板竖向一阶自激励频率与板中心竖向位移的变化规律具有一致性，通过拟合分析可以建立板竖向一阶频率与板中竖向位移的关系式.

4) 提出火灾下两种边界双向板的频率变化预警限值的计算公式.

5) 通过有限元软件ABAQUS进行数值分析，火灾下双向板ES1-1的频率差值-板中竖向位移的计算值与实测值曲线基本一致.有限元软件数值分析的方法可应用于其他不同规格尺寸的双向板.