地面交通荷载对浅埋隧道的动力响应分析

杨宗桦， 孙杰， 陈士海

(1. 华侨大学 土木工程学院， 福建 厦门 361021；2. 济南城建集团有限公司， 山东 济南 250031)

为了预防地面交通荷载对隧道产生的振动损害，研究地面交通荷载对浅埋隧道的动力响应具有重要意义.众多学者对振动波在地层中的传播展开研究.Eason[1]通过对运动荷载作用下土体动应力分布的研究，得到地层中的一维解；De Barros等[2]利用波数积分法对运动荷载作用下的地层动荷载响应进行研究；Sneddon[3]利用位移积分法对运动荷载作用下的弹性模型进行求解,并给出积分形式的位移解;Pao等[4]针对波入射单层支护隧洞的问题，利用波数展开法讨论隧道结构的动力响应分布；Davis等[5]引入大圆弧假定，给出入射波在无支护洞室时的衍射解;Forrest[6]提出由土壤包围的无限长壳模型，用来计算地下列车引起的地基振动问题.而对于地面移动荷载振动作用下引起的隧道结构动力响应问题，文献[7-8]采用格林函数法解决粘弹性体各种动荷载作用下的响应问题，取得了突破性进展；戚桂峰等[9]采用格林函数法得到铁轨交通荷载作用下土层的振动解析解；曾晨等[10]采用空间饱和土三维隧道衬砌振动模型，对地面交通载荷作用下地层土的动力反应特点进行研究；罗红星等[11]建立有限元数值模型，分析地面交通荷载下浅埋隧道围岩变形的影响；郑余朝等[12]建立三维数值模型，得出列车荷载下穿隧道的拱顶压力随埋深变化的规律；蒋博林等[13]结合数值模拟分析和正交试验,分析各计算参数对悬浮隧道跨中竖向振动位移的影响；文献[14-15]研究地面交通荷载引起浅埋隧洞的振动问题，首次给出半空间隧洞的动力响应解析解；青松勇等[16]采用有限元分析的方法，分析飞机滑动荷载作用下对既有地铁的动荷载分布规律；范昌杰[17]选用有限元分析的方法给出地面交通荷载影响下的隧洞变形规律；赵俊澄等[18]采用数值模拟的方法，研究是否考虑交通荷载时隧道上方的路基沉降差值.

目前，分析车辆荷载对地下隧道的动应力问题通常采用数值模拟的方式.为了对数值模拟的结果进行验证，本文进行理论推导，建立三维弹性半空间浅埋圆形隧道数学模型，研究移动荷载作用下圆形隧道在弹性半空间的动力响应问题，并分析不同车速和埋深对响应的影响.

1 工程概况

济南市顺河快速路南延(英雄山立交至南绕城高速)建设工程,是构建济南市快速路路网骨架的重要组成部分,承担着主城区对外进出交通的快速集散任务，同时承担着重要的公共交通走廊功能.项目北起英雄山立交, 南至南绕城高速，全长约5.1 km.主线采用浅埋隧道形式,全长2.2 km，双向6车道，分左右线布设.地下道路工程暗挖段采用小净距隧道的结构形式，左、右线间最大净距25 m,最小净距为北端洞口7 m，南端洞口5 m，全线最小圆曲线半径1 350 m，最大圆曲线半径13 000 m.隧道纵断线形为W形，符合现状地面道路走势，以暗挖段最大埋深13 m为控制原则，两端明暗挖分界线位置埋深3～4 m.隧道拱顶位置处围岩属于第四系黏性土、碎石土，洞身地层岩性以第四系碎石、黏性土为主，根据《公路工程地质勘察规范》规定，隧道围岩分级为Ⅴ级.初期支护由工字钢拱架、径向锚杆、钢筋网及喷射混凝土组成.围岩和初期支护的参数，如表1所示.表1中：E为弹性模量;ρ为密度;ν为泊松比;d为支护结构厚度.

表1 介质参数Tab.1 Medium parameters

图1 移动荷载作用下的隧道模型Fig.1 Tunnel model under moving load

移动荷载作用下的隧道模型，如图1所示.图1中：P(t)为移动集中简谐荷载;v为移动速度；h为隧道结构中心与地面的距离；X为隧道埋深；点O，O1分别为荷载地面作用点、隧道圆心；θ，r分别为坐标系(r，θ)的极角值和极轴；φr,ψr,φ11,ψ11,φ12,ψ12表示围岩处产生的势函数；φ21,ψ21,φ22,ψ22表示支护内产生的势函数；r1,θ1分别为隧道内圆心坐标系的极径和极轴；隧洞内半径取6.9 m，初支厚度取0.35 m.在z=0平面上,沿x轴正方向以速度v匀速运动的列车的移动集中荷载可表示为

P(t)=P0eiω0tδ(x-vt)δ(y).

(1)

式(1)中：t为车辆经过点O的时间;ω0为荷载变化的圆频率；P0为车子总荷载；δ(y)为单位脉冲函数.

2 基本方程

在弹性介质里，机械扰动的传播形成弹性波动，简称弹性波.弹性波理论主要研究波的产生与传播的规律，进而弄清弹性介质的位移矢量场、应力及应力张量场随时间变化的情况.已知各向同性的弹性半空间体用位移表示的运动方程[9]为

(λ+μ)∇θ+μ∇2u+ρL=ρ∂2u/∂t2

.

(2)

式(2)中：L为土体体力,令L=0；u为土体位移；λ，μ为拉梅常数；∇为哈密顿算子；∇2为拉普拉斯算子.

根据斯托克斯-亥姆霍兹定理进行分解，式(2)的解可以表示为

u=up+us=∇φ+∇×ψ.

(3)

式(3)中：φ为位移的标量势；ψ为位移的矢量势，ψ=(ψ1,ψ2,ψ3)，且ψ3=0.

矢量势函数满足广义规范条件∇·ψ1=0,代入式(2)可得

(4)

若荷载关于θ=0对称，利用分离变量法对方程(4)进行求解,可以得到围岩中的势函数表达.

3 弹性半空间内隧道的动力响应分析

3.1 围岩中极坐标系下的波函数展开

振动位移在围岩中产生的波势函数，基于入射波动方程(∇2+k2)φ=0，引入极坐标系，并利用分离变量法得到围岩中的势函数为

(5)

图2 分层界面上入射波反射和折射Fig.2 Reflection and refraction of incident waves at layered interface

由于围岩、支护、隧道内部间存在分界面，入射波在分界面上一般各形成2个反射波P波、SV波和2个折射波P波、SV波,如图2所示.若不考虑波在弹性空间中的耗散，频率为ω的入射弹性波位移势函数可表示为

φj(x,z)=A0exp[k0,α(xsinθα-zcosθα)-iωt].

(6)

式(6)中：k0,α为入射波波数，k0,α=ω/c0,α，c0,α为入射波波速,ω=2πf，f为入射波频率；θα为P波入射角度；t为时间变量；j为自然数.

利用直角坐标系(x,z)与(x1,z1),极坐标系(r,θ)之间关系为

(7)

(8)

弹性波入射势函数在极坐标系下表达式级数展开为

(9)

式(9)中：系数A0,n,B0,n,C0,n,D0,n可以表示为

反射P波和SV波的反射系数由边界条件确定，k0,α=ω/c0,α，k0,β=ω/c0,β，sinθα/c0,α=sinθβ/c0,β.θβ代表反射SV波的反射角，满足Snell反射定律[19].n=0，ε=1；n>1，ε=2.反射系数k1和k2分别为

3.2 围岩与支护中的势函数表达

在文中模型中，除了反射的P波和SV波外,入射波在围岩与衬砌交界处还存在散射波，利用波函数展开法,可将位移势函数转换为级数形式.入射波通过围岩和支护分界时，将在界面上产生反射P波和反射SV波.

1) 围岩中的势函数可表示为

(10)

为简化散射波的研究，采用大圆弧假定，其产生的散射势函数为

(11)

2) 在初期支护中产生的散射波对应的势函数表示为

(12)

在隧道内产生的散射势函数为

(13)

式(10)～(13)中：kj,α,kj,β(j=1,2)分别为对应介质中P波和SV波的波数，kj,α=ω/cj,α，kj,β=ω/cj,β,cj,a,cj,β(j=1,2)分别为对应介质中P波和SV波的波速；Hn为Hankel函数;Jn为第一类Bessel函数.

因此，围岩、支护的总势函数可分别表示为

(14)

(15)

上述波函数表达式均为无穷级数形式，因此,在具体计算中必须考虑求解的精度问题，对无穷级数进行截断，尽可能地减少截断误差.当计算项数取n=7时，可满足计算精度的要求.

3.3 位移及应力响应的表达式

围岩内位移和应力表达为

(16)

(17)

3.4 边界条件

1) 边界条件1.根据界面应力和位移连续条件，在隧道围岩与支护界面r1=7.25 m处存在

(18)

2) 边界条件2.在隧道初支内表面r1=6.9 m处存在

(19)

利用边界条件求解上述方程组,即可确定待定系数的值，将待定系数代入式(14),(15)，可确定隧道围岩、支护内的势函数，将其代入式(16),(17)，可得到隧道围岩、支护的位移及应力响应分布.

4 结果分析

4.1 隧道围岩和支护的动力响应

在建立的数学模型中，地面移动荷载P(t)作用下会使土体内任意点产生振动位移.采用圆形隧道模型，关于振动波在圆形隧道结构的传播问题，可采用贝塞尔函数方程解决圆形或环形结构中的波动问题.考虑到振动波在隧道分界面传播时发生的反射和折射现象，将振动产生的位移势函数φ以贝塞尔函数的级数形式展开，结合边界条件求出待定系数后，可以得到总势函数表达，代入式(17)分别求出隧道围岩和支护的径向应力和切向应力，最后给出隧道的动力响应空间分布曲线图.

取P0=100 kN，v=100 km·h-1，E=1.3 GPa，ν=0.31作为模型计算参数，计算地面移动荷载作用下隧道围岩r1=7.25 m处的动力响应.围岩径向应力响应空间分布,如图3所示.由图3可知：隧道围岩0°拱顶处径向应力达2 705 Pa，围岩90°拱侧处径向应力达145 Pa，围岩底部可达470 Pa，表明隧道在拱顶和拱底处均会受到较大的径向应力；径向应力随着角度先急速减小再逐渐增大，并在隧道两侧处达到径向应力最小值.

围岩切向应力响应空间分布,如图4所示.由图4可知：隧道拱顶0°～90°位置处受到较大的切向应力；在θ=15°位置处受到的切向应力最小，且θ=60°拱侧处引起的最大动力响应达到576 Pa，表明隧道拱顶和两侧位置均会受到较大的切向应力.

图3 围岩径向应力响应空间分布 图4 围岩切向应力响应空间分布 Fig.3 Spatial distribution of radial stress response of surrounding rock Fig.4 Spatial distribution of circumferential stress response of surrounding rock

地面移动荷载作用下，隧道支护的动力响应分布曲线,如图5所示.由图5可知：地面移动荷载作用下隧道支护的拱顶处会引起较大的动力响应.除了拱顶外，隧道底部也会引起一定的动力响应.而支护受到的切向应力值远小于径向应力值，应对后者进行重点分析.对分析的结果进行假设，隧道支护结构在受到地面移动荷载的作用下，支护的顶部和底部位置处容易引起振动效应，从而导致结构的变形.

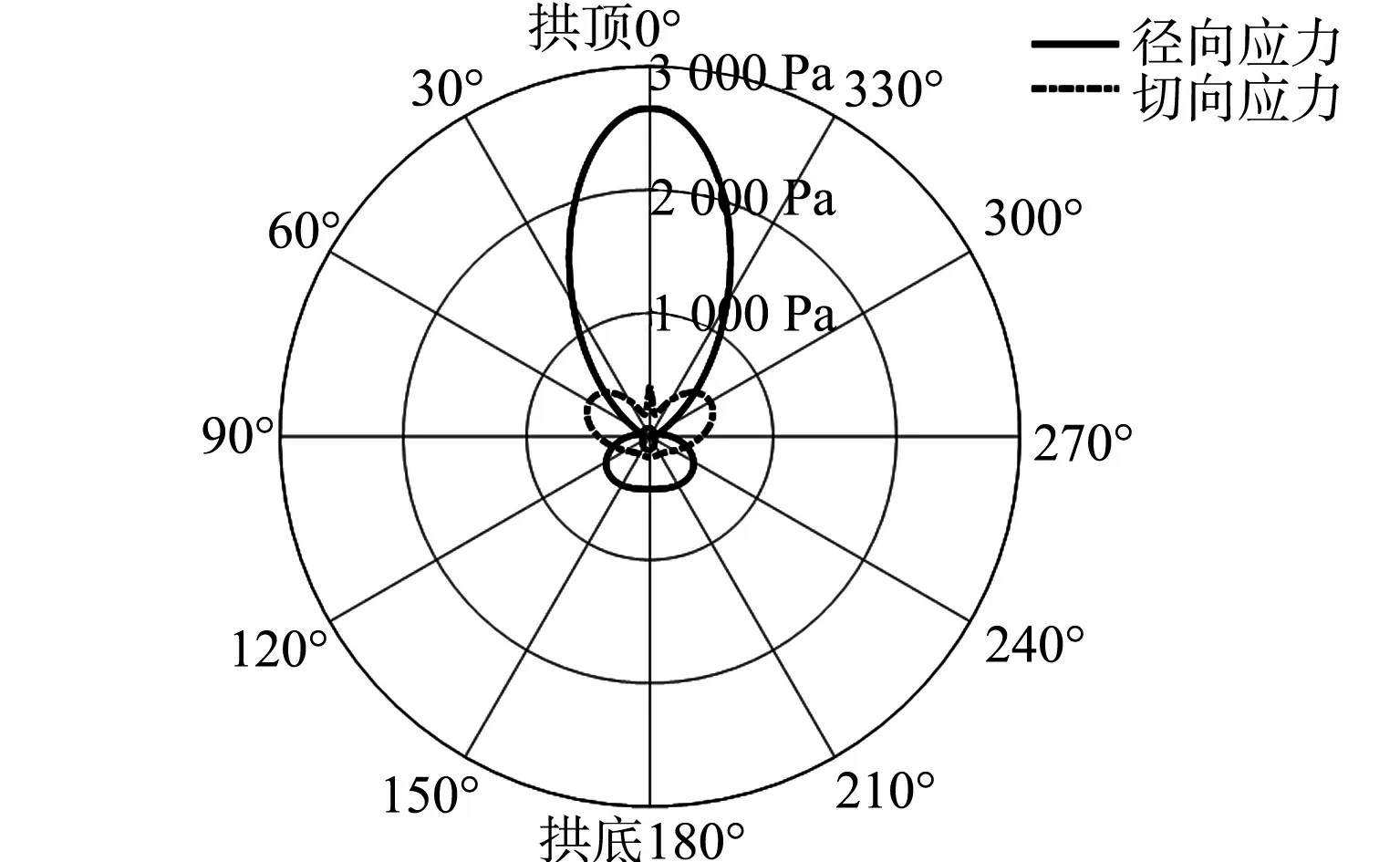
图5 支护的动力响应空间分布Fig.5 Spatial distribution of dynamic response of support

4.2 动力响应影响因素分析

为分析不同速度的荷载作用下隧道结构动力响应变化规律，选取隧道埋深X=10 m，移动荷载速度v分别为60,100,150 km·h-1，车辆荷载P0=100 kN，t=0.3 s作为模型计算参数.不同移动荷载速度时，隧道支护结构动力响应空间分布，如图6(a)所示.由图6(a)可知：随着荷载速度的增大；其径向应力值明显增大.从隧道顶部到底部，径向应力值先迅速降低再逐渐增长，并在拱腰处达到最小响应.可见当隧道埋深较浅时，地面荷载速度对下穿隧道的动力响应有显著影响，当荷载速度不断增大，隧道结构的动力响应会呈倍数增长.

分析不同埋深下隧道结构的动力响应变化，选取隧道埋深分别为10,15,20 m，P0=100 kN，v=100 km·h-1，t=0.3 s.不同隧道埋深时，隧道支护结构动力响应空间分布，如图6(b)所示.由图6(b)可知：随着隧道埋深的增大，其径向应力值随之减小，说明隧道埋深越深，受到地面移动荷载的影响就越小.

(a) 不同移动荷载速度 (b) 不同隧道埋深 图6 不同移动荷载速度和不同隧道埋深下的隧道支护结构动力响应空间分布Fig.6 Spatial distribution of dynamic response of tunnel support structure under different moving load velocities and different buried depths

基于结果的分析，提出以下假设：浅埋隧道在受到地面交通荷载作用时，隧道结构的拱顶处会引起较大的响应.在受到长期地面交通荷载的作用下，隧道拱顶位置处的支护结构要比其余位置更容易受到振动影响，从而导致支护结构的使用寿命减少，甚至产生破坏.由于隧道结构引起的径向应力值远大于切向应力值，故径向应力值可以作为分析浅埋隧道受到地面交通荷载作用下支护结构损坏的一个重要参考值.对地面荷载速度和隧道埋深等因素的分析中，浅埋隧道结构的动力响应对地面荷载速度的变化比较敏感.地面车辆速度过快会使地下浅埋隧道结构的动力响应快速增长，对隧道结构产生不良影响.

图7 有限元模型图Fig.7 Finite element model diagram

5 数值模型的验证

利用MIDAS软件建立的有限元网格尺寸如下：模型宽度为100 m，深度为100 m，厚度为4 m，地层和隧道结构各项参数均严格按照文中数学模型建立，并采用简化的单一岩层计算和摩尔-库伦本构模型.有限元模型，如图7所示.模型宽度方向的网格尺寸设置为1 m；模型深度方向网格划分采用线性梯度法，网格起始长度为1 m，结束长度6 m；模型100 m深度处，网格尺寸设置为6 m；初期支护外侧(靠近围岩侧)网格划分尺寸为0.76 m，共划分60段，初期支护内侧网格划分尺寸为0.72 m，共划分60段.建立模型的弹性边界，并进行特征值分析.汽车移动速度为100 km·h-1，轴距为6 m，从模型一端运动到另一端，将根据理论计算出的轴荷载输入模型.

求解类型设置为线性时程(直接积分)；时间步骤定义为总持续时间为3.6 s，时间步骤为100步；将上述计算得到的两个特征值0.491 437 2，0.164 859 4 s分别填入“分析控制”中“动力分析”所对应的“模态1”与“模态2”对话框中；最后，进行求解计算.

图8 围岩的径向应力云图Fig.8 Radial stress nephogram of surrounding rock

图9 围岩的切向应力云图Fig.9 Circumferential stress nephogram of surrounding rock

图10 围岩的切向应力对比图Fig.10 Contrast diagram of circumferential stress of surrounding rock

围岩的径向和切向应力云图，如图8，9所示.由图8,9可知：拱顶和拱底位置处产生的振动变形和动力响应较为明显，拱侧位置的动力响应较小，得到与理论结果相似的动力响应规律；计算得到拱顶最大径向应力为2 897 Pa，最大切向应力为637 Pa，与理论计算值进行对比，两者的误差范围均控制在15%以内，验证了理论模型的合理性和准确性.

将数值模拟得到的切向应力数据与理论计算的结果进行对比，结果如图10所示.由图10可知：数值模拟得到的应力值总体上比理论值大，误差在允许范围内；而数值曲线的动应力分布规律基本与理论曲线一致.

6 结论

建立弹性半空间浅埋隧道模型，将地面车载模拟为移动集中简谐荷载，通过理论方法，研究移动集中简谐荷载作用下圆形隧道在弹性半空间的动力响应问题，得到以下4点主要结论.

1) 地面移动集中荷载作用下，从隧道顶部到底部，径向应力响应先迅速降低再缓慢增长，浅埋隧道拱顶和拱底位置处有较大响应，拱腰处达到最小值.隧道拱顶处最容易发生结构损坏.

2) 地面移动集中荷载作用下，浅埋隧道拱顶和拱腰位置处有较大切向应力响应，拱底处达最小值.

3) 在不同荷载速度下，随着荷载速度的增大，其结构受到的径向应力和切向应力响应明显增大.

4) 在不同隧道埋深下，随着隧道埋深的增大，其径向应力响应明显减小.