基于离散余弦变换的积分因子方法求解非线性Allen-Cahn方程

张荣培, 霍俊蓉, 杨程程

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

0 引 言

为描述晶体中的反相位边界运动, Allen和Cahn于1979年提出Allen-Cahn方程[1],可以用于描述铁合金溶液冷却过程中结晶固体相分离运动。它是一个二阶非线性抛物方程,对于不同的物理体系具有不同的自由能形式。Allen-Cahn方程及其各种变形在图像分析[2]、晶体的生长[3]、平均曲率运动[4]和随机扰动[5]等实际问题中都发挥着极为重要的作用。由于此类相场模型没有真解,所以采用有效的数值方法来进行模拟就显得尤为重要。

近年来,有很多专家和学者对Allen-Cahn 方程的数值逼近方法进行了研究,包括有限元方法[6],有限差分法[7]、谱方法[8-9]、间断有限元方法[10]和无网格方法[11]等。另外,在处理高维问题时,算子分裂方法[12]也是一种求解复杂问题的有效策略。

本文应用二阶中心差分方法离散Allen-Cahn方程,利用Kronecker积写出二维拉普拉斯算子的微分矩阵,得到一组非线性常微分方程组。接下来发展积分因子方法进行时间离散。在时间离散过程中,应用Kronecker积的性质将微分矩阵进行谱分解,结合快速余弦变换,可以快速地进行时间离散。

1 数值方法

本文考虑以下形式的非线性Allen-Cahn方程的数值解:

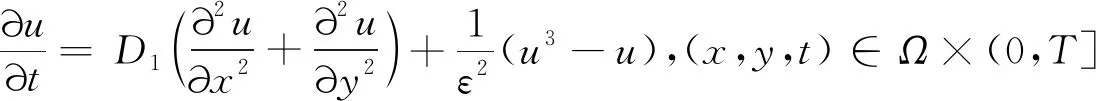
(1)

边界和初始条件如下:

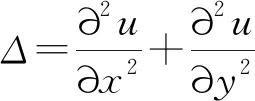
1.1 空间离散

设u在网格节点(xi,yj)的数值解为ui,j,由齐次Neumann边界条件,在网格内部点(xi,yj)和边界处的二阶导数差分格式分别为

定义离散解ui,j,1≤i≤Nx,1≤j≤Ny为Nx×Ny阶的矩阵U。由差分格(4)式和(5)式,得到该方程在x,y方向的微分矩阵分别为Bx和By,其中矩阵Bx为Nx×Nx阶的矩阵,(Bx)i,i=2,i=2,…,Nx-1,(Bx)i,i-1=-1,i=2,…,Nx,(Bx)i,i+1=-1,i=1,…,Nx-1,(Bx)1,1=(Bx)Nx,Nx=1,矩阵Bx中其他位置的元素均为0。同理有By为Ny×Ny阶的矩阵。

设Ix,Iy分别为Nx,Ny阶单位矩阵,将解矩阵向量化后得

U=vec(U)=(u1,1…uNx,1,u1,2…uNx,2,…,u1,Ny…uNx,Ny)T

(6)

利用(4)式～(5)式以及Kronecker积的定义,可以将(1)式的二阶中心差分格式写成如下形式:

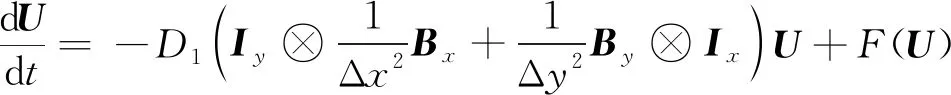
(7)

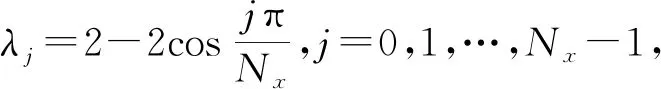
证明 首先考虑另外一个特征值问题:

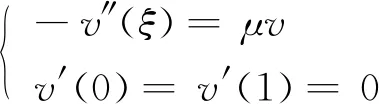
(8)

μ是特征方程的特征值,v为相应的特征函数。将求解区域离散成Nx个网格,

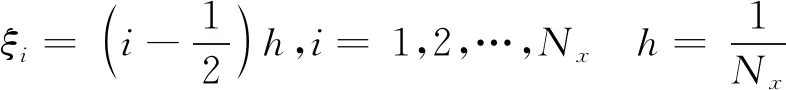
(9)

(8)式的特征方程为

λ2+μ=0

(10)

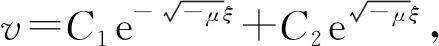
2) 当μ=0时,特征方程通解为v=C1+C2ξ,由条件(8),可得v=C1,求得特征值μ=0。

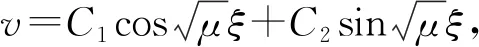
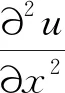
yj=(cosjπξ1,…,cosjπξNx)T,j=0,1,…,Nx-1

(11)

利用三角函数的和差化积公式可以验证Bxyj=λjyj,j=0,1,…,Nx-1,见附录。定理1证毕。

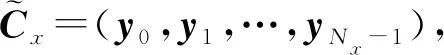
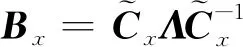
(12)

同理,对By也可得类似的结果。

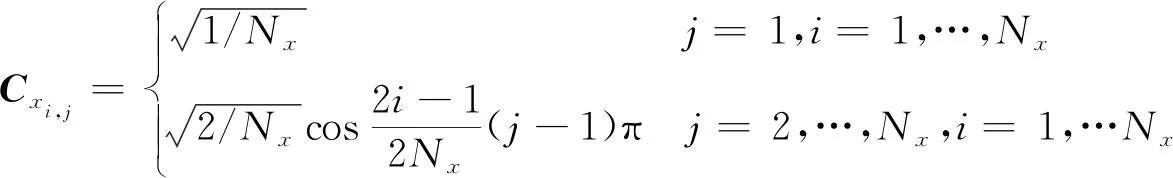
(13)

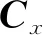
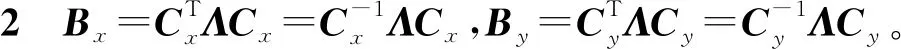
(14)

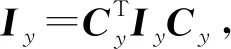
同理有

By⊗Ix=(Cy⊗Cx)-1(Λy⊗Ix)(Cy⊗Cx)

(16)

结合(15)式和(16)式可以得到

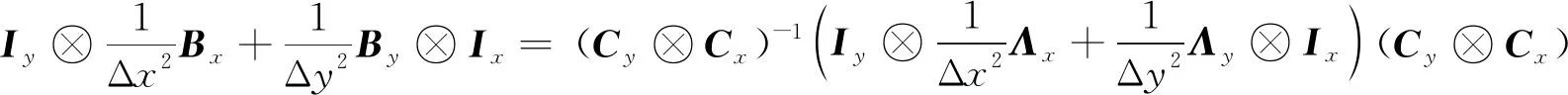
(17)

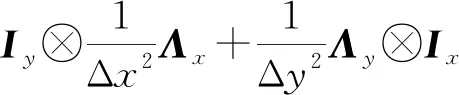
(18)

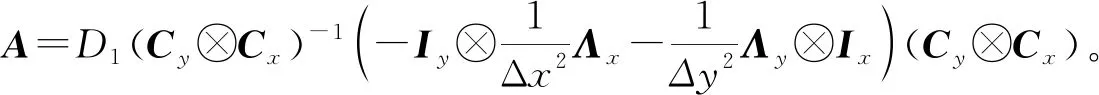
1.2 时间离散

下面应用积分因子法对(18)式进行求解,将(18)式两端同时左乘e-At,并从tn到tn+1=tn+Δt进行积分得到

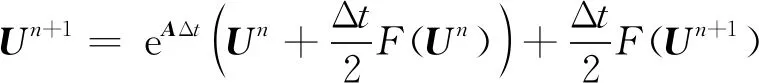
(19)

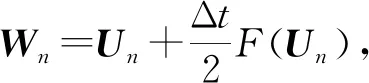
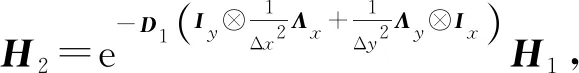
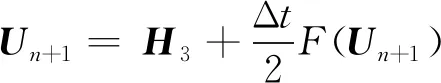
(20)

2 数值实验

应用本文提出的有限差分法和积分因子法求解下面的数值算例。考虑二维计算区域Ω=[-1,1]2,针对具有齐次Neumann边界条件的方程(1)进行求解。初值选取形状像哑铃的函数,见图1(a)所示。

选取参数ε=0.05,并在每个空间方向上取512个等分点,时间步长Δt=5×10-5。选取t1=3.53×10-2,t2=7.98×10-2,t3=1.18×10-1这3个时间点,数值结果列在图1。

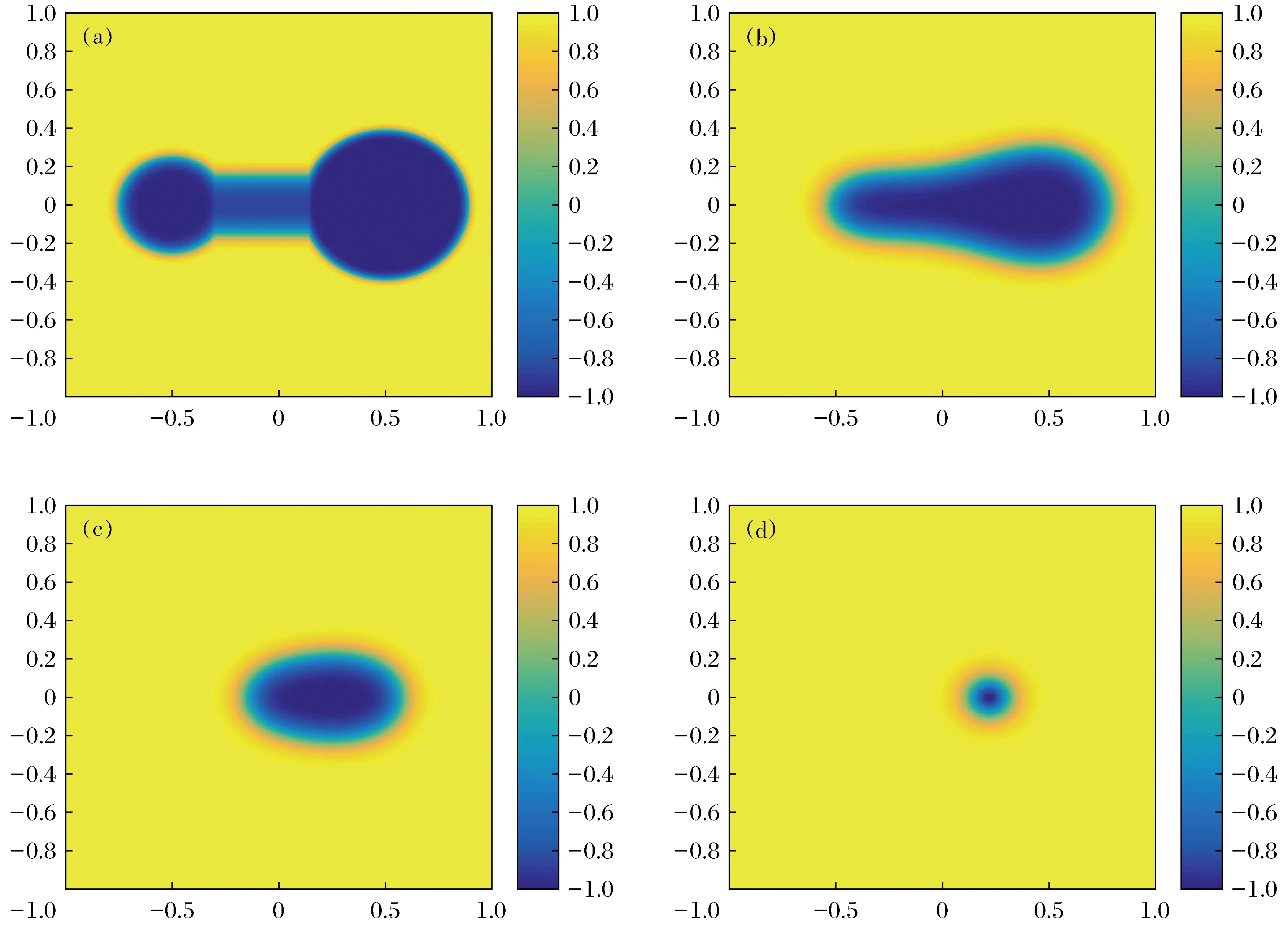
图1 算例在t=0,3.53×10-2,7.98×10-2,1.18×10-1时的数值解Fig.1 Numerical solution of the case t=0,3.53×10-2,7.98×10-2,1.18×10-1

图1显示了在不同时间点上Allen-Cahn方程解的数值结果。结果表明,随着时间增大,其形状由初始时间t0的哑铃状不断向圆形聚拢,数值结果与文献[11]中的结果吻合。

3 结 语

本文应用快速离散余弦变换结合积分因子方法求解非线性Allen-Cahn方程。该方法能够快速地将空间离散得到的非线性常微分方程组进行时间离散,得到方程的数值解,提高计算效率。通过求解齐次Neumann边界条件下的非线性Allen-Cahn方程,可以发现随时间推移数值结果形状的变化规律。

附录验证定理1中,Bxyj=λjyj,j=0,1,…,Nx-1,其中λj=2-2cos(jπ/Nx),yj=(cosjπξ1,…,cosjπξNx)T,j=0,1,…,Nx-1,由网格中心点的定义ξi=(i-1/2)h,i=1,2,…,Nx,在左右各增加一个虚拟网格,其中心点坐标为ξ0=-h/2,ξNx+1=1+h/2。

利用和差化积公式cos(jπξi-1)=cos(jπξi)cos(jπ/Nx)+sin(jπξi)sin(jπ/Nx)和cos(jπξi+1)=cos(jπξi)cos(jπ/Nx)-sin(jπξi)sin(jπ/Nx),可得-cos(jπξi-1)+2cos(jπξi)-cos(jπξi+1)=(2-2cos(jπ/Nx))cos(jπξi)。因为cos(jπξ0)=cos(jπξ1),cos(jπξNx)=cos(jπξNx+1),于是cos(jπξ1)-cos(jπξ2)=-cos(jπξ0)+2cos(jπξ1)-cos(jπξ2)=(2-2cos(jπ/Nx))cos(jπξ1),-cos(jπξNx-1)+cos(jπξNx)=-cos(jπξNx-1)+2cos(jπξNx)-cos(jπξNx+1)=(2-2cos(jπ/Nx))cos(jπξNx)。

验证完毕。