元素阶无平因子的有限群

何立国, 许聪儒, 皇甫莹

(沈阳工业大学, 理学院, 沈阳 110870)

0 引 言

一个自然数n如果不能被任意素数的平方整除,则称n是平方自由的,否则称之为非平方自由的。文献[1]研究了不可约特征标次都是平方自由的有限群G,证明了在G是不可解群时,若不计可解直因子,G同构于A7;在G是可解群时,G的导长和幂零长分别至多为4和3。文献[2]研究了关于共轭类长的类似结果,证明了若G的每个共轭类长都是平方自由的,则G是超可解的,且导长与幂零长分别至多为3和2。实际上在文献[1-2]中还提供了更加丰富的群结构信息。这种关于群的共轭长与不可约特征标次数之间出现对偶结果的现象引起了很多群论学者的兴趣[3-10],同时也引起了一个新问题:如将对群的关于特征标次数或共轭类长的约束条件替换为关于元阶的约束条件,即当群G的元素阶都是平方自由的情况下,G有什么样的结构呢? 本文证明了交错群An(n≥6),所有26个散在单群以及Tit单群中都是元素阶自由的。利用有限单群分类定理,进一步证明了若有限群G的每个子群与因子群均不同构于一个李型单群,则G是个可解群。此处视A5为一个李型单群, 这是因为A5≅PSL2(4)≅PSL2(5)。易见,群G是元阶平方自由的当且仅当G的方次数exp(G)是平方自由的。本文用N:H表示一个H作用在N的半直积,若G=N:H,则表示N是G的正规子群,G=NH且N∩H=1。

除非特别说明,本文的概念和术语都是标准的[11]。

1 引 理

引理1 如果G是元素阶平方自由的,则G的子群及因子群也是元素阶平方自由的。

引理2 交错群An(n≥6)不是元阶平方自由的,但A5是元阶平方自由的。

证明 交错群An(n≥6)包含一个元(1,2,3,4)(5,6),它的阶是4。应用GAP[4],可计算出A5的元阶集{1,2,3,5},故其是元阶平方自由的。

引理3 散在单群和Tit群2F4(2)′不是元阶自由的。

证明 通过逐一查文献[12]中的特征标表,可得26个散在单群中每一个均不是元阶自由的。 Tit群2F4(2)′包含阶是4的元,故也不是元阶平方自由的。证毕。

2 主要结果

定理1 设P是一个阶为pn的非交换群且exp(G)=p。那么G中存在k个元素x1,x2…,xk满足P=(…((Z(P)×〈xk〉):〈xk-1〉):…〈x2〉):〈x1〉,此处Z(P)表示P的中心且|P| =|Z(G)|p^k|。

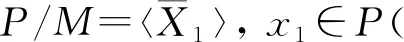
注意到即使在阶较小并且方次数exp(P)=p的情况下,一个p-群P也不一定是交换群。例如,利用GAP[13],可计算出阶为27的超特殊3-群刚好有2个,它们是 (C3×C3):C3和C9:C3。前一群的方次数是3,后一群的方次数是9。

定理2 设G是可解群且为阶平方自由的,那么G=(…(Pn:Pn-1):Pn-2):…P2):P1,满足任一Pi均为G的素数阶子群,1≤i≤n。

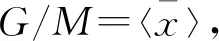
定理3 设G是元阶自由的且其子群和因子群均不同构于李型单群,则G是可解群。

证明 当G是交换群时,结果显然。如果G是非交换群,利用有限单群分类定理和引理2和3,可得G不是一个单群(此处将A5视作一个李型单群,这是因为A5≅PSL2(4)≅PSL2(5))。可以设N是G的一个非平凡正规子群,则由引理1得N和G/N均是元阶自由的。又因N和G/N的子群和因子群也是G的子群和因子群,所以也不同构于任一李型单群,由归纳法可得N和G/N是可解群,进而G是可解群。证毕。

定理4 非交换单群PSL2(pf),q=pf>3,当p=2,f≥3;或p>2,f≥2;或f=1,p>5,p-1和p+1之一能被8或r2整除(r是奇素数)时,包含非平方自由元素。当f=1,p>5并且p-1和p+1均为平方自由数时,它是元阶平方自由的。当f=1,p>5并且p-1和p+1之一有唯一平方因子4但不能被8整除时,它的元阶情况不确定。

证明 因为PSL2(4)≅PSL2(5)≅A5和PSL2(9)≅A6,所以由引理2可得PSL2(4)和PSL2(5)是元阶平方自由的,但PSL2(9)不是元阶平方自由的。

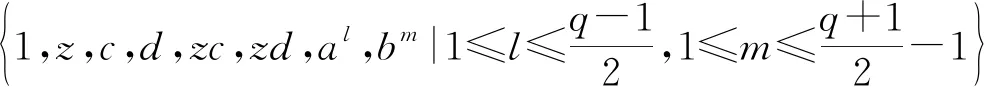
因为(p+1,p-1)=2,故如果4整除p-1时,那么4不整除p+1;反之亦然。因此当提及4整除p-1,p+1时,实际上4至多整除其中之一,不会出现同时整除的情况。利用GAP[5],可以计算出PSL2(13)的元阶集是{1,2,3,6,7,13}和PSL2(53)的元阶集等于{1,2,3,9,13, 26,27,53}。可见前一群PSL2(13)是元阶平方自由的,而后者PSL2(53)是非元阶平方自由的,它有能被9整除的元阶。易见13-1=22*353-1 =22*13均是只含平方因子4的数。也可得PSL2(11)的元阶集是{1,2,3,5,6,11}和PSL2(19)的元阶集等于{1,2,3,5,9,10,19}。可见前一群PSL2(11)是元阶平方自由的,而后者PSL2(19)是非元阶平方自由的,它有9阶元。易见 11+1=22*3和19+1=22*5均是只含平方因子4的数。证毕。

易见阶为1，2，3的群都是平方自由的，阶为4的群刚好一个是平方自由的,即C2×C2。

利用GAP可以算出阶至多为50的平方自由群共有84个同构类，它的结构及元阶集如下:

在下面第一组数据中,数据(5,1),C5,[1, 5]中的(5,1)表示小群 G=SmallGroup(5,1),C5表示StructureDescription(G),[1, 5]表示G的阶集。

(5,1),C5,[1, 5];(6,1),S3,[1, 2, 3];(6,2),C6,[1, 2, 3, 6];(7,1),C7,[ 1, 7];(8,5),C2×C2×C2,[1, 2];(9,2),C3×C3,[1, 3];(10,1),D10,[1, 2, 5];

(10,2),C10,[1, 2, 5, 10];(11,1),C11,[1, 11];(12,3),A4,[1, 2, 3];

(12,4),D12,[1, 2, 3, 6];(12,5),C6×C2,[1, 2, 3, 6];(13,1),C13,[1, 13];(14,1),D14,[1, 2, 7];(14,2),C14,[1, 2, 7, 14];(15,1),C15,[1, 3, 5, 15];

(16,14),C2×C2×C2×C2,[1, 2];(17,1),C17,[1, 17];

(18,3),C3×S3,[1, 2, 3, 6];(18,4),(C3×C3) : C2,[1, 2, 3];

(18,5),C6×C3,[1, 2, 3, 6];(19,1),C19,[1, 19];(20,4),D20,[1, 2, 5, 10];

(20,5),C10×C2,[1, 2, 5, 10];(21,1),C7 : C3,[1, 3, 7];(21,2),C21,[1, 3, 7, 21];(22,1),D22,[1, 2, 11];(22,2),C22,[1, 2, 11, 22];(23,1),C23,[1, 23];

(24,13),C2×A4,[1, 2, 3, 6];(24,14),C2×C2×S3,[1, 2, 3, 6];

(24,15),C6×C2×C2,[1, 2, 3, 6];(25,2),C5×C5,[1, 5];(26,1),D26,[1, 2, 13];

(26,2),C26,[1, 2, 13, 26];(27,3),(C3×C3):C3,[1, 3];(27,5),C3×C3×C3,[1, 3];

(28,3),D28,[1, 2, 7, 14];(28,4),C14×C2,[1, 2, 7, 14];(29,1),C29,[1, 29];

(30,1),C5×S3,[1, 2, 3, 5, 10, 15];(30,2),C3×D10,[1, 2, 3, 5, 6, 15];

(30,3),D30,[1, 2, 3, 5, 15];(30,4),C30,[1, 2, 3, 5, 6, 10, 15, 30];

(31,1),C31,[1, 31];(32,51),C2×C2×C2×C2×C2,[1, 2];(33,1),C33,[1,3,11, 33];

(34,1),D34,[1, 2, 17];(34,2),C34,[1, 2, 17, 34];(35,1),C35,[1, 5, 7, 35];

(36,10),S3×S3,[1, 2, 3, 6];(36,11),C3×A4,[1, 2, 3, 6];

(36,12),C6×S3,[1, 2, 3, 6];(36,13),C2×((C3×C3) : C2),[1, 2, 3, 6];

(36,14),C6×C6,[1, 2, 3, 6];(37,1),C37,[1, 37];(38,1),D38,[1, 2, 19];

(38,2),C38,[1, 2, 19, 38];(39,1),C13 : C3,[1, 3, 13];(39,2),C39,[1, 3, 13, 39];

(40,13),C2×C2×D10,[1, 2, 5, 10];(40,14),C10×C2×C2,[1, 2, 5, 10];

(41,1),C41,[1, 41];(42,1),(C7 : C3) : C2,[1, 2, 3, 6, 7];

(42,2),C2×(C7 : C3),[1, 2, 3, 6, 7, 14];(42,3),C7×S3,[1, 2, 3, 7, 14, 21];

(42,4),C3×D14,[1, 2, 3, 6, 7, 21];(42,5),D42,[1, 2, 3, 7, 21];

(42,6),C42,[1, 2, 3, 6, 7, 14, 21, 42];(43,1),C43,[1, 43];

(44,3),D44,[1, 2, 11, 22];(44,4),C22×C2,[1, 2, 11, 22];

(45,2),C15×C3,[1, 3, 5, 15];(46,1),D46,[1, 2, 23];(46,2),C46,[1, 2, 23, 46];(47,1),C47,[1, 47];(48,49),C2×C2×A4,[1, 2, 3, 6];

(48,50),(C2×C2×C2×C2) : C3,[1, 2, 3];(48,51),C2×C2×C2×S3,[1, 2, 3, 6];

(48,52),C6×C2×C2×C2,[1, 2, 3, 6];(49,2),C7×C7,[1, 7];

(50,3),C5×D10,[1, 2, 5, 10];(50,4),(C5×C5) : C2,[1, 2, 5];

(50,5),C10×C5,[1, 2, 5, 10];

通过分析上面数据可得下面结果:

定理5 设G阶至多为50阶的平方自由群,那么G刚好有84个同构类且全可解群,并且刚好有47个同构类是幂零群。

通过进一步分析由GAP计算的数据可得2 000阶以内平方自由群的结构,简述如下:

定理6 设G阶不超过500阶的平方自由群,那么G刚好有1 570个同构类, 其中可解群有1 561个同构类,幂零群有527个同构类。

可见500阶以内的平方自由群中非可解群共有9个同构类,利用GAP可算得它们分别是SmallGroup(60,5),SmallGroup(120,35),SmallGroup(180,19),SmallGroup(240,190), SmallGroup(300,22),SmallGroup(360,121),SmallGroup(360,122),SmallGroup(420,13),SmallGroup(480,1 187)。并且可得它们分别同构于A5,C2×A5,GL(2,4),C2×C2×A5,C5×A5,A5×S3,C6×A5,C7×A5,C2×C2×C2×A5。