RS、ZB、CsCl结构的XC(X=Mg、Ca、Sr、Ba)第一性原理计算

封文江, 谢金峰, 高 雅, 徐乾浩, 刘 岩, 赵雪桐

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)

碱土金属化合物是自旋电子学的重要研究对象之一,与传统电子学不同,它既利用电子的电荷属性,同时也把电子的自旋作为信息的载体,来更高效地对信息进行处理和存储,目前已普遍应用于通信、信息存储、工业等领域中,具有重要的科研价值[1]。

2004年, Kusakabe等计算了ZB结构下的CaAs,其能带结构图中表明具有半金属性,总磁矩为2 μB。之后人们又发现了半金属性在ZB结构IIA-IVA、IA-VA[2]及IA-IVA[3]化合物中存在。传统的半金属材料中主要由过渡金属的d电子贡献其半金属性的形成,同时一般也都表现为铁磁性,但是在ZB结构的碱(碱土)金属IVA、VA族化合物中,没有过渡金属等磁性原子的存在,因此主要是由IVA、VA族元素的p电子贡献其半金属铁磁性。本文利用密度泛函理论的第一性原理方法,计算了碱土金属与C原子化合物的磁学性能与力学性能,并依靠分析计算所得数据得出合理的结论。

1 计算方法

对材料分析的理论方法是基于量子力学密度泛函理论的第一性原理。Materials Studio6.0的CASTEP模块是基于赝势平面波用于计算与电子交换相关能,考虑到电子密度的不均匀性采用广义梯度算法(GGA)来模拟计算XC(X=Mg、Ca、Sr、Ba)化合物的磁学性能与力学性能。为了使总能量更好地收敛,对4种化合物的3种不同结构的初次优化设置的参数为:布里渊区k点值设置6×6×6,截断能为310 eV,总能收敛精度设为1×10-6eV。

2 结果与讨论

2.1 晶体结构

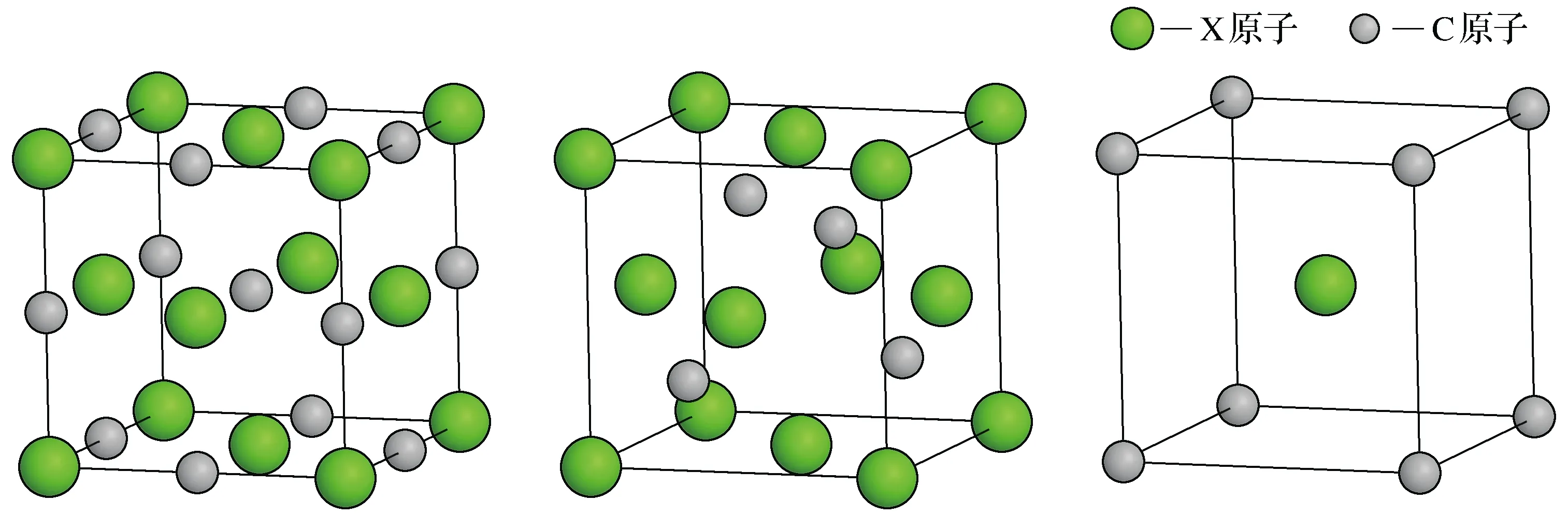
图1 XC的晶体结构Fig.1 Crystal structure of XC

2.2 基态性质与磁性

图2中分别表示XC在3种不同结构(RS、ZB、CsCl)下改变晶格常数时得到的结构最低能量。

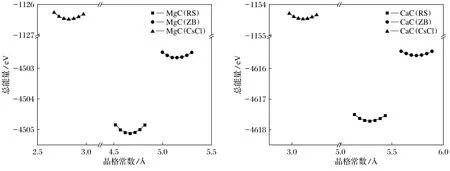
图2 在RS、ZB、CsCl结构下变化晶格常数的自旋极化总能量Fig.2 Total energy of spin polarization changing lattice constants in RS,ZB,CSCL structures

从图2中可以看到,对于MgC和CaC这2种化合物,ZB结构在单晶胞能量上相比其他结构最不稳定,而岩盐结构是稳定的。表1为MgC和CaC的优化平衡晶格常数,分别为4.665和5.284 Å。BaC和SrC已有研究表明在RS结构最稳定,SrC和BaC都表现出半金属铁磁体特性,整数磁矩为2.00 μB/f.u[4]。在RS结构的平衡体积上,MgC和CaC计算得到的总磁矩大小分别为0.94 μB和1.98 μB。在每个原子的自旋磁矩中经分析得出,对总磁矩贡献最大的是C原子,MgC与CaC中C的磁矩贡献分别约占总磁矩的78.7%和73.7%。因此,XC在岩盐结构下的磁性贡献均主要来源于C-2p电子的能级劈裂。此外,还可以看出CaC表现出近半金属铁磁体特性,MgC表现出金属铁磁体特性但CsCl型结构中都没有自旋极化。因此,主要研究了具有稳定RS结构的MgC和CaC的磁学性质。

表1 总磁矩和各原子磁矩实验值Table 1 Total magnetic moment and experimental values of each atom magnetic moment

2.3 能带结构

图3与图4分别为将Mg、Ca与C原子设置自旋向上的CaC和MgC的能带结构图。

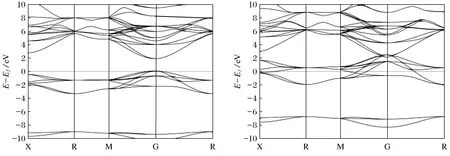
图3 CaC能带结构图Fig.3 Energy band structure of CaC

其中图3左侧为Ca、C原子都自旋向上,可以观察到自旋向上能带结构在费米面与价带顶基本相切并与导带底之间存在着约2 eV的明显带隙,证实结构体现出半导体性质;图3右为自旋向下的能带结构图,在该图中发现费米面在能带穿过,且存在重叠部分,从而显示出金属性质。CaC能带结构图符合近半金属材料能带结构的特点,所以从能带结构图分析CaC具有近半金属性[7]。

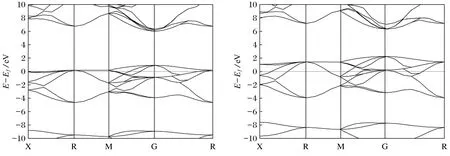
图4 MgC能带结构图Fig.4 Energy band structure of MgC

图4的MgC能带图同理, 可以观察到自旋2个方向的能带均穿过了费米面, 即说明导带和价带之间发生重叠, 在自旋向上方向的能带结构图中费米面以上存在着约5 eV的明显带隙, 在自旋向下方向的能带结构图中,费米面以上存在着约4 eV的明显带隙, 所以从能带结构图分析出MgC表现为金属性质。

2.4 态密度

图5显示了岩盐结构下CaC和MgC在其平衡晶格常数下的总态密度图和原子自旋态密度主要部分对比图。这里,只给出C(p)和Ca(Mg)d态的部分态密度,因为费米能级周围的其他态的值很小。从总态密度可以看出,很明显原子磁矩主要来源于C原子而Mg、Ca原子对其贡献很小。在图5中C(p)轨道态密度图2个自旋方向的峰值在费米能级附近基本对称,所以明显看出C原子的能级劈裂,即岩盐结构下的这几种化合物磁性主要来源于C原子。这一结果和2.2中对磁矩的分析结果一致。这里BaC和SrC在岩盐结构下表现出与MgC和CaC相同的性质,原子磁矩主要来源于C原子而Ba、Sr原子对其贡献很小。这表明了XC在岩盐结构下的磁性贡献均主要来源于C原子[8]。

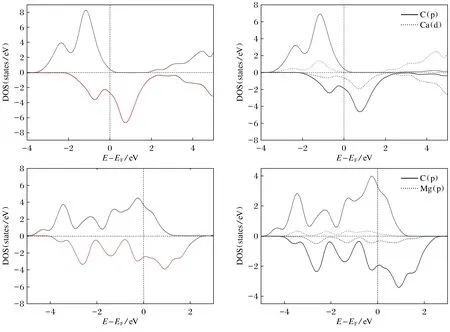
图5 在平衡晶格常数下,岩盐结构CaC(上图)和MgC(下图)的自旋总态密度和部分轨道态密度Fig.5 Spin-resolved tota and partial densities of states for RS CaC(up) and MgC(dn) at equilibrium lattice constants

2.5 力学性质

在晶格常数最优化的基础上,使用GGA计算XC(X=Mg、Ca、Sr、Ba)在零压下的弹性常数来反映材料的稳定性、延展性、硬度、脆性等等。弹性常数的物理意义是:晶体对外力的反应程度由体积模量B、Voigt剪切模量GV、Reus剪切模量GR、杨氏模量Y和泊松比υ几种参数来表征。在对材料研究的过程中,因为结构具有对称性,弹性模量矩阵参数Cij,i,j=1,2,3,4,5,6中有3个独立参数,分别为C11、C12和C44,其中C11和C12是用来反映晶体对单向压缩的变化量,C44正比于剪切模量,所以可以用来测量剪切形变值[9]。上述参数的计算公式分别为

表2为岩盐结构下的4种材料采用上述公式进行计算得出的数据。对于立方晶格来说,满足传统力学稳定性的条件为C11>0,C44>0,C11-C12>0,C11+2C12>0和C12

在表格中通过上述条件可以发现CaC与BaC作为晶体具有良好的力学稳定性[10]。

金属材料的力学性能一般由延展性和塑性来表征,根据Pugh理论[11],用B/G的值来反应材料的延展性与脆性,它的临界值为1.75,B/G值越大延展性越好。表中CaC的B/G值为4.23,BaC的B/G值为3.07,表明这2种材料是拥有良好延展性的材料。根据Frantsevich法则,可以通过材料的泊松比υ来判断材料的脆性和延展性。当υ>0.26时说明材料是易延展性的材料,否则说明为脆性材料[12]。观察结果可以看出,CaC与BaC这2种材料的泊松比都满足大于0.26,表明其为易延展材料。综上所述,说明CaC与BaC是2种具有延展性的材料。

表2 岩盐结构下XC(X=Mg、Ca、Sr、Ba)力学计算参数Table 2 Mechanical calculation parameters of XC (X=Mg,Ca,Sr,Ba) in rocksalt structure

3 结 论

本文对比了岩盐结构下XC(X=Mg、Ca、Sr、Ba)材料的磁学性能与力学性能。材料的电子性能部分,在2.2节中列出了MgC和CaC的3种结构总能量变化图,说明2种材料均在岩盐结构下是稳定的,进而研究了在此结构下的各化合物的能带结构、总磁矩与原子磁矩。在能带结构中,发现CaC为近半金属铁磁体,MgC为金属铁磁体。在RS结构的平衡体积上,MgC和CaC计算得到的总磁矩大小分别为0.94 μB和1.98 μB,在XC的态密度及各原子态密度的计算结果中,发现XC的磁性主要来源于C-2p电子的能级劈裂。力学性能部分,发现CaC与BaC是良好的易延展性材料。