非局域MKdV方程平面波背景下的精确解

于发军, 刘苡妍, 李 丽

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

0 引 言

最近,Ablowitz和Musslimani[1-2]提出了一些新的非局部可积非线性方程,包括非局部可积非线性薛定谔方程、MKdV方程等。根据波的相对长度与介质非线性响应函数的相对尺度,非局部非线性方程可分为4类:局部类[3]、弱非局部类、一般非局部类和强非局部类。非局域非线性介质中的空间孤子引起了人们极大的兴趣[4-6],其中文献[7]介绍了非局域空间孤子的研究现状。

随着孤子理论研究的深入,出现了求解非线性偏微分方程的许多方法,如齐次平衡法[8]、双线性[9]、Darboux变换(DT)法[10]、反散射变换法[11-13]。文献[14]中推导出Ablowitz-Musslimani方程的具有等时对称势的一些离散的畸形波解。Li和Xu在文献[17]中通过N次Darboux变换,得到了具有自诱导拟时对称势的非局部NLS方程的局域波解。利用广义达布变换,文献[18]导出了具有散焦型非线性的对称非局部NLS模型的有理孤子解,包括1-阶解、暗-反暗孤子和反暗-暗孤子。Zhang,Qiu,Cheng和He推导了一类非局部NLS方程的带有2个自由相位参数的有理解,该解满足文献[19]中的等时(PT)对称性条件。闫等在文献[20]中提出了连续可积局部和非局部向量NLS方程统一的双参数波模型。

对于可积孤子方程,构造显式解一直是一个基本而重要的问题。然而,目前对于反时空非局部MKdV方程的研究工作较少。本文对非局域MKdV方程构造N次DT,求反时空MKdV方程的精确解,主要从平面波背景推导出了一些单孤子、双孤子和N孤子解公式。

1 Darboux变换求解非局部MKdV方程

最近文献[1-2]中给出了一个可积实非局部(也称反时-空)MKdV方程

Qt(x,t)-6σQ(x,t)Q(-x,-t)Qx(x,t)+Qxxx(x,t)=0

(1)

这里:σ=1表示聚焦情况;函数Q(x,t)是实函数。该方程可以描述非线性海洋大气动力系统[21]中非局域MKdV方程的一般形式。方程(1)的Lax对可以用以下形式表示:

这里:Q(x,t)和Q(-x,-t)是x和t的势函数;λ是一个谱参数;φ=(φ1,φ2)T是方程(2)和(3)的列向量解与特征值λ有关,并且i2=-1。

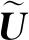
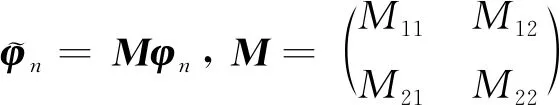
(4)

利用兼容性获得如下形式:

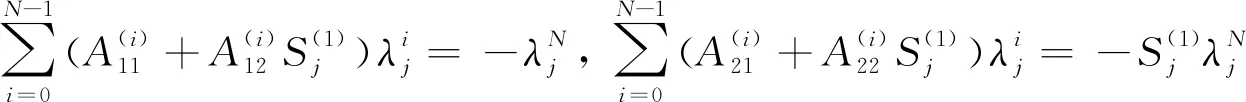
(7)

其中

(8)

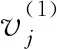
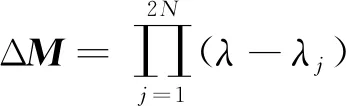
(10)

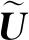
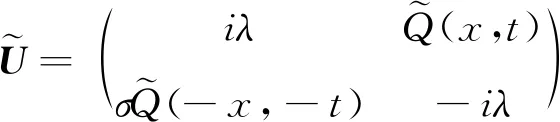
(11)

下式给出DT变换下新解和旧解的关系:

(12)

在这里式(12)是通过方程(5)的达布变换得到的。

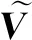
2 平面波背景下非局域MKdV方程的N-孤子解

为了得出方程(1)的N-孤子解表达式,考虑矩阵M如下:

根据方程(15)和克莱姆法则,得到

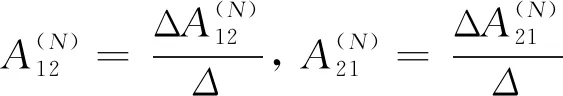
(16)

其中

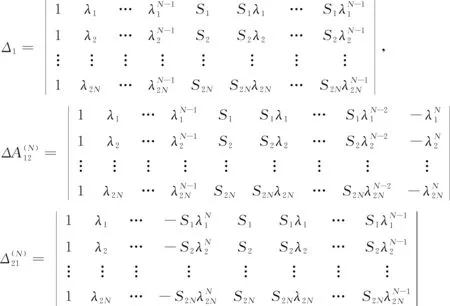
(17)

基于方程(4),(12)和(17),可以推导出MKdV方程N-孤子解的新公式如下:

(18)

在方程(18)中,分别考虑N=1,2并将其结构绘制为图1和图2。在这一节中,将利用N次DT给出方程(1)的一些新的精确解。首先给出种子解Q(x,t)=Aeαx,其次将其代入方程(2)和(3),可得到上述方程的2个基本解:

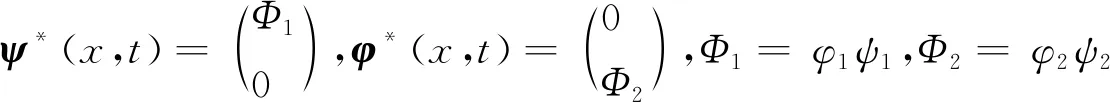
(19)

图1 1-孤子解的密度图

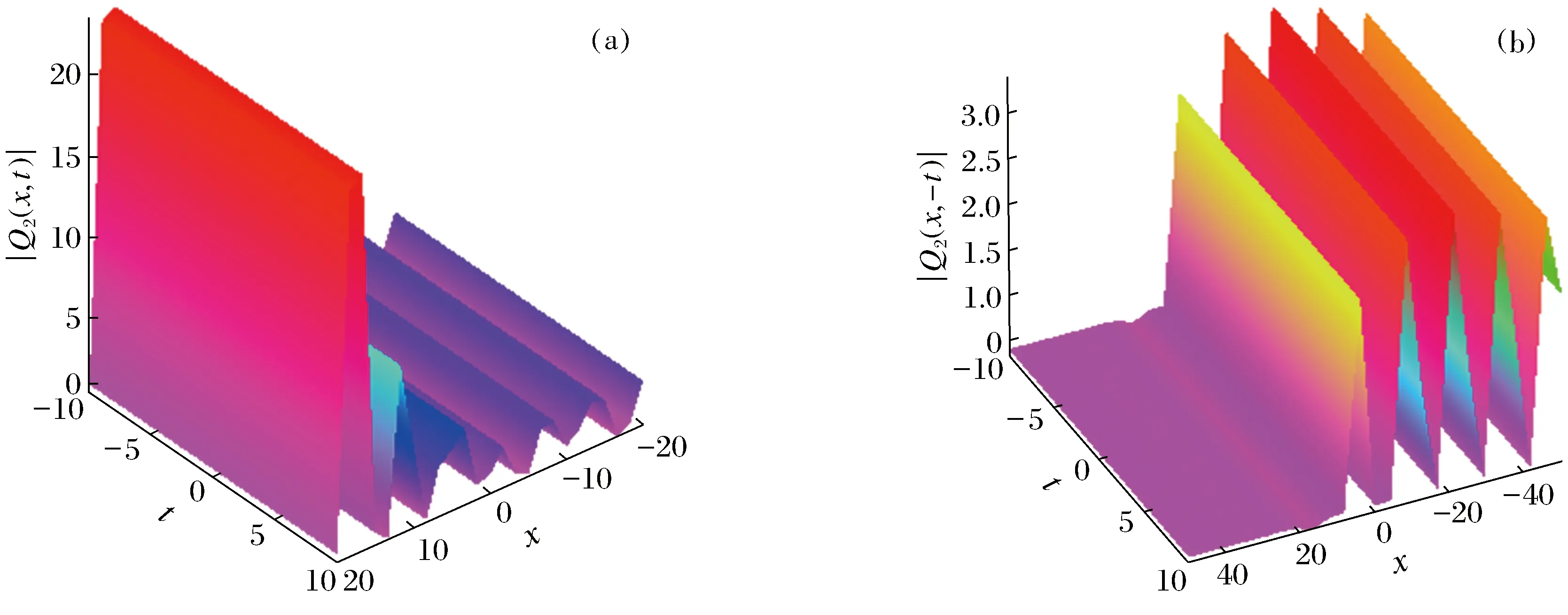
图2 2-孤子解的密度图

其中

利用等式(8)和(19),得到Sj如下:

(20)

为了获得方程(1)的解,分别考虑N=1,2的情形。

1) 考虑N=1,且有λ=λj(j=1,2),求解方程(7)可得

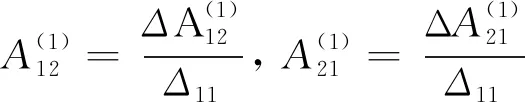
(21)

其中

(22)

根据DT,得到具有平面波背景的非局域MKdV方程(1)的非局域单孤子解如下:

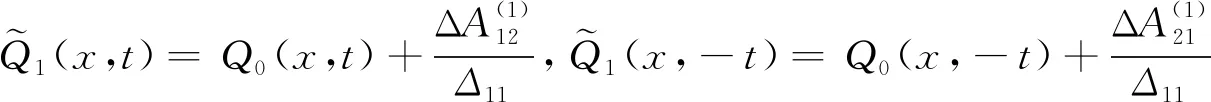
(23)

2) 考虑N=2,且有λ=λj(j=1,2,3,4),求解方程(7)可得

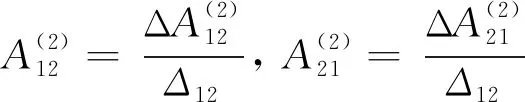
(24)

其中

通过DT公式得到非局域MKdV方程(1)的非局域2-孤子解:

(25)

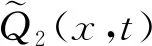
3 结 论

本文构造了非局部MKdV方程的DT。通过选取合适的参数,给出了具有平面波背景的N-孤子解的表达式。通过求解MKdV方程,发现它与非线性局部MKdV方程的解有很大的不同。此外,还研究了这些解的动力学行为。这些结果有助于理解一些物理现象。该方法也适用于物理和数学中更多的非线性非局部孤子方程。