CNSBS曲面拼接方法的设计与实现

吴丽娟, 张心慈, 任海清, 梁岱立, 黄 尧, 齐维毅

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)

B样条的概念最初是由Schoenberg于20世纪40年代中提出来的[1-4],60年代末70年代初,Riesenfeld,Coons和Clark等的论著取得了最初的成果;其后10年间,各国学者如Wu,Abel和Greenberg,朱心雄和吴瑞祥等也发表了论文与著作[5-7],对B样条方法进行了更为广泛的研究。

当用B样条曲面构造i阶(i=1,2,…,n)连续的4边曲面或N边曲面时,要求被插值的跨界导矢之间必须满足一定的约束条件,跨界导矢不能独立地给出,约束条件难以满足[8-10],而Coons曲面是由已知的边界曲线生成的。

因此,我们将Coons曲面的构造原理与B样条曲线相结合,构造了一种新的曲面,称为Coons类混合B样条曲面,简称CNSBS曲面。本文根据边界曲线和跨界导矢构造过渡的CNSBS曲面。结果显示,该曲面与周边B样条曲面处处C1连续。

1 曲面定义

1.1 B样条曲线与曲面

1) B样条曲线方程定义为

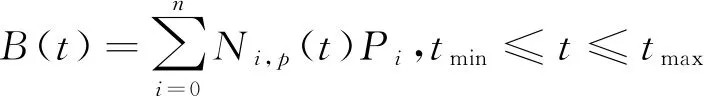
(1)

图1 B样条曲线Fig.1 B-spline curve

式中:Pi是B样条曲线的控制顶点;Ni,p(t)是定义在节点空间上的p次B样条基函数。根据控制顶点生成的B样条曲线如图1所示。

2) 由B样条曲线的定义,可得到B样条曲面的定义如下:

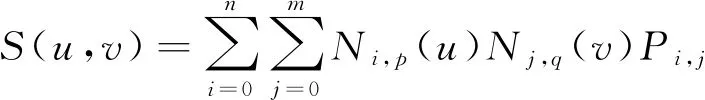
(2)

定义中Pi,j(i=0,1,…,n;j=0,1,…,m)是B样条曲面的控制顶点;Ni,p(u)和Nj,q(v)是B样条基函数。构建的B样条曲面如图2所示。

图2 B样条曲面Fig.2 B-spline surface

1.2 Coons曲面

已知Coons曲面的4条边界曲线分别为P(u,0),P(u,1),P(0,w)和P(1,w),曲面的4个角点分别为P(0,0),P(0,1),P(1,0)和P(1,1)[11]。则插值这4条边界的Coons曲面的表达式为

Q(u,w)=Q1(u,w)+Q2(u,w)-Q3(u,w)

(3)

式中

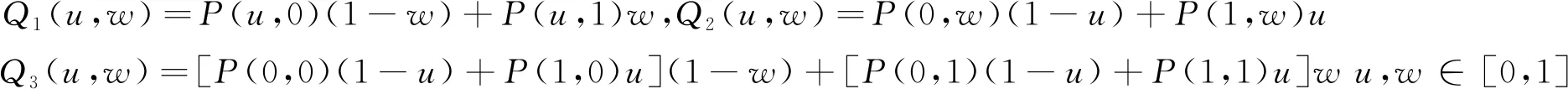
(4)

2 B样条曲面的拼接

2.1 设计流程

给定控制点,生成4片待拼接的B样条曲面;根据边界曲线上的型值点,运用反算算法求出控制点,生成4条边界曲线,并求出其跨界导矢;运用节点插入算法,求出待生成曲面上的控制顶点;根据求出的控制顶点和基函数生成2个B样条曲面,并求出表达式;将2张曲面合并成1张曲面,得到拼接后的过渡CNSBS曲面。

2.2 实现过程

2.2.1 构建边界曲线

已知型值点Pi(i=1,2,…,n),求出控制点Vj(j=1,2,…,n+1,n+2)[12]。具体过程如下:

3次均匀B样条曲线的矩阵形式为

(5)

根据(5)式可以列出n个求解B样条曲线控制点的方程组:

(6)

因为所求的控制点个数为(n+2),所以要再补充2个端点条件:

首端切矢

(7)

末端切矢

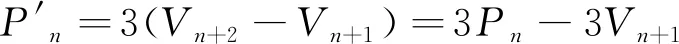
(8)

求解(6)式～(8)式即可得到全部待求控制点Vj。

根据(1)式B样条曲线定义可得边界曲线:

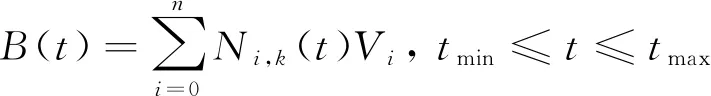
(9)

2.2.2 求跨界导矢

要使过渡曲面与待拼接曲面处处C1连续,关键是对边界B样条曲线的基函数求导:

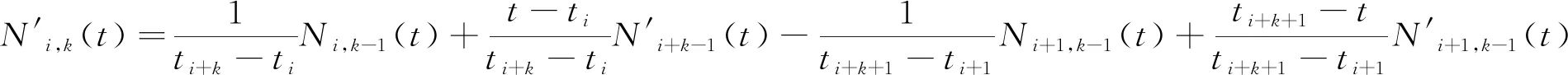
(10)

因此可以得到边界曲线的跨界导矢:

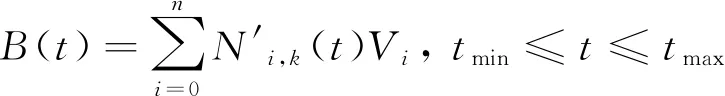
(11)

2.2.3 插入节点

设k次B样条曲线的控制顶点为P=[P0,P1,…,Pn],在节点区间[ui,ui+1]内插入节点u。

根据节点插入算法:

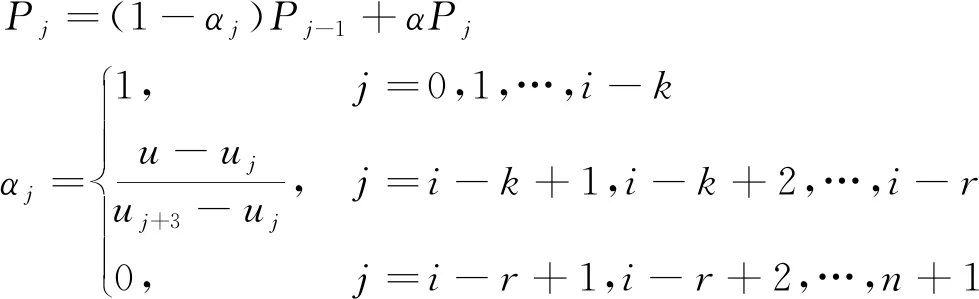
(12)

其中k=3,r为所插入节点的重复度,令r=0;由此可以求出插值于边界曲线的过渡曲面的控制顶点Pij和Qij[13-14]。

2.2.4 构建B样条曲面

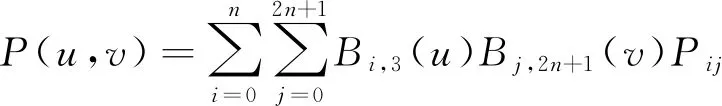
(13)

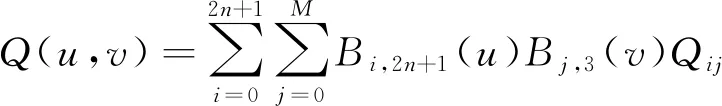
(14)

式中:Bi,3(u)(Bj,3(v)),Bj,2n+1(v)Bi,2n+1(u)是B样条基函数;Pij(i=0,1,…,N,j=0,1,…,2n+1)Qij(i=0,1,…,2n+1,j=0,1,…,M)是B样条曲面P(u,v)Q(u,v)的控制顶点;(N+1)(或(M+1))是控制顶点数[15]。

2.2.5 构造拼接曲面

将2张B样条曲面合并成1张CNSBS曲面,由于2张曲面不能直接相加,需要求出2片曲面所占权重,并满足约束条件:

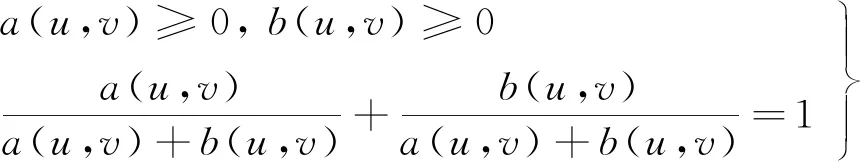
(15)

根据Coons曲面的生成原理,得到插值于4条边界线及其跨界导矢的CNSBS曲面的表达式为

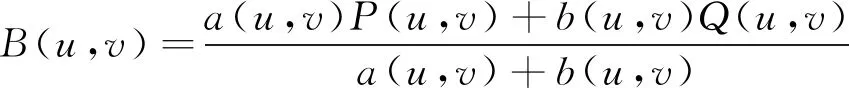
(16)

式中a(u,v)=un+1(1-u)n+1,b(u,v)=vn+1(1-v)n+1,(1-u),u,(1-w)和w都是Coons曲面的线性函数。

得到的待拼接曲面和拼接后的曲面如图3和图4所示。

图3 待拼接的B样条曲面Fig.3 B-spline surfaces to be spliced

图4 拼接后的曲面Fig.4 Surface after splicing

3 结 论

通过上述算法设计与实现过程可知,根据4条边界曲线及其跨界导矢构造过渡曲面的方法,拼接得更加精准,运用C++语言和OpenGL函数进行编程操作,在Visual Studio 2010平台上进行调试,最终生成的CNSBS曲面整体C1连续。运用此方法拼接的曲面无需满足跨界导矢之间的约束条件,并且同样具有B样条曲面的性质,可以实现曲面形状的控制。