用等效DBHF方法计算分析重核性质

刘 玲, 张 宽

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)

0 引 言

原子核基态性质一直是核物理领域最基本的研究问题之一,重核的性质又是人们尤为感兴趣的热点问题,重核的核外电子数较大,核外电子运动速度很快,相对论效应就变得非常重要。其理论研究不仅在原子核结构方面有重要意义,对重核裂变、超重核的合成[1-2]等方面也有着重大的作用。

相对论平均场理论(RMF)[3-7]和Dirac Brueckner Hartree-Fock(DBHF)方法[8]在描述核性质方面都取得了很大的成功。线性相对论平均场理论给出的不可压缩系数过大,为此,引入了非线性自相互作用[9-12],但是同时增加了模型的可调参数,人们通过调节核物质不可压缩系数及大量稳定核的性质,如结合能、电荷均方根半径等,来确定这些参数。目前有很多比较成功的参数,如NL1[10]、NL-SH[11]、NL3[12]等。非线性平均场理论非常成功地描述了大量核的基态性质,但其中存在自由的可调参数,虽然各套参数能够给出一致的稳定核性质,但推广到滴线核或超重核时,却给出了不同的结果。DBHF方法是直接从自由的核子-核子相互作用出发的相对论微观理论,它成功地描述了核物质饱和性质的经验值,但计算难度相当大,很难对有限核的性质进行计算。

Brockmann和Toki[13]发展了密度依赖的相对论平均场方法,即等效DBHF方法。在该方法中,介子的耦合常数不再是通过符合核物质饱和点性质来调节的常数,而是随着核子密度、同位旋变化,在每个密度处和不同的同位旋状态下,使相对论平均场与DBHF这2种方法中得到的自能相一致,从而确定每个密度点处以及不同的同位旋状态下,介子在相对论平均场下的耦合常数,将密度依赖性与同位旋依赖性引入到了拉格朗日密度当中。这样密度、同位旋依赖的耦合常数不是自由参数,它们不是通过唯象拟合任何核多体问题数据来得到的。既没有自由的可调参数,又保留了直接从微观核子-核子相互作用出发。将此方法推广到研究远离β稳定线核的性质时,所得结果更具有说服力,理论有效性更强。

1 理论方法

将核子描述为通过交换多种介子相互作用的系统,考虑σ、ω、ρ、δ介子以及γ光子的作用,从有效Lagrangian密度[14-15]出发,

利用Euler-Lagrange公式,可以求出介子场满足的运动方程。在相对论平均场近似下,将介子场算符用他们的基态期望值代替,介子场方程退化为Klein-Gordon方程形式:

同理,求得核子场的Dirac方程:

从动量张量出发,系统的总能量可表示为

其中:ρS(r)为标量密度;ρB(r)为矢量密度,

原子核的中子均方根半径、质子均方根半径、电荷均方根半径分别为

在等效DBHF方法中,介子的耦合常数随着核子密度、同位旋变化,在每个密度处和不同的同位旋状态下,使相对论平均场与DBHF这2种方法中得到的自能相一致,从而确定每个密度点处以及不同的同位旋状态下,介子在相对论平均场下的耦合常数,将密度依赖性与同位旋依赖性引入到拉格朗日密度当中。这样密度、同位旋依赖的耦合常数不是自由参数,它们不是通过唯象拟合任何核多体问题数据来得到的。有效介子密度、同位旋依赖的耦合常数为

其中α表示不对称系数,密度、同位旋依赖的耦合常数在相对论平均场中等效地包含了核子的短程关联效应及DBHF同位旋结构。

2 结果和讨论

经过计算分析,得到206-211Bi、219-224Rn、224-229Ac等同位素链的核性质。以219-224Rn为例,将利用等效DBHF方法计算得到每粒子结合能与权威的评价数据[16-17]进行比较,如图1所示。

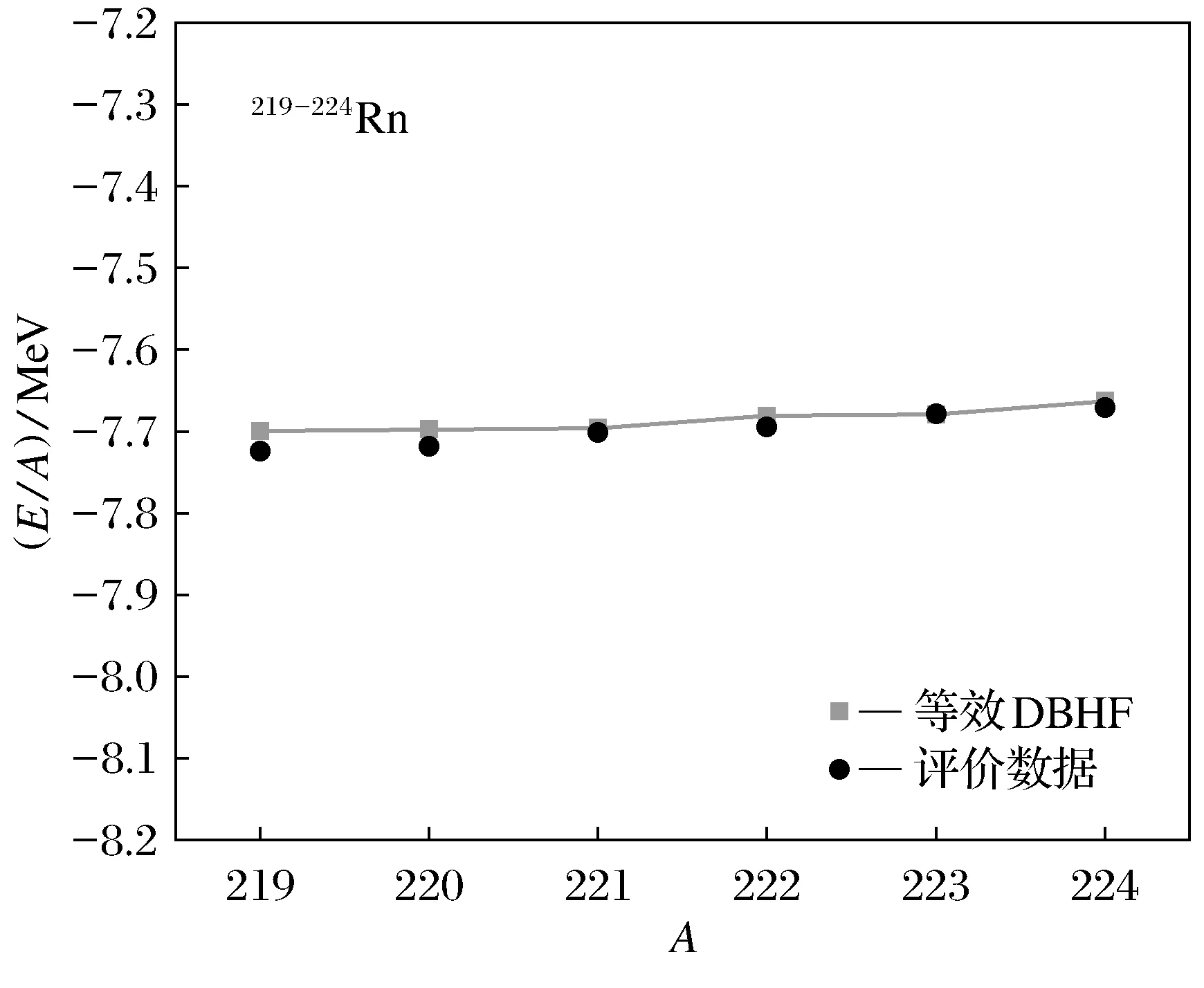
图1 同位素链每粒子结合能Fig.1 Isotopic chain binding energy per particle

由图1可以知道,等效DBHF方法计算得到的219-224Rn同位素链的每粒子结合能与评价数据符合度很好,差值在0.000 1～0.01 MeV。将每组同位素链中计算结果与评价数据符合度最好的粒子单独列出,如图2所示。

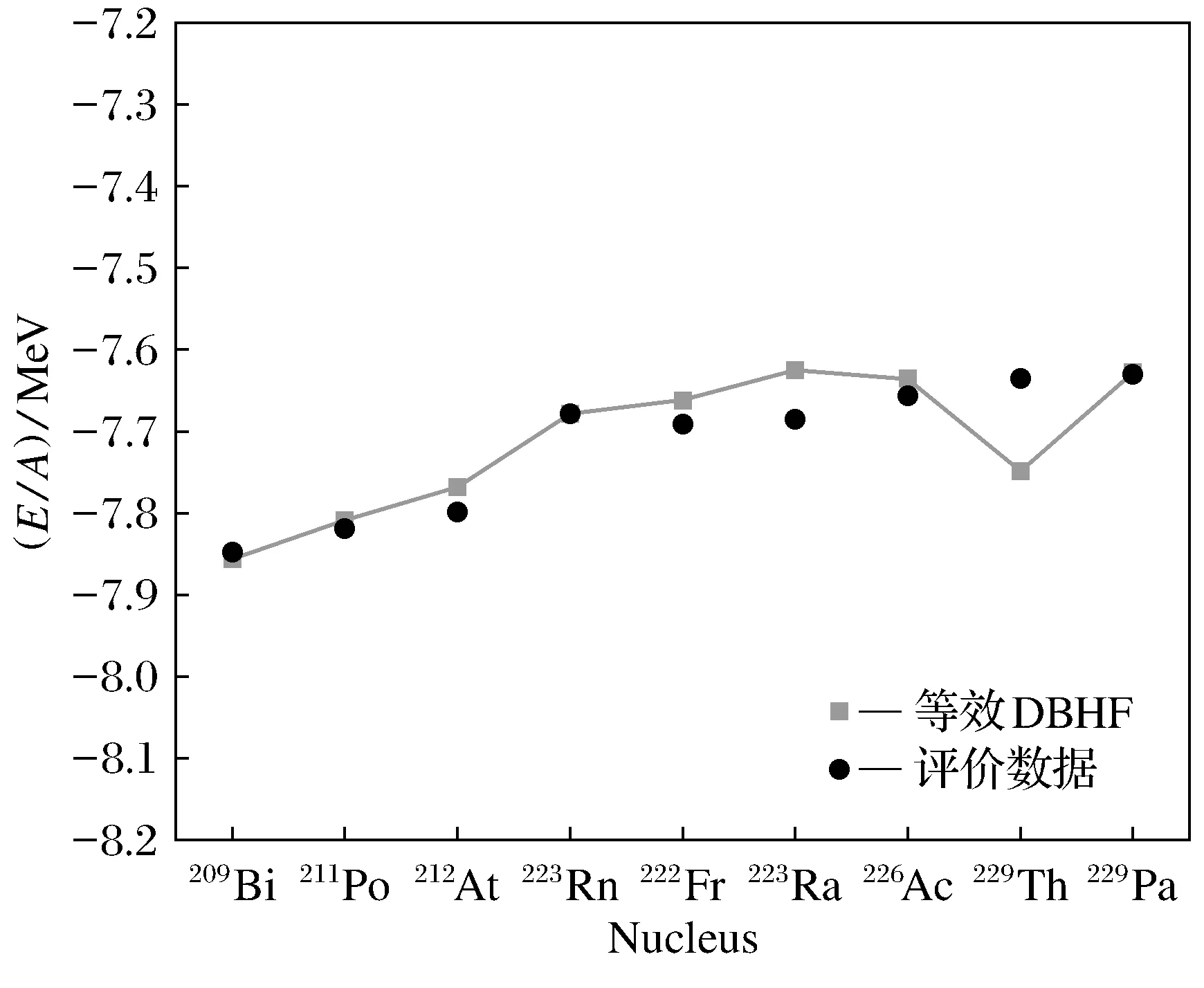
图2 符合度最好的每粒子结合能

由图2可以知道,各同位素链中符合度最好的粒子,每粒子结合能的计算结果与评价数据之间的差值在0.000 1～0.1 MeV。其中223Ra、229Th的误差较大,产生这种现象可能是因为未能全面考虑原子核结构效应,如壳效应等,导致一些性质规律发生变化。

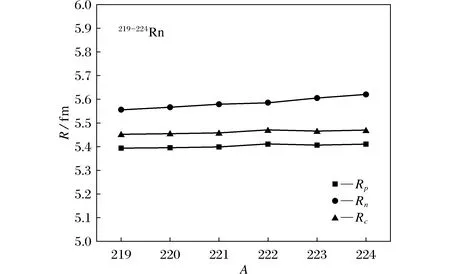
图3 3个半径Fig.3 Radius of three

计算得到同位素链的质子均方根半径、中子均方根半径、电荷均方根半径,以219-224Rn为例,如图3所示。

由图3可以知道,3个半径关系是Rn>Rc>Rp,在重核中,中子数要多于质子数,所以导致了这一现象。随着质量数的改变,半径改变程度不是特别大,有小幅度的变化趋势。从理论上来说,等效DBHF方法能够使每粒子结合能与电荷均方根半径这对共轭量的计算结果同时变得更理想。

根据计算得到的结合能,再利用如下公式[18]:

计算得到各个同位素链的单中子分离能与双中子分离能,以219-224Rn为例进行说明,如图4所示。

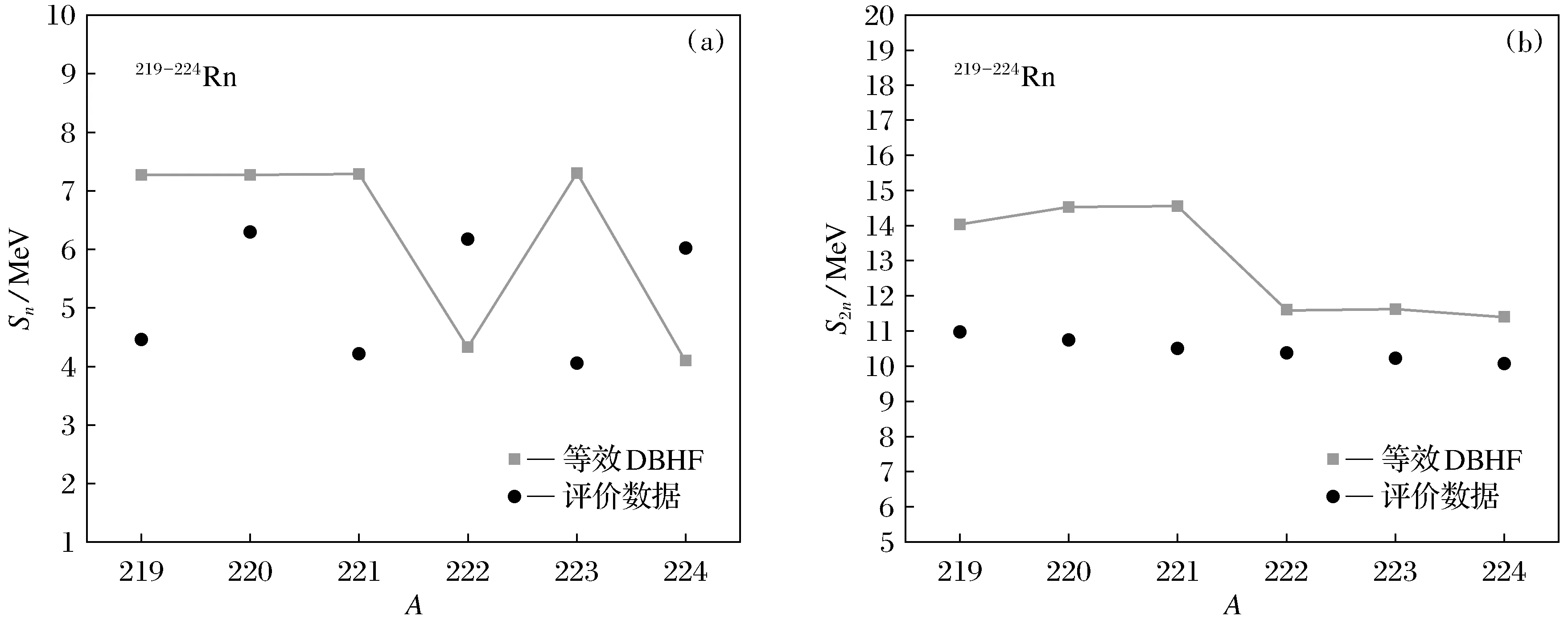
图4 中子分离能Fig.4 Neutron separation energy

由图4(a)可以知道,单中子分离能的评价数据分布很有规律,而计算结果在后半段与其有相反的变化趋势,但整体结果仍在同一个范围区间;由图4(b)可以知道,双中子分离能的实验值近似呈一条平缓向下的直线,计算结果在前半段偏差略大,但在后半段与实验值符合得较好。能够呈现出这种结果与其内部结合能的贡献特点密切相关。

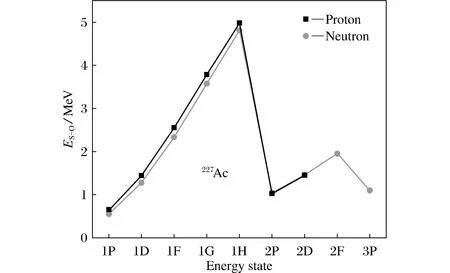
图5 自旋轨道劈裂Fig.5 Spin orbitals split

在计算每粒子结合能的同时,能够输出每个能级对结合能的贡献,根据公式[14]:

Es-o=En,l,j=l-1/2-En,l,j=l+1/2

可以计算得到原子核自旋轨道劈裂的能量差,以227Ac为例,计算结果如图5所示。

根据图5可以知道,227Ac自旋轨道劈裂的能量差在1H-2P有剧烈的变化,在2H-3P有较剧烈的变化,这是壳效应影响的结果。中子轨道劈裂条数多于质子轨道劈裂条数,这是因为重核内部所含的中子数更多。在1P-1H轨道,质子轨道劈裂的能量要多于中子,在1H以后近似相等,而且能够很明显地看到P、D、F、H轨道劈裂的能量在逐渐增大,并且2P要高于1P,2D要高于1D,计算结果符合理论说明,S轨道不能劈裂。

3 总 结

本文首次运用等效DBHF方法计算重核的性质。从计算分析结果来看,在每粒子结合能、电荷均方根半径、质子均方根半径、中子均方根半径、自旋轨道劈裂等方面均有着很好的描述,证明本方法可以推广到重核的相关研究中。

等效DBHF方法是从核子-核子有效相互作用出发,没有自由的可调参数,其中密度依赖的耦合常数在相对论平均场中等效地包含了核子的短程关联效应及DBHF同位旋结构,内部反应机制考虑更为全面。该方法相比于其他方法的计算更加合理、更有说服力,可以将此方法推广到计算分析超重核与丰质子核等远离β稳定线核的性质。