数形结合数学思想方法培养的阶段性简析

金正静

【摘要】数学是人们认识和改造世界的有力工具，数学中最主要的成分始终是思想方法，甚至可以说数学本身就是一种方法.数学中的逻辑推理是受到一系列数学思想方法的控制和引导的，学习数学从根本上讲就是获得数学的思想和方法.实行数学思想方法的教学，既是中国数学教育的特色之一，也是广大数学教师需要达到的一个高端教学目标.

【关键词】数学思想方法;数形结合;中职数学;数学教学

对于数学思想方法，大家耳熟能详，相关出版物数不胜数.然而对于广大数学教师，如何挖掘教材中的数学思想方法，如何有效开展数学思想方法的教学呢？这类文章虽有，但多数只限于操作、领悟、渗透之类，较为空泛，而涉及中职数学的数学思想方法教学的相关研究，更是寥寥无几.

张奠宙先生认为实行数学思想方法的教学，是中国数学教育的特色之一，值得传承和发扬.他对数学思想方法做过深入研究并有许多精彩论述.基于张奠宙先生关于分阶段培养学生数学思想方法的一些思考，本文以上海中职数学教学为例，对中职生数形结合数学思想方法的阶段性培养进行简析.

1 数学思想方法的界定

数学思想和数学方法既相互联系又有区别.数学方法是人们从事数学活动时使用的方法.数学思想还没有成为一个专有名词，其泛指某些有重大意义的、内容比较丰富、体系相当完整的数学思想，比如数理逻辑思想、函数映射思想、方程思想、概率统计思想等.对于上述思想，表述为方法也可以，比如，用“映射”去将复数问题和向量问题对应时，人们就说“映射方法”.而当讨论“映射”的价值，适当的映射的选择，使得问题的内涵在另一领域中变得更容易解决，实现了化难为易时，人们就谓之“映射思想”了.思想重在指导，方法指向操作，数学思想比数学方法在抽象程度上处于更高的层次.为了将两种意思整合在一起，于是就有了“数学思想方法”的提法.

2 数学思想方法在数学教学中的地位

数学教育家傅种孙先生曾言：“几何之务不在知其然，而在知其所以然;不在知其然，而在知何由以知其所以然.”这为数学解题教学标明了三个递进的境界：一是知其然，二是知其所以然，三是知何由以知其所以然.数学解题教学，不能满足于一，应该立足于二而求三.当前，教师应在“何由以知其所以然”上下功夫，这样才有可能在“如何使学生想得到”上有所突破，示以学生思维之道，饯行数学核心素养.

华罗庚先生认为，学习要经过“由薄到厚”“由厚到薄”的过程.以此来审视数学教育，就是要先打好基础，经由知识点链（基本知识的学习）和变式教学（学生解题的强化），把教材读“厚”;再经过数学思想方法的提炼，最终实现把教材“由厚读薄”的过程.

张奠宙先生认为，基于数学教学的自身规律，教师需要把握三个层次：学生基础知识和基本技能的掌握，对学生问题解决能力的培养和学生数学思想方法的掌握.因此，数学思想方法的教学是广大数学教师需要努力达到的一个高端目标.换而言之，学生在学习数学时，若能达到掌握数学思想方法的层次，就达到了数学学习目标的高层次.

人民教育出版社中学数学室主任章建跃教授也指出，完整的数学学习过程应当体现在“明线”和“暗线”的有机融合中，明线是显性的知识体系线，暗线是隐性的思想方法线，注重“明线”与“暗线”的融合，是实现数学内容与数学学科核心素养融合的关键举措.章教授在《数学学习和智慧发展》中特别指出教师专业发展的三大基石是理解数学，理解学生，理解教学，尤其指出教师对“内容所反映的数学思想方法”的理解水平决定了其数学教学所能达到的水平和效果.

3 数形结合数学思想方法培养的阶段性简析

古代数学家刘徽在《九章算术注》中主张“析理以辞，解体用图”，近代数学家华罗庚先生曾说过“数无形，少直观;形无数，难入微;数形结合百般好，隔离分家万事休”.

数和形是研究数学的两个侧面，数是数量关系的体现，形是空间形式的体现.将这两个侧面统一起来，数形结合的实质就是把抽象的数学语言与直观的图形语言有机结合，实现抽象思维和形象思维的和谐统一，更好地把握问题的本质，将所要解决的问题化难为易.

数轴和坐标系的建立，使数和形在宏观上可以有机结合，数形结合是中职数学中最重要、最基本的数学思想方法.在中职数学中，学生能体会到数形结合数学思想方法的章节是集合、不等式、函数、直线和圆、向量、复数等，其中函数既是中职数学的重要内容之一，又是集中体现数形结合数学思想方法的章节.在这几章的教学中，教师应当依据课程内容合理布点，有针对性地进行数形结合数学思想方法的渗透，使学生养成数形结合的意识.然而在实际教学中，数形结合数学思想方法的教学差强人意，主要表现在数形结合数学思想方法的教学没有前后一致、贯穿始终的主线，没有必要的根基.教师在数形结合数学思想方法教学上着墨不够，通常只是走过场，在教学过程中不能螺旋上升，数学思想方法教学的计划性、系统性、层次性、过程性显得不足.

数形结合数学思想方法的教学以数学内容为载体，随着数学内容的变化处于动态变化过程中，教师必须明确数形结合数学思想方法教学所处的阶段及该阶段的教学层次与教学要求.学生只有经历感知、理解、应用、提升的过程，才能形成功能强大的数形结合数学思想方法认知结构，切实发展数学能力，提高数学素养.基于张奠宙先生分阶段培养学生数学思想方法的相关研究，我们以集合、不等式、函数的数形结合数学思想方法教学为例，根据学生的认知规律，把中職生数形结合数学思想方法的形成过程分为以下四个阶段.

3.1 隐性的操作感受阶段

该阶段属于“顺向思维”阶段.这一阶段，学生刚学习了一些数学概念、定理等基础知识，掌握了一些基本技能，尽管这些基础知识和基本技能的后面蕴藏着数学思想方法，但是学生的注意力往往聚焦在基础知识的显性一面.教师在这个阶段的主要教学策略是“让学生探索、构建与掌握知识和技能”，至于背后的数学思想方法应属于“无声语言”，由学生自己在探索、构建与掌握知识中感悟.

在学习第一章“集合”时，我们常常借助韦恩图、数轴图来处理集合的一些运算问题，以形助数，化抽象为具体，简化所要解决的问题.

例1 U={xx<10，x∈N*}，AU，BU，且（瘙綂UA）∩B={6，9}，A∩B={3}，（瘙綂UA）∩（瘙綂UB）={1，7，8}，求集合A，B.

解 利用韦恩图，如图1，把元素放入下图中的相应位置，从而得到A={2，3，4，5}，B={3，6，9}.

图1

例2 已知集合A=（1，2），B=（-∞，3]，求瘙綂RA∩B.

解瘙綂R（A）=（-∞，1]∪[2，+∞），利用数轴图，如图2，很直观地可以得到（瘙綂RA）∩B=（-∞，1]∪[2，3].

图示法是集合的一种重要表示方法，在例1的求解过程中，我们借助韦恩图很好地诠释了集合A，B中的元素，问题变得简单明了.在例2的求解过程中，我们以数轴的“形”来融合“数”，这样有助于启迪思路，理顺解题线索.这样的例子还有很多，在此不一一列举.

图示法直观表示背后蕴藏着的数形结合数学思想方法，属于“隐性的操作感受阶段”，它的主要目的是借用形象的几何直观，帮助学生理解数量关系.教之道在于度，学之道在于悟.在数集的教学中，教师不需要抛出“数形结合”这个词，只需让学生自主建构.在一次次利用图示法解决数集问题后，学生就能初步体会数形结合的基本指导思想，即用“形”的直观来化解“数”的抽象，寻求解题思路，化难为易，从而达到出奇制胜的目的.

3.2 正面的认识和理解阶段

数学教材里不正面阐述数学思想方法.在学生经历了一个“隐性的操作感受阶段”后，限于学生自身的知识储备和能力范围，若教师不对其进行必要的点拨，则他们很可能无法正面认识知识背后的一些数学思想方法.这就需要教师直击要害，反映本质，直接点明背后蕴藏着的一些数学思想方法，并对学生进行有针对性的强化训练，这个阶段称为“正面的认识和理解阶段”.这个阶段的特点是具有明显的导向性，是将内隐的数学思想方法外显传输的阶段，是学生有意识地学习数学思想方法的重要提升阶段.

在这个阶段，教师需要恰时恰点地揭示数学思想方法，使学生形成认知.许多数学内容，书本上是按形式化的方法安排的，而教师在实际教学时要以揭示数学思想方法为主线设计，下面举例来阐述.

例3 已知集合A={（x，y）y=x+1}，集合B={（x，y）y=-x+3}，求A∩B，说明它的几何意义，并在直角坐标系中表示出来.

解 A∩B=（x，y）y=x+1，y=-x+3=（x，y）x=1，y=2={（1，2）}.如图3，集合A表示一次函数y=x+1的图像， 图3即直线l1上的点的集合;集合B表示一次函数y=-x+3的图像，即直线l2上的点的集合.A∩B表示直线l1和直线l2的交点，其坐标（1，2）为二元一次方程组的解.

函数是中职数学课程里的核心概念之一，借助图像分析函数的性质是学习函数的基本思想方法，是数形结合数学思想方法的集中体现.例3表明方程思想和函数思想密切相关：方程y-f（x）=0的全体解就是函数y=f（x）的图像上所有点的坐标（反之亦然）.

例4  解不等式-x2+2x-2>0.

解 原不等式两边同乘-1，得x2-2x+2<0.一元二次不等式x2-2x+2<0所对应的一元二次方程x2-2x+2=0的判别式Δ<0，所对应的一元二次函数y=x2-2x+2的二次项系数为正，抛物线开口向上，函数图像位于x轴上方.如图4，由图像得，不等式x2-2x+2<0的解集为空集，即原不等式-x2+2x-2>0的解集为空集.

例4表明函数与不等式可以相互转化：对函数y=f（x），当y>0时，就转化为不等式f（x）>0，借助函数的图像可解决不等式问题.

在上述两例的讲授过程中，教师有必要正面揭示其背后所隐藏的在直角坐标系下“以数论形”的数形结合数学思想方法：利用坐标系建立了二元有序实数组与平面点集之间的一一对应，把代数问题整体性地映射成几何问题（反之亦然）.这种数学思想方法在后续幂函数、指数函数、对数函数和三角函数等的学习中教师都会陆续地加以正面表述，使学生明确其内涵，不断积累.

总之，在点集的运算和一元二次不等式的教学阶段，教师要抓住思维教学的时机，正面表述并强调数形结合数学思想方法，帮助学生多维度、多视角、多层次地思考问题，体会问题解决的本质和真谛.

3.3 主动运用的训练积累阶段

数学教育形态的灵魂就是数学思想方法，数学思想方法的教学应根据教学内容多层次、递进式展开.在主动运用数学思想方法的训练积累阶段，教师要以强化学生运用这种数学思想方法的意识为依据设计课堂教学，发挥数学思想方法的引领作用，对学生加强训练，并让学生反复经历这个思维过程，使学生有结构、有逻辑地思考，提高解题的层次.

指数函数、对数函数的全部内容都融合了数形结合数学思想方法，这里教师无须在口头上强调，而是让学生在训练中体验和积累.

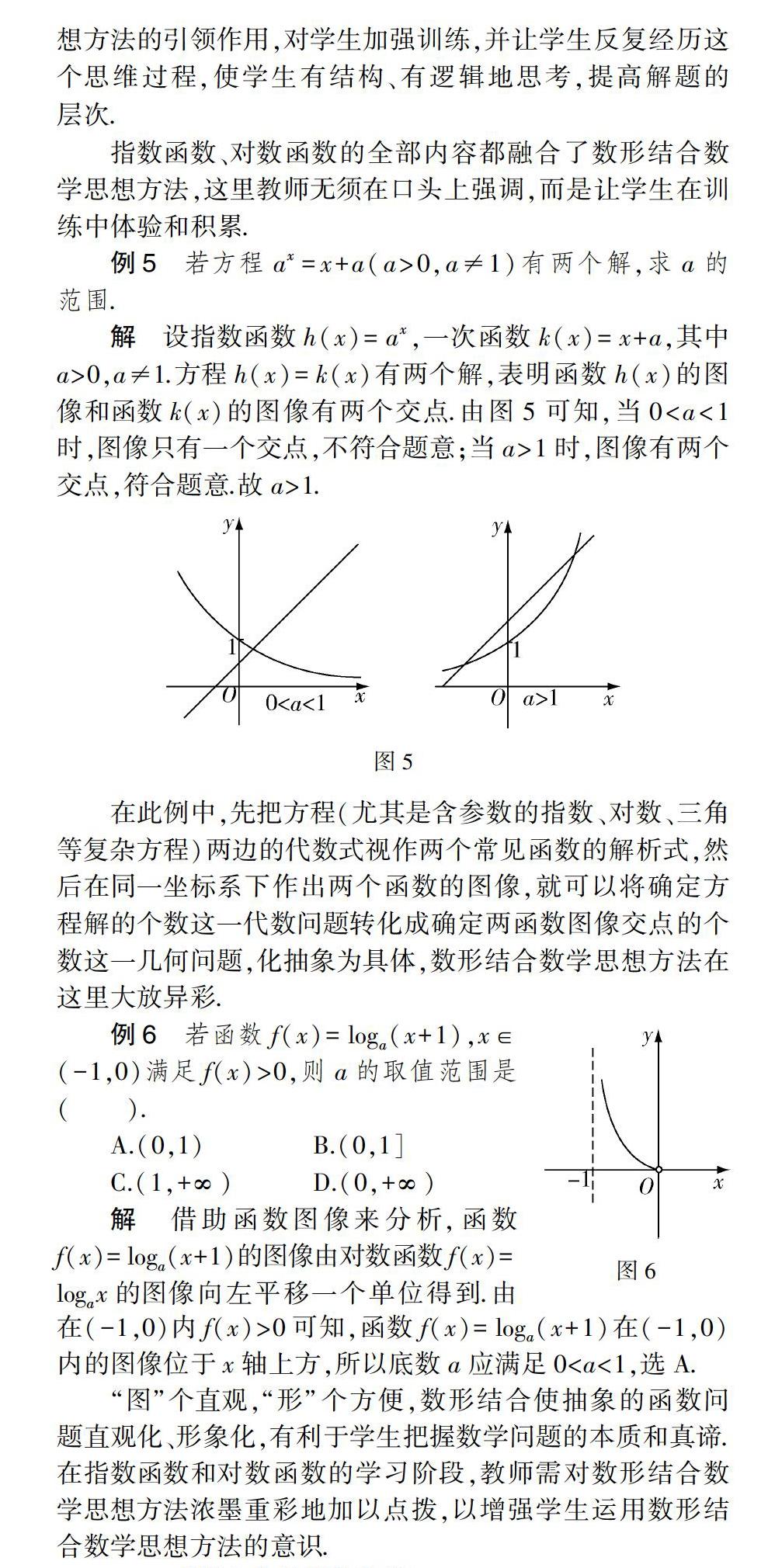
例5 若方程ax=x+a（a>0，a≠1）有两个解，求a的范围.

解 设指数函数h（x）=ax，一次函数k（x）=x+a，其中a>0，a≠1.方程h（x）=k（x）有两个解，表明函數h（x）的图像和函数k（x）的图像有两个交点.由图5可知，当01时，图像有两个交点，符合题意.故a>1.

在此例中，先把方程（尤其是含参数的指数、对数、三角等复杂方程）两边的代数式视作两个常见函数的解析式，然后在同一坐标系下作出两个函数的图像，就可以将确定方程解的个数这一代数问题转化成确定两函数图像交点的个数这一几何问题，化抽象为具体，数形结合数学思想方法在这里大放异彩.

图6例6 若函数f（x）=loga（x+1），x∈（-1，0）满足f（x）>0，则a的取值范围是（  ）.

A.（0，1） B.（0，1]

C.（1，+∞）D.（0，+∞）

解 借助函数图像来分析，函数f（x）=loga（x+1）的图像由对数函数f（x）=logax的图像向左平移一个单位得到.由在（-1，0）内f（x）>0可知，函数f（x）=loga（x+1）在（-1，0）内的图像位于x轴上方，所以底数a应满足0

“图”个直观，“形”个方便，数形结合使抽象的函数问题直观化、形象化，有利于学生把握数学问题的本质和真谛.在指数函数和对数函数的学习阶段，教师需对数形结合数学思想方法浓墨重彩地加以点拨，以增强学生运用数形结合数学思想方法的意识.

3.4 感悟文化修養的阶段

重要的数学思想方法大多以数学文化作为载体，数学思想方法的教学伴随着人们对数学的欣赏.数学是理性思维和想象的结合，是一门美的科学.数和形的结合充分体现了数学的统一美，数学上的对称美、轮换美、简洁美、和谐美、奇异美等形式在图形上的体现更为直观、更为动人.

从深层次来说，数学教育的本质目标是数学育人.因此在感悟文化修养这一阶段，教师需要进行适当的总结，将数形结合数学思想方法提升为学生的文化感悟，乃至文化修养.

在数学家李尚志教授心中，数学如中国诗词一般美丽.李教授认为数学即诗，诗即数学，因此他常常用诗来描述数学.在学完幂函数、指数函数、对数函数后，教师需让学生仔细研读李教授的下面这首诗，学生将别有一番感受.晨雾茫茫碍交通，蘑菇核云蔽长空;化石岁月巧推算，文海索句快如风.指数对数相辉映，立方平方看对称;解释大千无限事，三族函数建奇功.在李教授的心中，数学与大千世界纷呈的自然、社会现象已经交融在一起了.

在学习了幂函数、指数函数、对数函数后，我们会觉得三角函数的图像更是一座美丽的数学山峰.在进行三角函数的教学时，教师可以借助计算机软件，进行三角函数图像的演示，以增加美感.教师可以引导学生从真、善、美三个层面进行欣赏.首先是三角函数之真.正余弦函数是比较神奇的函数，代表着世界的某种本质，那种认为正余弦函数不过只是个数学表达式的观点就过于肤浅了.正余弦函数是最自然、最简单的周期运动的体现，一个点做匀速圆周运动，这个点的位移随时间的变化曲线就是cos x或sin x曲线.其次是三角函数之善.三角函数是波浪的数学模型，蕴含着丰富的人生哲理.昼夜循环潮起伏，冬春更替草枯荣.正余弦曲线和我们的人生何其相似，在巅峰时接踵而来的也许就是低谷，而在低谷时要坚信马上就能看到光明.人在某个时间段总会出现低谷期，不顺心的事情接踵而来.这没有什么，我们要相信终究会再次到达顶峰.再次是三角函数之美.不同函数有不同的美，各种美千姿百态.一次函数之美美在简单明快;二次函数之美美在大起大落;指数函数之美美在一飞冲天;三角函数之美，则涵盖了周期美、对称美、起伏美、统一美，堪称完美.

以数学知识的发生发展过程为载体，遵循学生头脑中数学思想方法的形成规律的数形结合数学思想方法的教学需分阶段进行.数学思想方法的教学不能游离于提出问题和解决问题的过程之外，不能离开具体的教学活动，那种把数学思想方法教学变成空洞说教和华丽术语堆砌的做法实不可取.中职数学教师应当把数学思想方法渗透在日常教学中，要坚持，以收滴水穿石之功，如此对学生数学学科核心素养的培养才能真正落到实处.

【参考文献】

[1]张志勇.数学方法的四个层次[J].数学教学，2019（12）：47-49.

[2]张奠宙，过伯祥，方均斌，等.数学方法论稿（修订版）[M].上海：上海教育出版社，2012.

[3]张奠宙，方均斌.关于数学思想方法的教学[J].中学数学月刊，2012（06）：1-3.

[4]章建跃.核心素养导向的高中数学教材变革（续3）——《普通高中教科书·数学（人教A版）》的研究与编写[J].中学数学教学参考，2019（25）：5-11.

[5]章建跃.数学学习与智慧发展[J].中学数学教学参考，2015（07）：4-10.

[6]顾亚萍.数形结合思想方法之教学研究[D].南京：南京师范大学，2004.

[7]孙婷婷.浅析关系映射反演方法的教学[J].中学教学参考，2019（05）：5-6.

[8]任伟芳，华婧.欣赏三角函数波浪起伏的和谐美：以正弦函数、余弦函数性质2的教学设计为例[J].中学数学教学参考（上旬），2016（01）：5-9.

[9]孙朝仁，臧雷.“数学思想方法研究”综述[J].中学数学教学参考，2002（10）：28-30.