基于ICEEMD-EFICA联合降噪的滚动轴承故障诊断研究*

宋宇宙，刘兆亮

(河南工业大学 机电工程学院，河南 郑州 450001)

0 引 言

滚动轴承作为旋转机械中应用最广泛、最易发生故障的零部件之一，其健康状态将直接影响到机械设备能否正常运转。因此，对滚动轴承进行早期故障特征提取与诊断分析具有十分重要的意义[1-2]。但滚动轴承早期故障信号常被淹没于强背景噪声中，使得故障特征信息提取困难，严重影响了滚动轴承早期故障诊断的效果。

改进后的完备总体经验模态分解(ICEEMD)是由COLOMINAS M A等人[3]于2014年提出的一种新的信号处理方法，该方法在CEEMD基础上进行了改进，利用各模态当前的局部均值重新定义了真实模态；从而克服了传统EMD算法模态混叠现象，解决了EEMD算法中存在的计算量大、分解完备性差等问题。与CEEMD相比，含噪数据分解后，有效信息主要集中在较少的模态分量中,使随机噪声得到有效抑制[4，5];吴凯等人[6]利用ICEEMD算法有效抑制了脑血氧信号中的基线漂移和高频噪声，提高了数据的精确度;杨凯等人[7]利用ICEEMD算法，较好地降低了随机噪声，提高了地震资料信噪比;张欢等人[8]将ICEEMD与近似熵相结合，得到了更清晰、稳定的脑电去噪结果，解决了IMF盲目选取导致的去噪失准及虚假模态等问题。

EFICA算法是一种盲源分离技术，被广泛应用于振动信号处理领域。该算法对FastICA进行了改进，实现了非线性函数的自适应选择，从而可以达到分离精度最佳的效果。徐元博等人[9]将EEMD与EFICA相结合，实现了复合故障信号频率特征的提取。

为了实现良好的降噪效果，准确提取轴承故障信息，本文提出ICEEMD与EFICA联合降噪方法；首先对振动信号进行ICEEMD分解；然后将得到的IMFs利用峭度准则重组，并作为盲源分离的输入矩阵；最后通过EFICA降噪分离，提取出故障特征成分，辨别轴承故障。

1 算法原理

1.1 ICEEMD算法原理

为减少冗余模态影响，ICCEMD在CEEMD的基础上，从原始信号中去除估算局部均值，从而降低了信号分解后模态中的残留噪声。其具体分解步骤如下：

(1)设立一个滚动轴承信号。在其中加入高斯白噪声，生成新信号，如下式所示：

xi=x+βkwi

(1)

式中：x—原始滚动轴承信号；xi—新生成的滚动轴承信号；wi—第i组添加的高斯白噪声；βk—xi的计算系数，βk=ε0std(rk)；ε0—βk的计算系数；rk—第k个余项；std—标准差运算；

(2)定义两种算子M(·)和Ek(·)。

M(·)与Ek(·)的关系如下式所示：

M(x)=x-Ek(x)

(2)

式中：Ek(·)—EMD分解得到的第k个模态；

(3)通过对EMD的计算，获得第一个IMF分量，如下式所示：

(3)

则其一级残差为：

r1=x-IMF1

(4)

(4)计算第2个残差和第2个模态，如下式所示：

(5)

IMF2=r1-r2

(6)

(5)依此类推，计算第k个残差和第k个模态，如下式所示：

(7)

IMFk=rk-1-rk

(8)

(6)重复步骤(5)，直至残差不能被分解，从而获得全部的IMF。

1.2 峭度准则

峭度是无量纲参数，对冲击信号特别敏感，适用于表面损伤类故障的诊断，尤其是轴承早期故障的诊断。

当轴承健康运行时，振动信号的幅值分布接近正态分布，峭度值约为3；当轴承发生早期故障时，由早期局部故障引发的冲击成分使正态分布发生偏移或分散，峭度值增大；峭度值越大，轴承故障冲击信号的特征信息越易提取。

峭度K是反映随机变量分布特性的数值统计量，如下式所示：

(9)

式中:E(x)—x变量的期望值；x—振动信号；μ—振动信号的均值；σ—振动信号的标准差。

1.3 EFICA算法原理

EFICA是基于FastICA的改进算法，依据单位方差约束找到具有最小熵的不相关信号；该算法能够自适应地选择非线性函数，具有较高的分离精度，可用于非高斯信号。

算法步骤分为以下3步：

(1)对观测数据均值和白化等进行预处理后，运行对称FastICA算法，直至收敛；

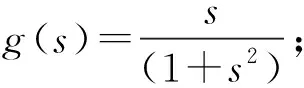
(3)微调和细化，以提高最终分离的准确度。每次微调都要利用单一对称FastICA自适应选择非线性函数迭代来处理。

2 ICEEMD-EFICA降噪方法研究

ICEEMD-EFICA方法通过ICEEMD分解构造虚拟信号，解决了单通道盲源分离的欠定问题，利于实现ICA的降噪作用。

将通过ICEEMD分解获得的IMF，根据峭度准则重组成虚拟信号和振动冲击信号，作为盲源分离的输入矩阵；然后采用EFICA算法进行降噪解混，可以解决单一ICEEMD方法受无关噪声源信号影响的不足，从而准确、快速地辨别出其故障特征。

其方法的流程图如图1所示。

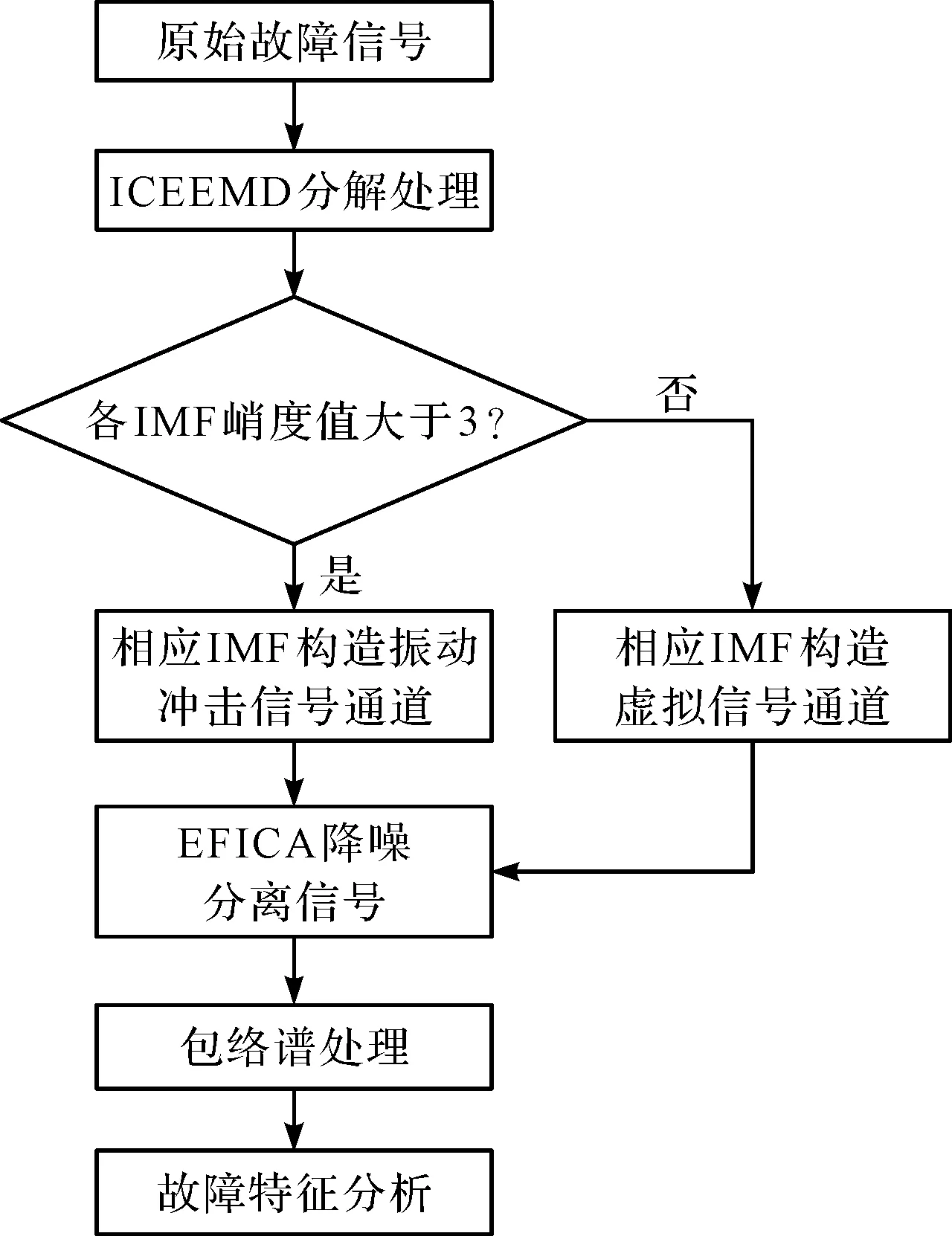
图1 方法流程图

3 实验验证

3.1 轴承故障诊断实验

在SpectraQuest公司推出的轴承故障模拟试验台(MFS)上，笔者进行滚动轴承早期故障诊断实验。

实验选用内圈发生早期故障的轴承进行实验，轴承型号为MB ER-10K，轴承参数如表1所示。

表1 轴承参数

实验中，采样频率为10 240 Hz，采样时长10 s；电机实际转速为1 793 r/min。

轴承转频fr与内圈故障特征频率fi计算方法如下式所示：

(10)

(11)

式中：n—转速；Z—滚珠个数；D—节圆直径；d—滚珠直径；θ—接触角。

由式(10，11)可计算得出其转频为：29.88 Hz,其内圈故障特征频率为147.85 Hz。

3.2 实验与结果分析

滚动轴承内圈故障是局部点蚀故障，其转轴运转过程中，故障点周围的载荷密度会发生周期性变化，该变化将使振动信号发生以转轴频率为调制频率的幅值调制现象[10，11]。所以，在内圈早期故障信号中应包含转频、故障特征频率、倍频，以及以故障频率为中心、转频为边带的调制频率。

滚动轴承内圈故障信号频谱如图2所示。

图2 内圈故障信号频谱

由图2可知：频谱中，转频、内圈故障频率及其倍频完全淹没于低频噪声中，不能实现提取。因此，只通过频谱来判别滚动轴承内圈的故障特征十分困难。

此处笔者利用本文方法对故障信号进行处理，故障信号经ICEEMD自适应分解得到9个IMF。

内圈故障信号IMFs分量时域波形如图3所示。

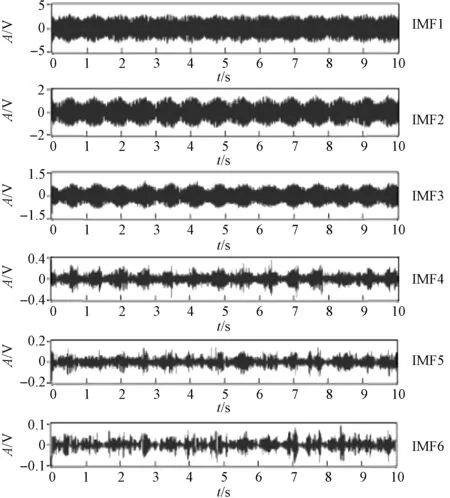
图3 内圈故障信号IMFs分量时域波形

由图3可知，从IMF1到IMF9模态分量频率逐渐降低，表明分解效果较为准确。

分别计算9个IMF的峭度值，IMFs分量峭度指标如表2所示。

表2 IMFs分量峭度指标

由表2可知：分量1、2、4、5的模态分量峭度值大于3，表明以上分量包含较多的冲击成分，可重构为振动冲击信号；其余模态分量重构为虚拟通道信号。重构信号经EFICA降噪解混，完成信噪分离；最后，对最佳估计信号进行包络谱分析。

ICEEMD-EFICA内圈包络谱如图4所示。

图4 ICEEMD-EFICA内圈包络谱

由图4可知：该方法可以准确地识别出能量幅值最大的滚动轴承内圈早期故障频率(fi)147.7 Hz，且可以精确地定位到其5倍频；转频(fr)29.8 Hz、二倍转频2fr幅值明显；以故障频率为中心，转频为边带的调制频率(如：fi+fr)能够准确找出，所得故障频率与理论计算故障频率基本一致。

3.3 对比分析

与CEEMD-EFICA方法进行对比分析。CEEMD-EFICA内圈包络谱如图5所示。

图5 CEEMD-EFICA内圈包络谱

由图5可知：虽然可以找出故障特征频率及其2倍频和调制频率，但故障特征频率(fi)147.7 Hz的能量幅值并非最大，最大值位于调制频率(fi-3fr)58.2 Hz，易将58.2 Hz判别为其他故障频率，不利于内圈故障的提取及诊断分析，甚至易产生误判。

对比图4和图5可知，ICEEMD-EFICA降噪法可以有效地抑制无关噪声，突出故障特征频率，便于故障信息的高效、准确提取及诊断分析。

笔者利用峭度值(K)和信噪比(SNR)对两个算法的降噪效果进行评定，其评定结果如表3所示。

表3 降噪评定结果

由表3可知：基于ICEEMD-EFICA方法得到的信号峭度值更大，是经CEEMD-EFICA处理后得到信号峭度值的1.2倍；根据峭度准则可知，其包含更多的轴承故障冲击成分，进而其故障特征频率也更容易被提取；同时，用本文方法得到的SNR大，比经CEEMD-EFICA方法处理得到的信号的SNR增加了24.76%。

由此可见，本文所提方法降噪效果更加显著。

4 结束语

(1)针对滚动轴承早期故障信号十分微弱，故障特征提取困难的问题，笔者提出了ICEEMD与EFICA联合降噪方法，该方法解决了单一ICEEMD方法受无关噪声源信号影响的不足和单通道盲源分离的欠定问题；能够提取出淹没于强噪声中的振动冲击信号；

(2)笔者利用ICEEMD与EFICA联合降噪方法对滚动轴承早期故障进行实验分析。结果表明：利用该法可以准确、清晰地辨别出轴承内圈早期故障频率、倍频及其转频特征，且最大能量幅值位于故障特征频率上。与CEEMD-EFICA方法对比，采用联合降噪方法其SNR增加24.76%。

由此可以证明：该方法去噪效果良好，突出了故障特征频率；该结论为滚动轴承早期故障判别提供了新的方法。