基于交叉耦合与迭代学习的伺服系统运动控制研究*

王慧霞，郭润兰，赵 强，黄 华

(兰州理工大学 机电工程学院，甘肃 兰州 730000)

0 引 言

随着航空、航天等技术的飞速发展，对涡轮叶片、船用整体叶轮、火箭发动机喷管等高性能复杂曲面零件的需求越来越大，而这类零件的多轴数控精密加工技术成为工业领域的研究热点和难点[1]。

为了保证复杂曲面零件的高性能，对其轮廓精度的要求越来越高。以航空发动机叶片为例，如果轮廓精度得不到保证，将严重影响航空发动机的安全性和可靠性，从而可能引发灾难性的航空事故[2]。然而，数控机床动态特性的限制，导致的轮廓误差，成为影响高性能复杂曲面零件加工精度的重要因素。轮廓误差是指机床在多轴轮廓跟踪任务中，从机床实际运动位置到所需曲面轮廓的正交异性距离，是由伺服滞后、动力学失配、外部干扰等因素引起的。减小轮廓误差对于提高数控系统的性能，实现高速、高精度加工具有重要意义。

因此，对降低多轴数控加工中轮廓误差的研究有重要的理论意义和应用价值。

自20世纪80年代以来，为了减少多轴数控加工中的轮廓误差，研究人员对此进行了大量的研究。在三轴数控加工中，特别是在二维轮廓跟踪任务中，已经出现了许多减小轮廓误差的方法，主要有离线方法、插值器设计、跟踪控制器、交叉耦合方法、集成方法等。这些方法可归为两大类：(1)间接减小法；(2)直接减小法。

间接减小法主要是通过减小所有进给轴的跟踪误差，间接地减小轮廓误差；如零相误差跟踪控制[3]、自适应控制[4]、滑模控制[5]、迭代学习控制[6]等。这些控制方法对于单轴的跟踪误差有很好的抑制效果，其中迭代学习控制(iterative learning control, ILC)由于不要求有确切的受控对象模型，并且在模型参数变化时，仍然可以通过迭代学习使位置输出轨迹实现高精度的跟踪，在众多方法中脱颖而出。然而，虽然轮廓误差是由单轴跟踪误差引起的，但单轴跟踪误差的减小并不一定能确保轮廓误差得到减小，经常出现曲线上一个点的跟踪误差大于另一个点的跟踪误差，但轮廓误差却比其小的现象。因此，仅采取间接减小法并不能确保轮廓精度得到提升。

为解决该问题，直接减小法应运而生。KOREN Y[7]在1980年首次提出了一种交叉耦合控制(cross-coupling control, CCC)方法，成为了目前直接抑制轮廓误差的主流方法。由于单轴控制命令不仅由其自身的输出决定，而且还取决于其他轴的输出，被称为交叉耦合控制。自CCC问世后，许多研究者将CCC设计成多种形式进行轮廓误差的抑制。如CHEN S Y[8]将CCC与PID控制进行结合，李小力等[9]将CCC与自适应控制进行结合，等等；证明了CCC对于多轴运动控制时直接减小轮廓误差有很好的抑制效果。

综上所述，ILC跟踪控制对于减小单轴跟踪误差的效果优越，但对于多轴运动控制时轮廓误差的减小效果一般；而CCC则对于多轴运动控制时，直接减小轮廓误差有很好的效果，却不能减小单轴的跟踪误差。

因此，为了使轮廓加工精度达到最佳，本文结合ILC和CCC的优点，引入交叉耦合和迭代学习来建立两轴间的协调关系，以及减小单轴跟踪误差，通过设计的变增益交叉耦合迭代学习控制器，使数控机床进给伺服系统可以根据轮廓误差模型计算出轮廓误差在各轴的分量，并通过一定的增益比例补偿到各个轴；同时，迭代学习控制器不断修正各轴的控制信号，使轮廓误差不断降低，最终达到使加工产品轮廓加工精度提高的目的。

1 进给伺服系统模型

对系统进行仿真研究时，必须先得到系统的数学模型。本文参考文献[10，11]整理的数控机床进给伺服系统建模方法，对数控机床进给伺服系统的数学模型进行简化整理，得到其中x轴的数学模型为：

(1)

式中：KP—比例系数；KV—积分系数；J—转动惯量；B—粘性摩擦。

在数控机床进给伺服系统中，其他轴通常具有与上述x轴相同的数学模型，因此此处不再讨论。

1.1 学习控制器的设计

由于迭代学习控制适用于具有重复运动属性的受控对象，ILC可以在一定的时间间隔内，完成对跟踪轨迹完全追踪的任务[12]。

迭代学习控制原理如图1所示。

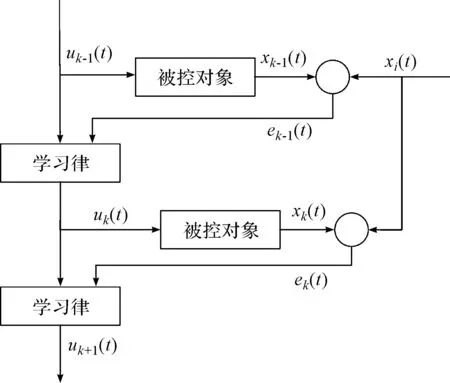
图1 迭代学习控制原理图xi(t)—x轴的位置输入；xk-1(t)—控制系统进行第k-1次迭代时的位置输出；xk(t)—控制系统进行第k次迭代时的位置输出；uk-1(t)—第k-1次迭代时输入的控制信号；uk(t)—第k次迭代时输入的控制信号；uk+1(t)—第k+1次迭代时输入的控制信号；ek-1(t)—第k-1次系统的跟随误差；ek(t)—第k次系统的跟随误差

在图1中，其学习过程为：第k次的控制信号uk(t)存到存储器里，并在第k+1次迭代时，与第k+1次产生的跟随误差一起构造出新的控制信号uk+1(t)，也就是系统产生的跟随误差被ILC控制器处理后，得到新的控制信号，在下一次迭代时再反馈给系统；通过不断地学习，跟随误差不断地减小，当误差减小到设定的值时，则停止迭代计算。

采用P型迭代学习控制律，学习律表示如下：

uk+1(t)=uk(t)+Γek+1(t)

(2)

ek+1(t)=xd(t)-xk+1(t)

(3)

式中：xd(t)—理想输入轨迹；ek+1(t)—跟随误差；Γ—学习增益；xk+1(t)—第k+1次迭代时的位置输出。

对公式(2)(3)进行拉普拉斯变换，得到：

uk+1(s)=uk(s)+Γek+1(s)

(4)

ek+1(s)=xd(s)-xk+1(s)

(5)

依据图1及公式(4)(5)可以得到：

xk+1(s)=Gv(s)uk+1(s)

(6)

由公式(4)(5)(6)可以推出相邻两次误差之间的关系：

ek(s)=(1+Gv(s)Γ)ek+1(s)

(7)

公式(7)变形后可以得到：

(8)

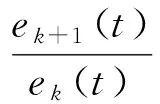
(9)

收敛性得到证明。

1.2 单轴迭代学习控制器误差仿真实验

为了验证所设计的单轴迭代学习控制器对于减小跟踪误差的效果，此处利用MATLAB/Simulink环境搭建了系统控制模型，以进行仿真验证。给定位置跟踪信号为一复杂轨迹：xd(t)=0.1t+0.5sin(t)，设置系统总的仿真时长为2 s，仿真步长为0.1。

仿真实验采用的电机仿真参数和学习增益如表1所示。

表1 仿真参数和学习增益

经过仿真，获得进给伺服系统在P型闭环迭代学习控制律下跟踪期望轨迹的迭代过程，如图2所示。

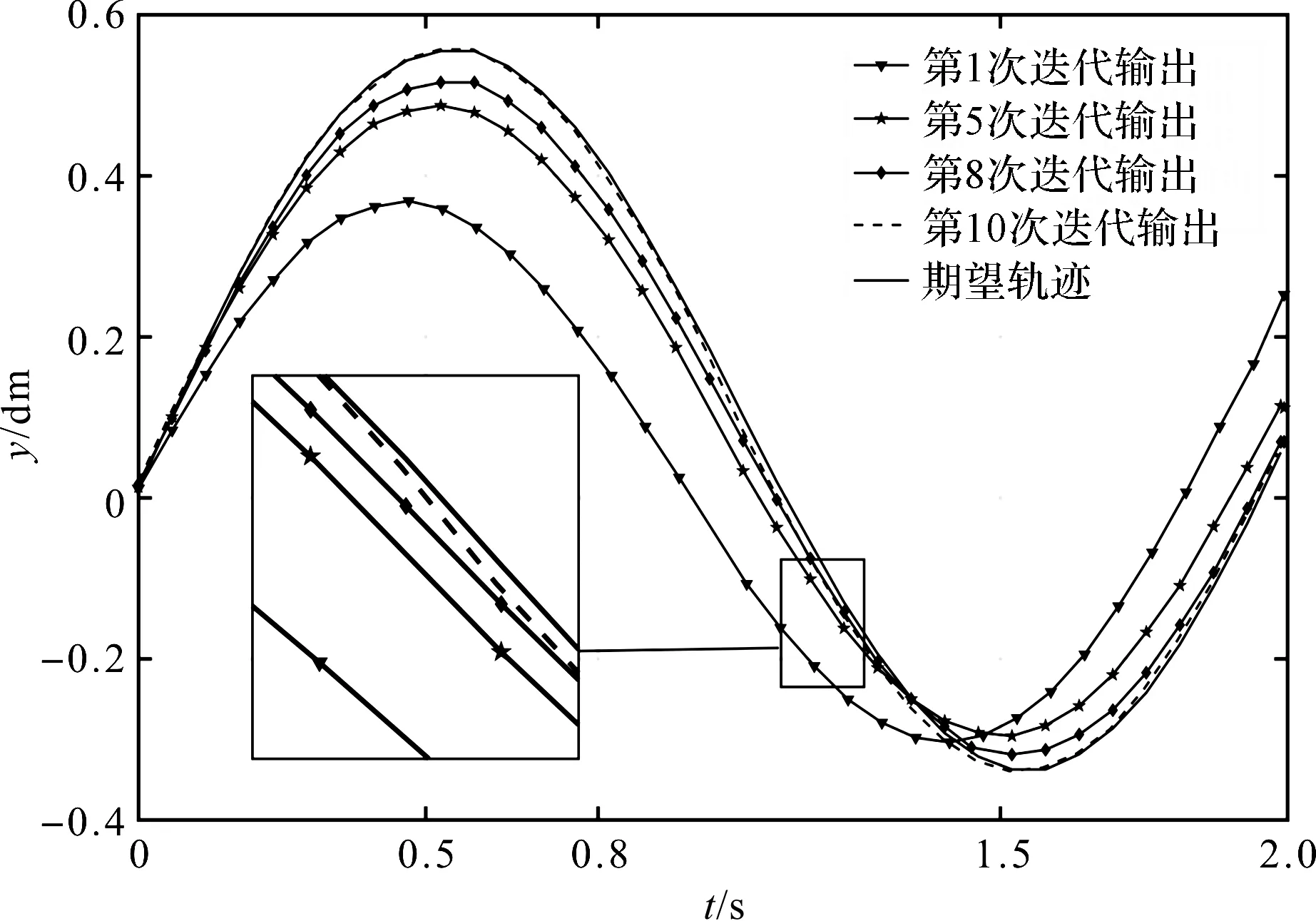
图2 伺服系统在P型闭环迭代学习控制律下跟踪期望轨迹的迭代过程

图2是单轴迭代学习控制器的仿真结果，图2中除了期望轨迹，还保留了第1、5、8、10次的迭代结果。从伺服系统在P型闭环迭代学习控制律下跟踪期望轨迹的迭代过程图，以及图2中的标记部位放大图，可以明显看出：随着系统迭代次数的增加，系统的实际输出轨迹逐渐接近期望输出轨迹，达到了对期望轨迹的良好跟踪效果。

为了能更清楚地显示系统的迭代输出误差是否随着迭代次数的增多而最终收敛到零，此处给出了10次迭代过程中，最大绝对误差与迭代次数关系曲线图如图3所示。

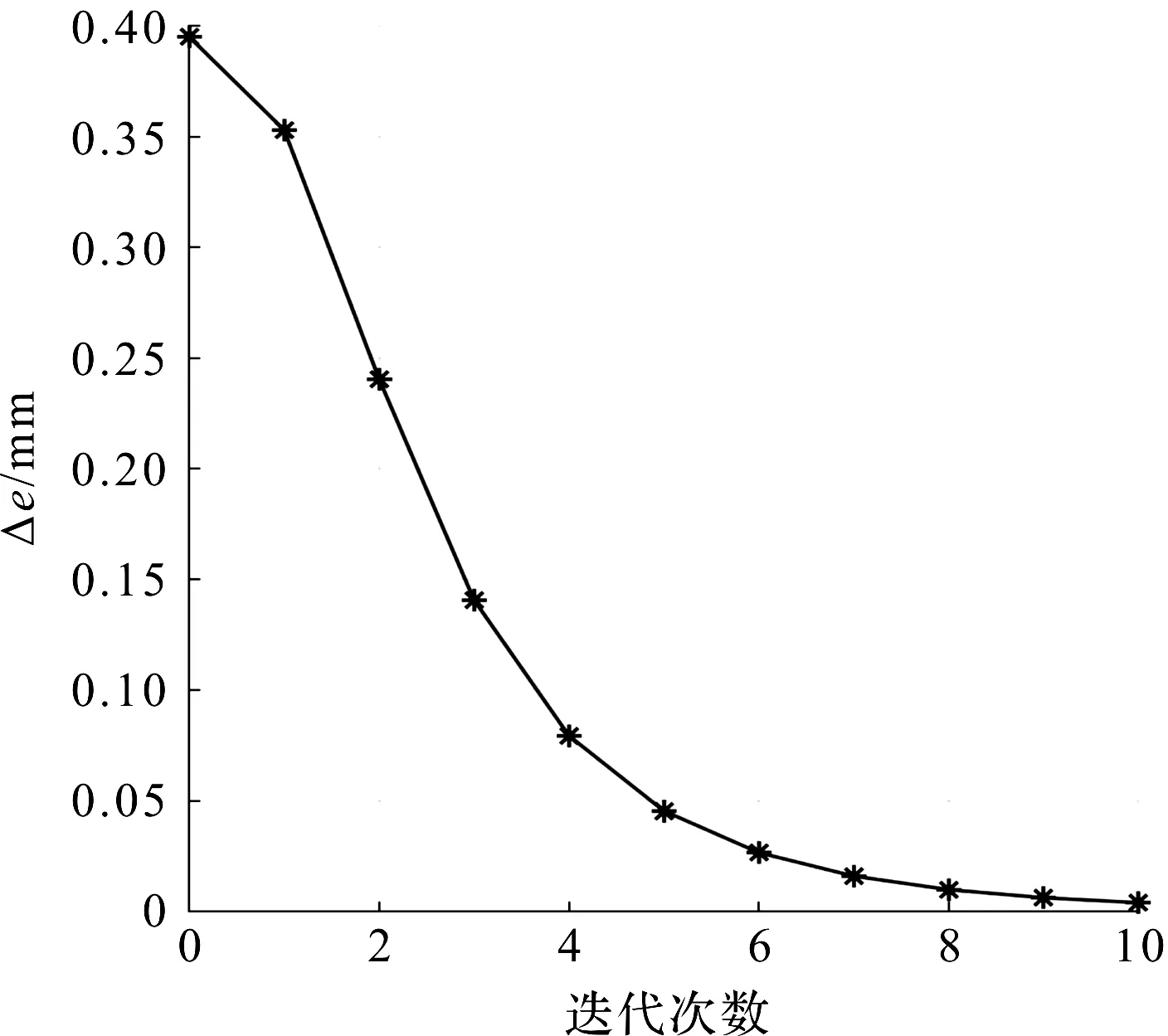
图3 10次迭代过程中最大绝对误差与迭代次数

从图3中可以发现：系统在10次迭代过程中，初次迭代时，由于系统输出还不收敛，出现了较大的误差；然而随着系统迭代次数的不断增多，系统输出轨迹的最大绝对误差在逐步减小；在迭代到第10次时，系统在t∈[0,2]时间段内输出的最大绝对误差基本收敛到零。

因此，据关系曲线图可以证明，所设计的单轴迭代学习控制器能有效降低系统的跟随误差。

2 交叉耦合控制器设计

2.1 变增益交叉耦合控制器

上述设计的迭代学习控制器可以很好地降低单轴的跟踪误差。但是，仅仅通过减小单轴的跟踪误差，并不能确保多轴系统的轮廓误差得到了良好的抑制。因为，当系统进行多轴运动控制时，运动轴之间的匹配性较差，轮廓加工精度也会降低。因此，使用轮廓误差指标评价多轴系统的轮廓加工精度性能，比使用跟踪误差作为评价指标更为准确。

Koren提出的交叉耦合控制可以直接消除多轴运动系统的轮廓误差。其基本控制原理是：多轴运动系统的轮廓误差，由各单轴的跟踪误差经过实时轮廓误差估计模型计算得到，经过交叉耦合控制器的作用产生一个新的控制信号，再经过轮廓误差分配模型补偿到各轴，以消除每个轴对其他轴的影响，进而达到提高多轴运动系统轮廓加工精度的目的。目前，将交叉耦合控制器输出的轮廓误差补偿控制量分配给各运动轴的方式中，最常用的有3种：(1)等增益误差分配方法；(2)比例误差分配方法；(3)变增益误差分配方法。

在上述3种方法中，可变增益误差分配方法能够依据各单轴反馈回来的信息，对轮廓误差估计模型估计的误差信息进行处理，并使用最优的增益比对各单轴进行补偿，从而达到提高轮廓加工精度的目的。

因此，本文选用变增益误差的分配方法，设计基于变增益交叉耦合的多轴运动控制器，来减小轮廓的误差。

变增益交叉耦合控制原理如图4所示。

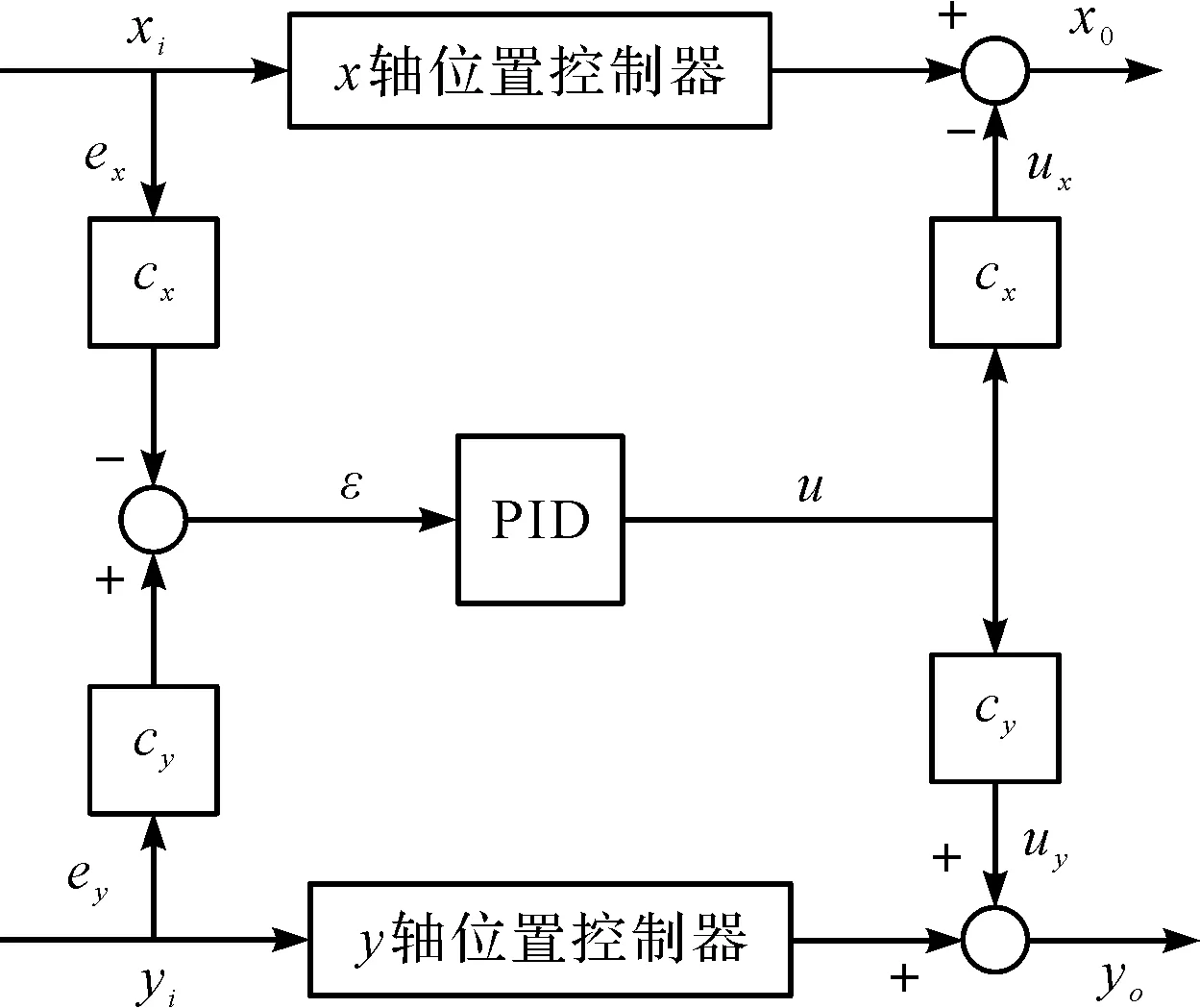
图4 变增益交叉耦合控制器原理

在图4的变增益交叉耦合控制原理中，系统轮廓误差ε与各轴的误差存在着以下的关系：

ε=cyey-cxex

(10)

式中：cx,cy—交叉耦合增益。

ex=xi-xo,ey=yi-yo

(11)

式中：xi—x轴的期望轨迹；yi—y轴的期望轨迹；xo—x轴的实际轨迹；yo—y轴的实际轨迹。

ux=ucx,uy=ucy

(12)

式中：u—经过PID控制器处理之后的轮廓误差；ux—补偿到x轴的误差；uy—补偿到y轴的误差。

其中，轮廓误差与跟踪误差存在以下的关系：

ε=eycosθ-exsinθ

(13)

比较式(10，13)可知：cx=sinθ，cy=cosθ。当期望轨迹为一个线性直线时，斜率是固定的，此时得到的x轴和y轴的增益系数也是不变的。

由此可见，当轨迹路径为线性轨迹时，直接将该线段与x轴的夹角θ代入cx与cy即可；当轨迹路径为非线性时，cx与cy会跟随x轴和轨迹曲线的切线之间的夹角θ的变化而不断改变，即时补偿x、y轴的耦合误差，达到了变增益交叉耦合控制的目的。

2.2 迭代学习交叉耦合控制

变增益交叉耦合控制方法能够有效提高多轴运动系统的轮廓跟踪能力，减小系统的轮廓误差。然而该方法只是减小了轮廓误差，并没有改进单轴的跟随误差。

为了提高单轴跟踪精度，在单轴位置环采用迭代学习控制的策略，这是一种对受控对象无精确模型要求的综合控制方法，对运动系统的数学模型要求不严格，对先于经验的知识要求不多并且计算量少，而且能够有效提高跟踪性能。

基于上述控制方法的特点，以及前文对ILC控制的介绍，笔者将单轴的迭代学习控制和双轴的变增益交叉耦合控制进行融合，设计了一种基于变增益交叉耦合的迭代学习控制器。

变增益交叉耦合迭代学习控制器原理框图如图5所示。

由图5可以得到：

(14)

将式(10，11，14)进行整理，可得到ε的数学表达式为：

(15)

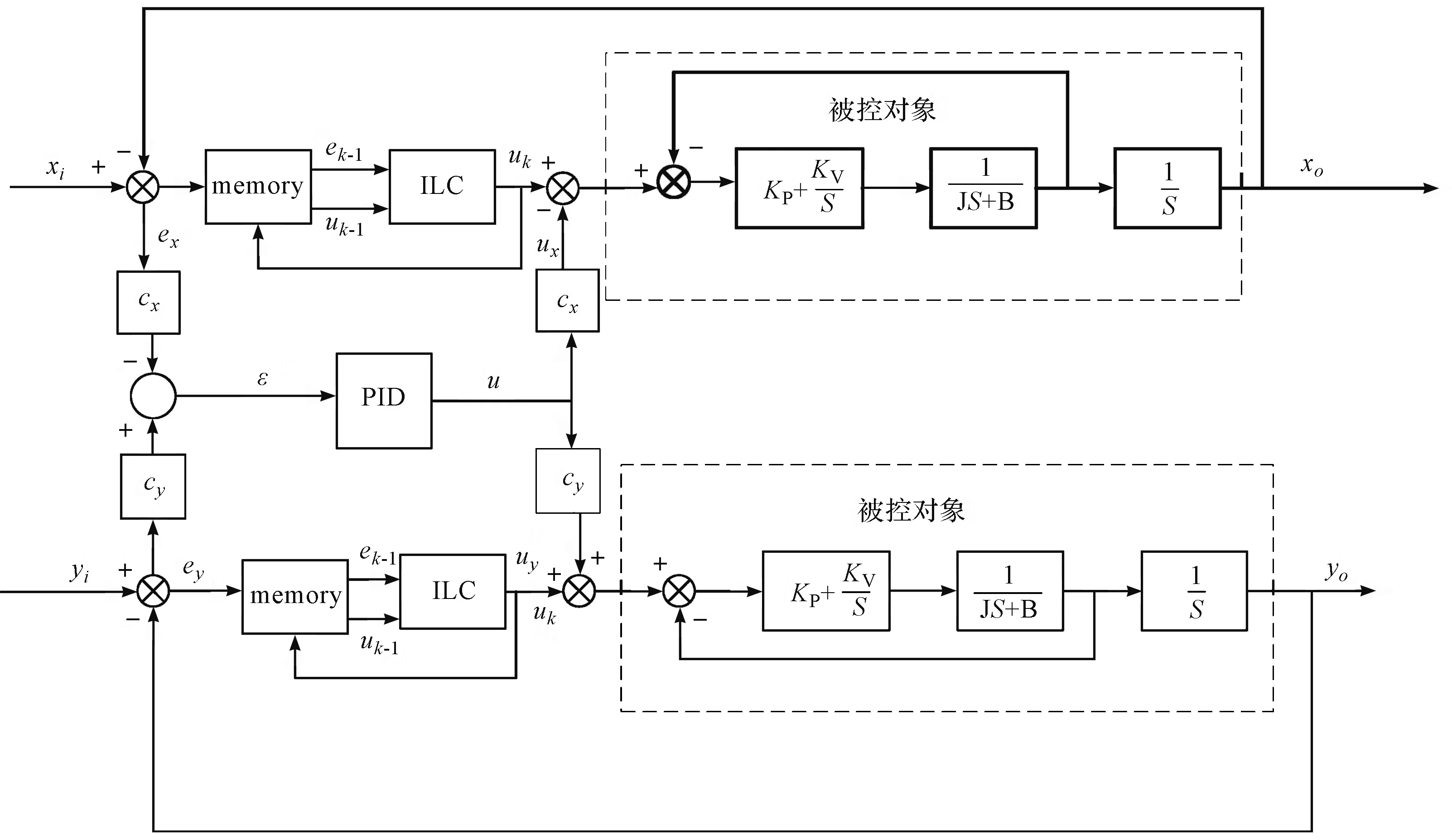
图5 变增益交叉耦合迭代学习控制器原理框图

3 仿真验证及结果分析

为了验证所设计的变增益交叉耦合迭代学习控制器，对改善数控机床进给伺服系统双轴运动的轮廓跟踪能力和降低单轴跟踪误差的有效性，此处使用MATLAB/Simulink建立模型，并进行相应的仿真分析。

其中，ILC+CCC的Simulink模型图如图6所示。

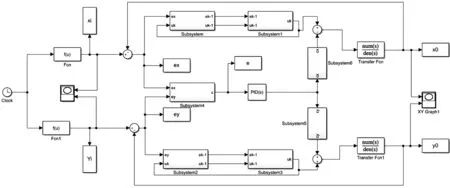
图6 ILC+CCC Simulink模型图

在图6的仿真模型中，被控对象所采用的参数与表1的参数一致，变增益交叉耦合控制器PID的参数分别为：P=0.2，I=20，D=0.5。

该试验用于如下对比：

(1)传统的PID单轴控制方法和无交叉耦合控制对追踪理想轨迹过程中产生的轮廓误差；

(2)传统的PID单轴控制方法加交叉耦合控制对追踪理想轨迹过程中产生的轮廓误差；

(3)本文所设计的迭代学习单轴控制方法加变增益交叉耦合控制方法对追踪理想轨迹过程中产生的轮廓误差。

本文选取三叶玫瑰轨迹作为理想输入轨迹，其数学表达式为：

x=sin(3t)cost,y=sin(3t)sint

(16)

式中：t∈[0,2π]。

3种控制方法跟踪的实际轨迹与理想轨迹对比如图7所示。

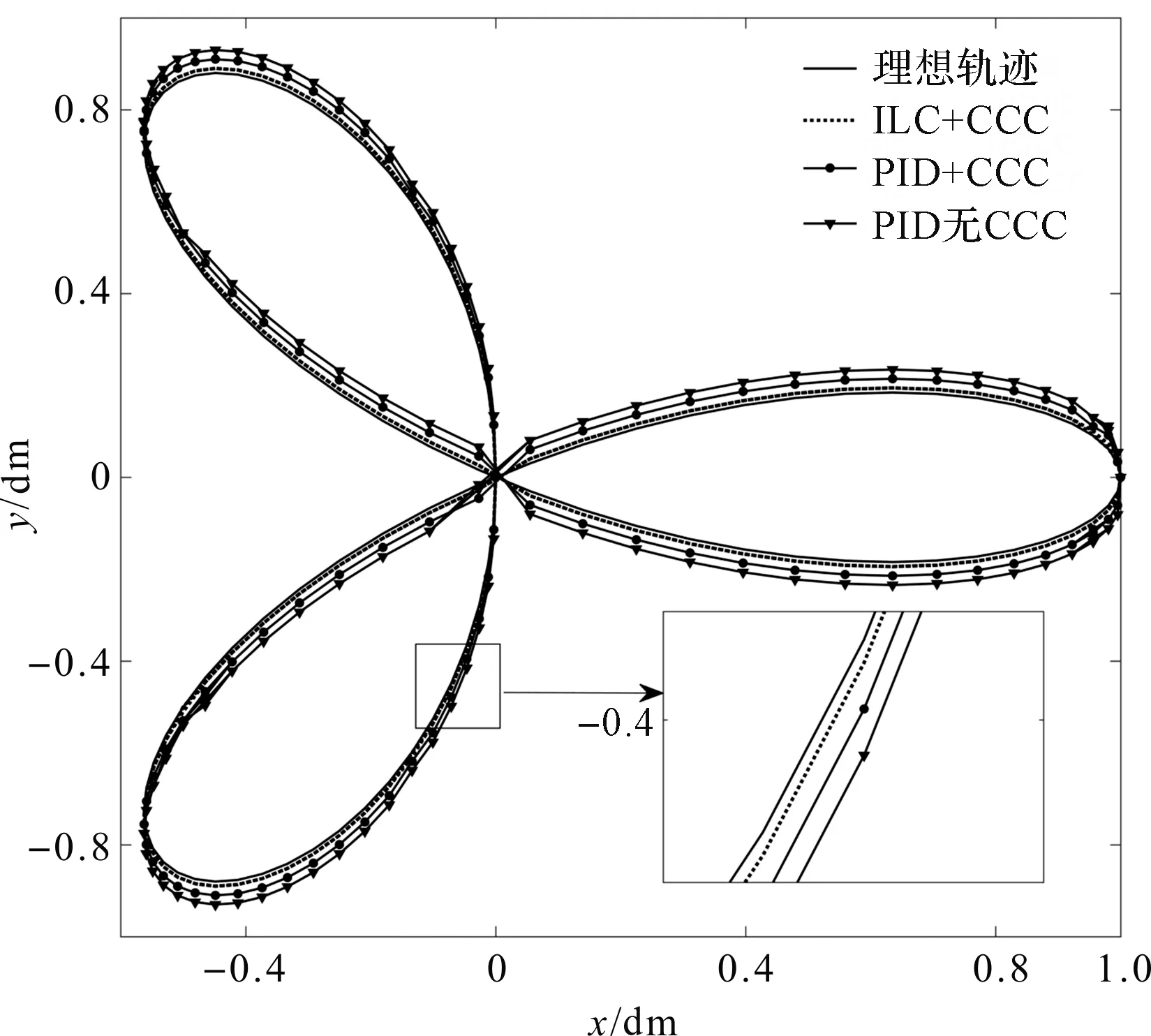
图7 3种控制方法跟踪的实际轨迹与理想轨迹对比图

通过图7的3种控制方法追踪的实际轨迹曲线与理想轨迹曲线以及其局部放大图对比可知：ILC+CCC控制方法得到的实际轮廓与期望轮廓最为接近，PID无CCC控制方法的追踪效果最差。

为了更进一步展示3种控制方法对于减小轮廓误差的效果，笔者分别给出了3种控制方法对于跟踪理想轨迹时产生的轮廓误差，如图8所示。

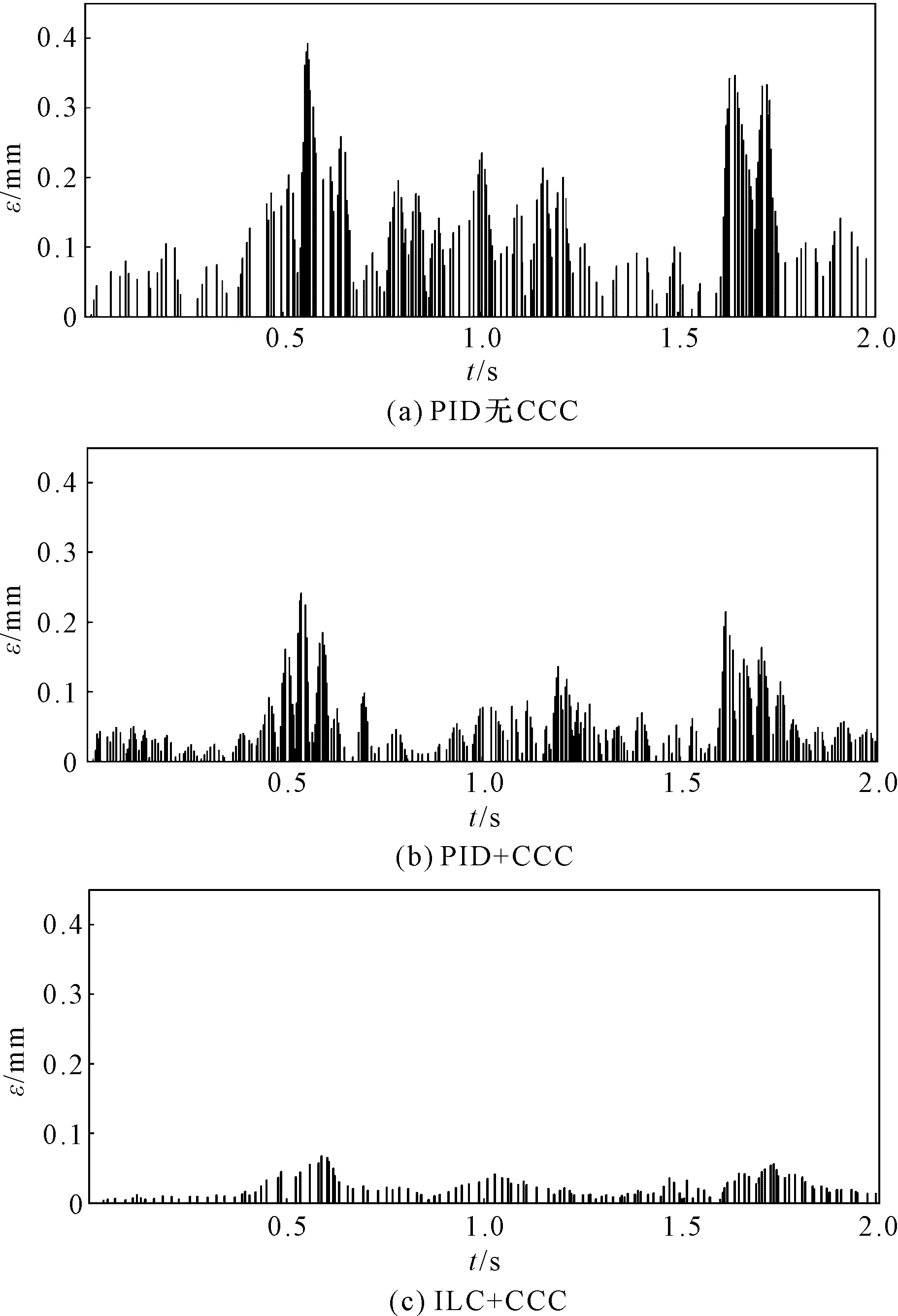
图8 3种控制方法对于理想轨迹产生的轮廓误差

通过图8可以看出：3种控制方法对于轮廓误差的控制效果，从好到差依次为ILC+CCC、PID+CCC、PID无CCC。

在3种控制方法下，三叶玫瑰曲线轮廓误差值如表2所示。

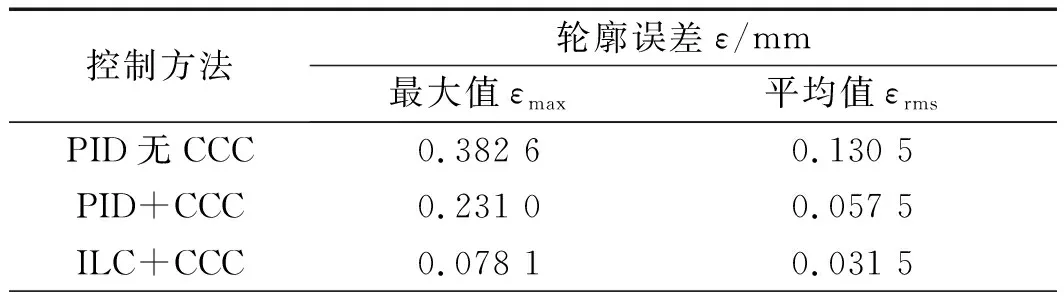
表2 三叶玫瑰曲线轮廓误差值

表2中，给出了轮廓误差性能指标的仿真实验结果。当期望轮廓为三叶玫瑰曲线时，从表2可以得出：采用ILC+CCC控制后，相较于PID+CCC控制和PID无CCC控制，最大轮廓误差分别降低了66.2%、79.5%；平均轮廓误差分别降低了45.2%、75.9%。

在仿真验证中，通过以上图例及数据可以证明，所设计的控制器对于降低轮廓误差具有良好的效果。

4 结束语

本文通过对数控机床进给伺服系统进行研究，设计了变增益交叉耦合迭代学习控制器，用以降低多轴系统轮廓运动控制时的轮廓误差，得到的主要结论如下：

(1)在单轴的位置环设计P型迭代学习控制器，通过对一个复杂函数的曲线进行跟踪分析，证明所设计的控制器可以有效降低单轴的跟随误差；

(2)依据交叉耦合控制原理，结合迭代学习和交叉耦合控制的特点，设计了变增益交叉耦合迭代学习控制器对控制效果进行了改善，解决了在多轴系统进行运动控制时，单纯减小单轴跟踪误差不能保证轮廓误差得到有效抑制的问题；

(3)利用三叶玫瑰曲线作为理想输入轨迹，在MATLAB/Simulink中搭建仿真模型，开展了两轴轮廓控制试验。试验结果表明：所设计的ILC+CCC控制方法相对于PID无CCC控制方法和PID+CCC控制方法，能更有效地提高轮廓加工精度，降低轮廓误差。

但是，由于条件限制，本文只采用了仿真验证，未考虑实际系统中的模型不确定性。在后续的研究中，将借助于实际的试验台，通过实验来验证这方面的结论内容。