一种基于粒子群优化的无键相虚拟动平衡算法研究*

陈立芳，晏资文，李 栋，周 博，郭仪翔，李瑞花

(北京化工大学 机电工程学院，北京 100029)

0 引 言

在高速、高温、高载荷作用下，旋转机械的转子会发生变形、磨损及同心度的变化，使转子由于质心偏离旋转中心引起振动，进而导致整机振动过大。不平衡是旋转机械振动产生的主要原因，其中，质量不平衡引起的振动故障最常见且危害大，需通过动平衡的方法来解决。

在现场动平衡中，大多采用影响系数法。但该方法基于精确的相位检测，且试重一般凭经验进行选取，加上试重条件、测试环境、仪器精度等方面的影响，难以获取准确的影响系数，致使动平衡过程反复，启停机次数增加，影响企业效益[1]。所以在满足平衡要求的前提下，应尽量减少启停机次数，提高动平衡效率[2-5]。

虚拟动平衡法基于有限元法，通过仿真构建与实际转子尺寸和参数相符的有限元模型，在转子配重位置处施加虚拟不平衡激励，对其进行动力学稳态分析。JAlLAN A K和MOHANTY A R[6，7]利用基于有限元技术的仿真模型，成功地检测了转子-轴承系统的故障状态和位置;SHRIVASTAVA A和MOHANTY A R[8]通过建立转子系统的降阶模型，并对转子-盘-轴承系统进行数值模拟，估计了单平面的动平衡参数(幅值和相位角);刘钢旗等人[9]提出了一种基于无试重模态的柔性转子二阶动平衡方法，通过有限元软件进行了建模，对不平衡量进行了逐阶平衡;运侠伦等人[10]建立了主轴转子系统的动力学模型,利用矢量合成原理对配重方案进行了寻优匹配,快速、准确地获取了配重质量和相位;宾光富[11]通过仿真构建了与轴系结构尺寸和运行参数相符的转子动力学有限元模型，分别在各跨转子平衡位置处施加了不平衡激励，计算出了相应的加重影响系数;章云[12]提出了一种高速转子分布式不平衡量无试重识别方法，通过分析比较了扩展影响系数动平衡方法与转子动力学模型,得出了动力学传递函数与影响系数之间的关联关系，并在转子动平衡实验平台上进行了实验，对所提出的方法加以了验证。

近年来，智能优化算法为解决复杂程度的问题提供了一条全新的途径，成为国内外学者关注的研究热点[13]，其思想也逐步应用到了动平衡领域。陈哲超[14]提出了一种基于自适应粒子群优化(APSO)的自动平衡控制算法,结合BP神经网络,实现了一次启停机跟踪后系统的自动平衡控制,并在变速模拟试验台上进行了验证;王星星[15]将一种基于遗传交叉因子改进的粒子群算法，引入到转子动平衡最小二乘影响系数法中，用实例说明了改进后的算法具有很好收敛特性和全局搜索能力,并通过实验验证了该方法的可行性。

以上有关动平衡的研究均需要转子不平衡量的相位信息，因此，该方法对于无法安装键相传感器的场合并不适用。王亚昆[16]提出了一种无需相位信息的动平衡方法，该方法通过两次特殊位置试重，计算出了配重大小及位置；但是该方法求解误差大，实验取得的减振效果仅有11%～32.1%；且其动平衡的精度也较低;吴元东[17]针对存在不平衡量偏大的某型航空发动机，利用3个特殊位置的试重(三圆法)，在无键相传感器的情况下，实现了风扇转子的本机平衡，有效降低了低压转子的振动水平；但利用该方法至少需要启停机5次。

针对某些转子的特殊结构，不具有输出相位信号的条件，又急需进行动平衡的现状，笔者提出一种基于粒子群优化的无键相动平衡算法；在无键相信号的情况下，通过对转子模型进行有限元分析，利用实测的振幅和粒子群搜索寻优技术，只需一次试重便能获得原始不平衡量的大小和位置，大大提高动平衡的精度和效率，最后通过实验对该方法的实用性和有效性进行验证。

1 算法理论基础

1.1 转子动力学理论

根据转子动力学理论，笔者首先建立悬臂双支撑转子的动力学响应模型及运动方程。其中，转子涡动示意图如图1所示。

图1 转子涡动示意图

根据图1的转子涡动示意图，笔者建立轴心O的运动微分方程，即由不平衡质量产生的激振力所引起的强迫振动的微分方程，如下式所示：

(1)

(2)

式中：M—转子系统质量，kg；m—偏心质量，kg；e—偏心距，mm；K—转轴的刚度系数，N/mm；C—阻尼，N·s/mm；Ω—旋转角速度，rad/s；t—时间变量，s；x—水平位移，mm；y—垂直位移，mm。

此处令z=x+iy，并经过欧拉公式变换，其复数形式的运动方程如下：

(3)

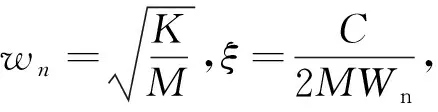
(4)

式中：wn—系统的固有圆频率，Hz；ξ—阻尼比。

其中，wn和ξ只与系统本身参数有关，与初始条件和状态无关。

二阶常系数线性非齐次微分方程(4)的特解可表示为：

z=Aei(Ωt-θ)

(5)

式中：A—不平衡响应幅值，mm；θ—机械滞后角，°。

(6)

式中：λ—频率比。

由式(6)可知，振动响应的幅值仅与不平衡质量和偏心距有关，并与二者的乘积质径积成正比。因此，可以通过减小不平衡质量来减小其振动幅值。

1.2 粒子群基本原理

粒子群(particle swarm optimization， PSO)算法是在鸟类迁徙行为影响下发展起来的一种搜索寻优算法。粒子群中的每个粒子都代表实际问题的潜在解，由位置、速度和适应度值3个指标来表述其特征。适应度是粒子位置的目标函数值，粒子群根据适应度大小来判断粒子位置的优劣[18]，从而计算出个体极值和群体极值，粒子将依据这两个极值，朝适应度指定的方向不断地更新位置和速度，直至找到整个解空间的最优值。其中，个体极值是粒子迄今为止搜索到的最佳位置，群体极值是整个粒子群迄今为止搜索到的最佳位置。

粒子的速度和位置更新的公式为:

(7)

(8)

在搜索优化过程中，W值对算法的收敛性至关重要。当W较大时，全局搜索能力较强；当W较小时，局部搜索能力较好。为了加速收敛而不陷入局部最优，权值W的公式为：

(9)

式中：Wmax—最大权值；Wmin—最小权值；Smax—最大迭代次数。

通过调整，W将随迭代次数s的增加而减小，使粒子前期速度较快，有利于全局搜索；后期速度较慢，有利于局部搜索。

PSO算法具有许多优点，如PSO算法即使从远离最佳位置的起点(初始解)开始寻优，经过很多次迭代，也只需要耗费秒级的CPU时间，就能收敛到最优解。

PSO算法参数表如表1所示。

表1 PSO算法参数表

2 基于粒子群优化的动平衡算法

2.1 粒子群目标函数的构造

为了进行动力学分析，笔者用MATLAB开发了一套基于有限元法的转子计算软件，包括轴系建模、不平衡响应分析、模态分析、坎贝尔图分析等多个模块。经过比对发现，其计算结果与转子轴承动力学分析商业软件dyrobes之计算结果一致，故软件的结果可供粒子群调用。

软件计算流程图如图2所示。

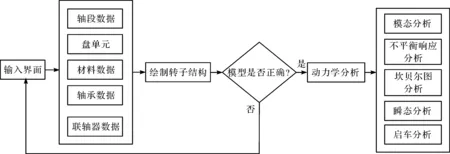
图2 软件计算流程图

笔者在软件中建立与实际转子尺寸和参数相符的有限元模型，用实测临界转速加以校准。一般认为仿真计算的临界转速值与实测值误差在5%以内合理，否则需调整模型参数[19]。建模正确后，通过在模型上添加虚拟激励来进行稳态响应分析，并将整个算法封装成一个函数f(m), 表示在该转子指定状态下，由质量m造成的虚拟振动振幅。由于有限元模型与实际转子非常相似，于是可考虑当两者稳态响应的振幅相等时，模型上的虚拟激励就是实际转子中存在的不平衡量。

按照粒子群算法步骤，可令粒子位置X=[X1,X2,…,X40]T=[m1,m2,…,m40]T，表示待求解的不平衡质量，并将其大小限制在实际要求的范围内；同时，将转子上实测基频振幅A与虚拟振幅的差的绝对值作为粒子群的适应度函数F(m)，如下式所示：

F(mi)=|A-f(mi)|

(10)

在算法中设定：适应度越小，则粒子位置越好。这样一来，粒子位置(不平衡质量)将会朝着适应度减小的方向变化。到算法迭代结束时，F(m)必然得到最小值，一般为纳米级，便可以近似认为A=f(mi)，即：在模型中，找到了一个可以造成振幅A的虚拟不平衡质量mi。由于模型和实际转子高度相似，那这个值可认为就是实际转子中的不平衡质量。这样便能根据实测的基频振幅A来逆向推导，得到转子上造成振幅A的不平衡质量mi。

2.2 不平衡矢量寻优

设初始不平衡质量为m0，相位为β，要实现动平衡，需在(180°+β)的相位上添加与m0大小相同的配重。因此，执行动平衡的首要条件是获得m0和β。

设在某测振截面上用电涡流传感器测取水平方向获取的振动原始信号，对该信号进行FFT变换，然后计算出基频的序号j，则不平衡响应的相位角φ为：

(11)

式中：ImXj—频域信号的第j个虚部；ReXj—频域信号的第j个实部值。

因为没有键相参考，相位角φ只是用来判断不平衡力变化的方向。

设第一次在该截面测的原始振动信号经FFT之后得到的相位角为φ0，提取的基频幅值为A0，则有：

A0=f(m0)

(12)

由前面推导可知，m0可利用粒子群寻优得到。为了获得其确切位置，需要再次启车运行到同一转速，往配重盘上添加一个试重m1，相位为α，笔者直接选取大小为m0的质量作为试重。这时系统总的不平衡量为原始不平衡量m0与试重m1的合成；假设合成后不平衡量是m01，此时同样在该测点处测得振动信号经FFT之后的相位角为φ1，基频振幅为A1，则有：

A1=f(m01)

(13)

以同样的方法，由粒子群寻优得到m01，再由O、m0、m01、m1构成的平行四边形，根据余弦定理得：

(14)

由于余弦函数是偶函数，在[-π,π]范围内的同一函数值对应两个自变量，且两者互为相反数；设余弦函数的解为γ，则有：

α-β=π±γ,β=α±γ-π

(15)

所以根据式(11～15)就可以求解出原始不平衡量m0和相位β。

平衡过程中加重示意图如图3所示。

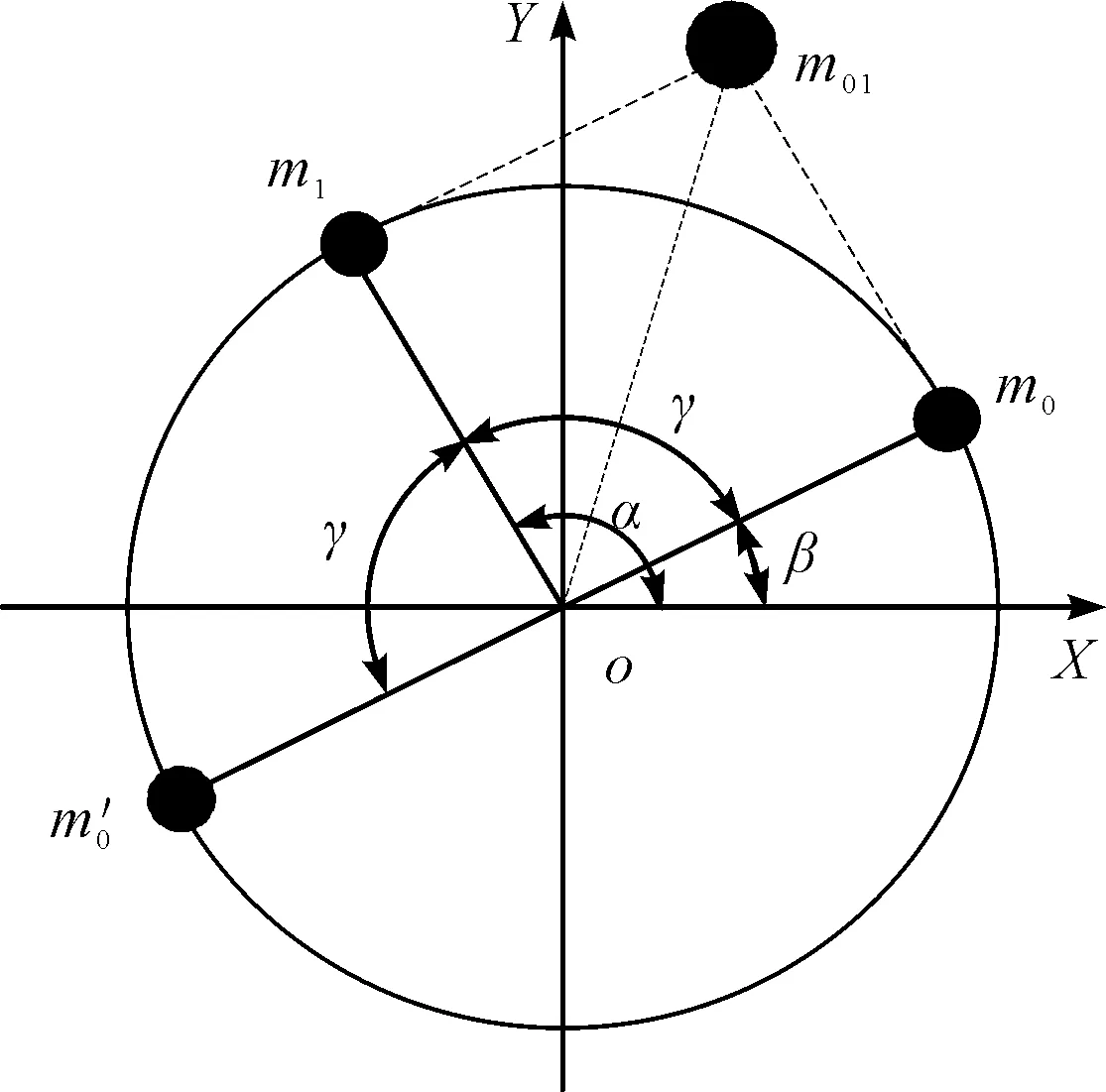
图3 平衡过程中加重示意图m0—原始不平衡质量；m1—试重质量；m01—m1与m0的合成质量；角度为α+γ的配重；α—m1的相位；β—m0的相位；γ—m0与m1的相位差

基于粒子群优化的无键相动平衡算法流程图如图4所示。

图4 基于粒子群优化的无键相动平衡算法流程图

3 仿真分析

该实验所用的是螺旋桨悬臂转子，转子试验台如图5所示。

图5 转子试验台

转子上装有螺旋桨和配重盘，测振箱内装有采集卡和电涡流传感器，采用同步整周期方式来采集振动信号，信号传送至上位机通过软件LabVIEW进行滤波、傅里叶变换，来提取基频数据。

笔者用软件建立与试验台上的转子相似的有限元模型，其具体建模原则如下：(1)配重盘用等质量和惯性矩的盘单元表示，三桨叶螺旋桨按质量、转动惯量等效成盘单元，并且原型与模型的质心在轴上的位置相同；(2)忽略倒角、外螺纹等结构特征；(3)深沟球轴承用两个方向的刚度系数表示；(4)集中质量作用处、轴径变化处、轴承支撑处均保证有支撑节点单元。

根据动力学参数相似、结构相似性等原则，笔者建立的转子有限元模型如图6所示。

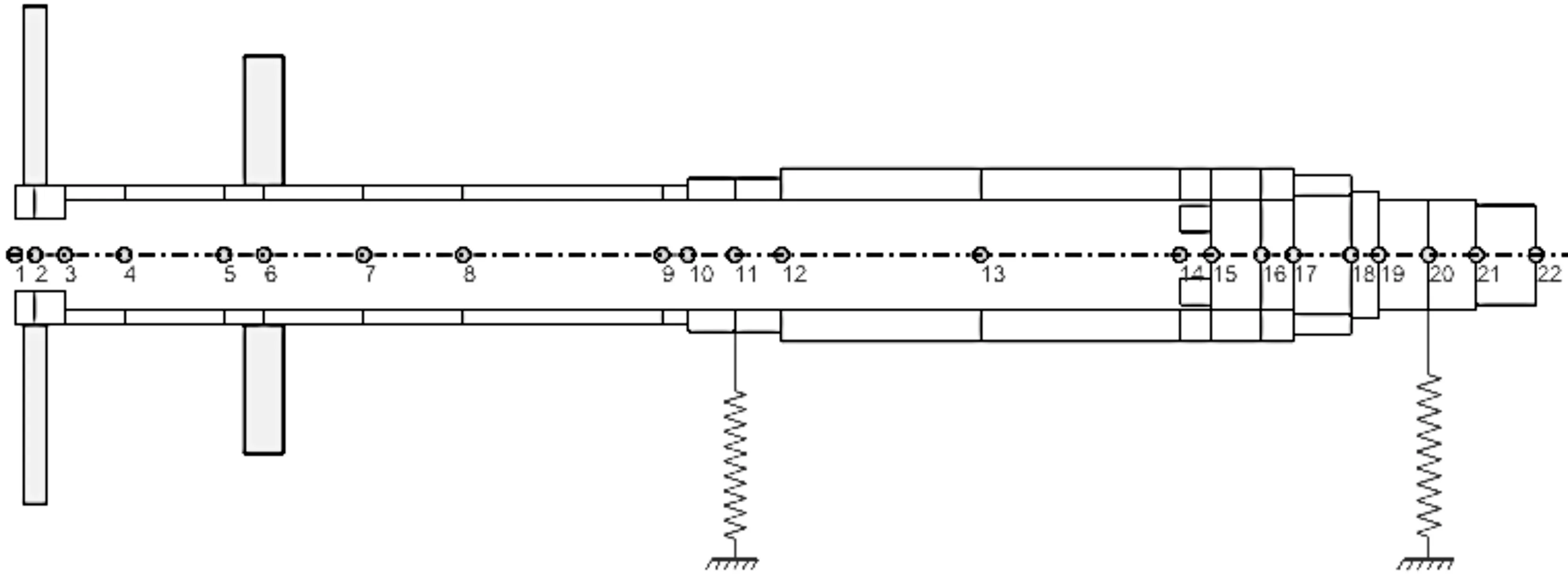
图6 转子有限元模型

同时，笔者进行静态分析，得到两个不同型号的滚动轴承的节点11和节点20处的支反力分别为1 251 N和-519.5 N，利用计算软件，结合该值可近似计算出轴承支撑刚度大小为255 672 N/mm和156 160 N/mm。

支撑刚度计算结果如图7所示。

图7 支撑刚度计算结果

笔者在6节点圆盘0°方向上添加一个60 g·m的不平衡量作为初始激励，假设原先并不知道不平衡量大小和相位，运行软件，利用有限元进行模态分析，得到一阶临界转速为3 830 r/min，然后进行稳态响应分析，由于该转子的振型是端部摆动，将靠近端部的7节点作为测点；将仿真的振动信号经过FFT之后，提取基频振幅为70.8 μm，相位为0°；将这个振幅输入到粒子群中，以原始不平衡量为寻优目标，以式(10)为适应度函数，运行软件，几秒后迭代结束，得到最小适应度f=1.012×10-9m，同时得到粒子的最优解为61 g·m(适应度值随迭代次数增加而减少，说明误差收敛，寻优目标一直朝最优解靠拢)。

与之前的设定值相比，初始不平衡量寻优误差为1.6%。误差较小，可以使用；接着随机在6节点圆盘120°方向添加寻优得到的试重61 g·m，此时再次将7节点振动信号作FFT，得到振幅为70 μm，相位为297°；再次将该振幅代入到粒子群算法中，同理寻优之后根据式(14，15)得到试重与原始激励的相位差刚好为120°，即原始不平衡量相位在0°或在240°方向。经过仿真可知：将6节点处不平衡力的相位变大时，所测振动信号的FFT相位将变小。因此，根据所得FFT相位由0°(360°)变化导297°，便认定添加试重后的总不平衡力往相位增大的方向变化了，所以原始不平衡力必在0°方向；往0°反方向180°添加虚拟配重61 g·m，得到7节点仿真响应2 μm，相比于原始响应减振97%。

通过以上详细的分析可以证明，该方法是完全可行的。

4 实验验证

测试系统流程图如图8所示。

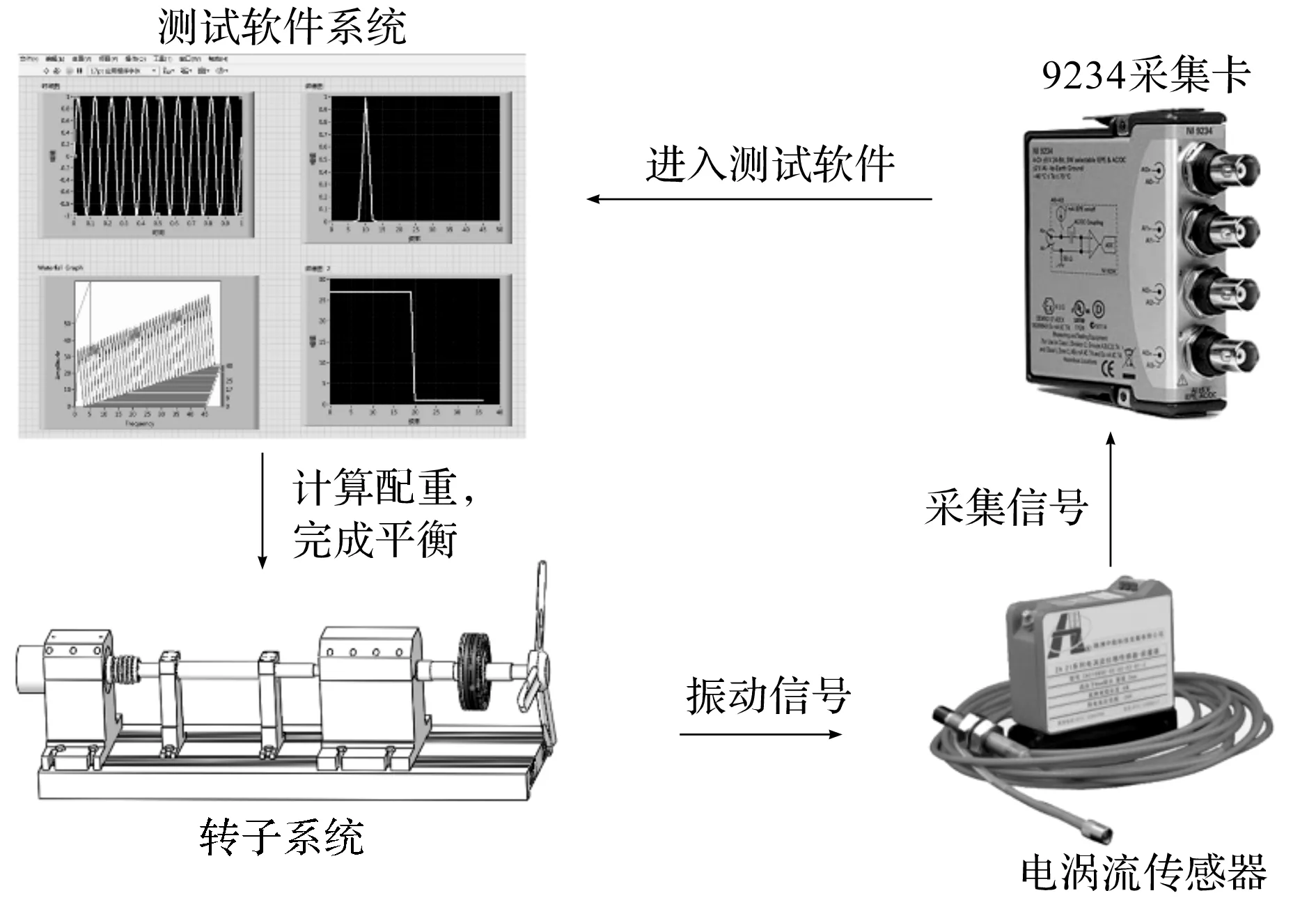
图8 测试系统流程图

由于该悬臂转子进行仿真得到一阶临界转速为3 830 r/min，实验转速选在1 020 r/min。首先在螺旋桨处装上防护罩，启车至4 500 r/min，让转子经过临界转速，根据升速过程中的实测Bode图数据，判断出实际转子一阶临界转速值为3 910 r/min，与仿真模型一阶临界转速3 830 r/min相比，误差2%。由此可以证明笔者所建立的模型是合理的。

现场动平衡的具体步骤如下：

(1)测量原始振动，获得振幅A0和经FFT得到的瞬时相位Φ0；

(2)将A0输入到算法软件，经计算得到原始不平衡质量m0；

(3)添加试重m1，测量此时的振动，获得振幅A1和经FFT得到的瞬时相位Φ1；

(4)将A1输入到算法软件，同理得到m01；

(5)经式(14，15)计算和仿真判断得到原始不平衡m0相对于试重的角度，确定最终配平位置；

(6)添加配重，完成平衡。

实验过程中，把一个20 g的质量块放在0°、120°和240°的位置，与原有残余不平衡量一起作为系统初始不平衡量，共进行3组实验，均在1 020 r/min下进行，0°为配重盘上指定的零点。按上述步骤进行实验，实验中每次先由软件根据初始振动幅值算出不平衡质量，再以同样大小的质量块作为试重进行加重。第一次实验试重48 g，第二次实验试重37 g，第三次实验试重16 g。

记录动平衡实验数据如表2所示。

表2 动平衡实验数据

其中，表2数据为不平衡响应的振幅和瞬时相位，从表2可以看出，随着加重后系统不平衡量的变化，所测到的信号瞬时相位也会相应的增加或减少。

实验中试重和配重信息如表3所示。

表3 试重和配重信息

表3数据为配重与试重的大小和加重位置。

第一次实验时，在平衡前后分别启车过临界，转速升至4 500 r/min，由于过临界时振幅太大，测点变为轴承旁边的12节点，此时测得的平衡前后幅值变化图如图9所示。

图9 平衡前后升速过临界时振动幅值变化图

从图9可以看出，转子的振动明显降低，特别在临界转速附近。由此可以证明所用的配重完全合理，而且只需一次试重就能在无键相的情况下完成平衡。

由于在配重盘上只有12个加重孔，实际操作时并不能按理论计算出来的角度加重，一般是就近原则选择最近的孔位进行配平，即使在这种有误差的情况下，仍然可以实现高效的动平衡，因此，这种方法具有良好的推广情景。

5 结束语

针对转子系统不平衡量引起的振动，本文提出一种基于粒子群优化的无键相动平衡方法；通过对转子系统进行有限元建模，使用实际临界转速优化模型，保证仿真模型高度相似于实际转子；在这种无键相的情况下，一次原始振动测量便能得到不平衡量大小，添加试重后再测一次振动，便能确定不平衡量相位；且试重大小均和配重相等，这样加重时均有一定几率直接平衡，且能保证非常好的平衡效果;经过仿真和实验验证，采用该方法的降振效果可达95%以上。

但该方法需要注意以下几点：

(1)仿真模型需要与实际转子相符，需用实测临界转速来优化和微调模型，直至误差在5%的范围内，且尽可能小，该实验模型临界转速与实测临界转速误差为2%；

(2)该实验转子是一个双支撑单悬臂转子，一般用实测临界转速校准能满足模型精度要求，若遇到多转子等复杂结构、工作转速又过多阶临界的转子，则除了验证实际多阶临界转速外，还要验证振型，并用实际多测点振动数据反复校准模型，直至误差到许可范围；

(3)粒子群算法应注意其收敛性，要选取适当的权值和算法参数，避免陷入局部最优。

总之，该方法内容简单、易于操作，无需安装键相传感器，对动平衡的转子转速范围、测点等都没有特殊限定，可弥补某些旋转机械中无法测量相位的缺点，有较高的工业应用价值。