基于ADAMS与ANSYS的升降机层门联动装置优化研究*

赵秉鑫，卢 宁*，张洪伟

(1.北京建筑大学 机电与车辆工程学院，北京 100032；2.北京理工大学 机械与车辆学院，北京 100081)

0 引 言

升降机的联动装置是升降机智能驾驶系统中的重要组成部分，其主要作用是替代人工手动开关门的操作。联动装置的机架主要用于支撑动力模块、传动模块与导向模块。

为了保证机架在复杂的工况条件下的稳定性，需要机架具有足够的强度和刚度，以确保各个零部件之间保持正确的相对运动和位置关系。当机架的固有频率与激励频率一致时，则会引起共振，产生振动和噪声，降低零部件的使用寿命和传动精度。因此，联动装置机架的合理设计是提高联动装置可靠性的重要保障[1-4]。

联动装置的机架采用台架式结构设计。为了弥补传统设计的缺陷，需要对原有结构进行动态分析，找到原有结构设计的不足之处，然后进行优化设计，以提升机架结构的工艺性。

目前，在对较为复杂的机电设备进行优化设计时，一般采用静力学的方法，即针对研究对象的危险工况进行静力学研究，然后对其进行优化设计，以静力学的分析结果作为最终优化的结果。其中，对于研究对象在外部激励较为复杂的运行状态下，建模过于简化或建立纯刚体模型，会影响对危险工况载荷提取的准确性。因此，对于优化结果的验证，只采用静力学进行分析具有一定的局限性，不能完全验证优化后模型的性能是否满足机电设备正常运行的要求[5,6]。

因此，本文采用ADAMS与ANSYS联合优化设计的方法，对较为复杂的联动装置进行刚柔耦合建模，通过动态分析，得到联动装置的动态特性；利用尺寸优化的方法，对机架进行优化设计，将优化后的模型再次柔性化，进行动态分析，验证优化结果，以达到结构轻量化和减震降噪的目标。

1 联动装置模型的建立

1.1 三维模型的建立

联动装置主要由机架、三相电机、蜗轮蜗杆减速器、圆柱直齿轮、单排链轮、直线导轨与滚珠丝杠螺母组成，其传动简图如图1所示。

图1 联动装置传动简图

此处采用SolidWorks软件，对联动装置的各个零部件进行参数化建模，并且按设计要求进行装配，简化与本次研究无关的零部件，得到简化后的三维模型，如图2所示。

图2 联动装置三维模型

1.2 机架有限元模型的建立

为了获得机架所受到的动载荷，此处将联动装置中的关键零部件通过ANSYS进行柔性化处理，生成相应的MNF文件。由于篇幅有限，此处只给出机架的有限元模型。

机架材料选用Q235-B，泊松比为0.3，弹性模量为210 GPa，密度为7 850 kg/m3。此处采用Solid185单元进行网格划分，共建立了100 984个单元与32 057个节点，一共建立了15个刚性单元区域，将其划分为4部分：第1部分与减速器相连；第2部分与大地相连；第3部分与直线导轨相连；第4部分与丝杠相连，如图3所示。

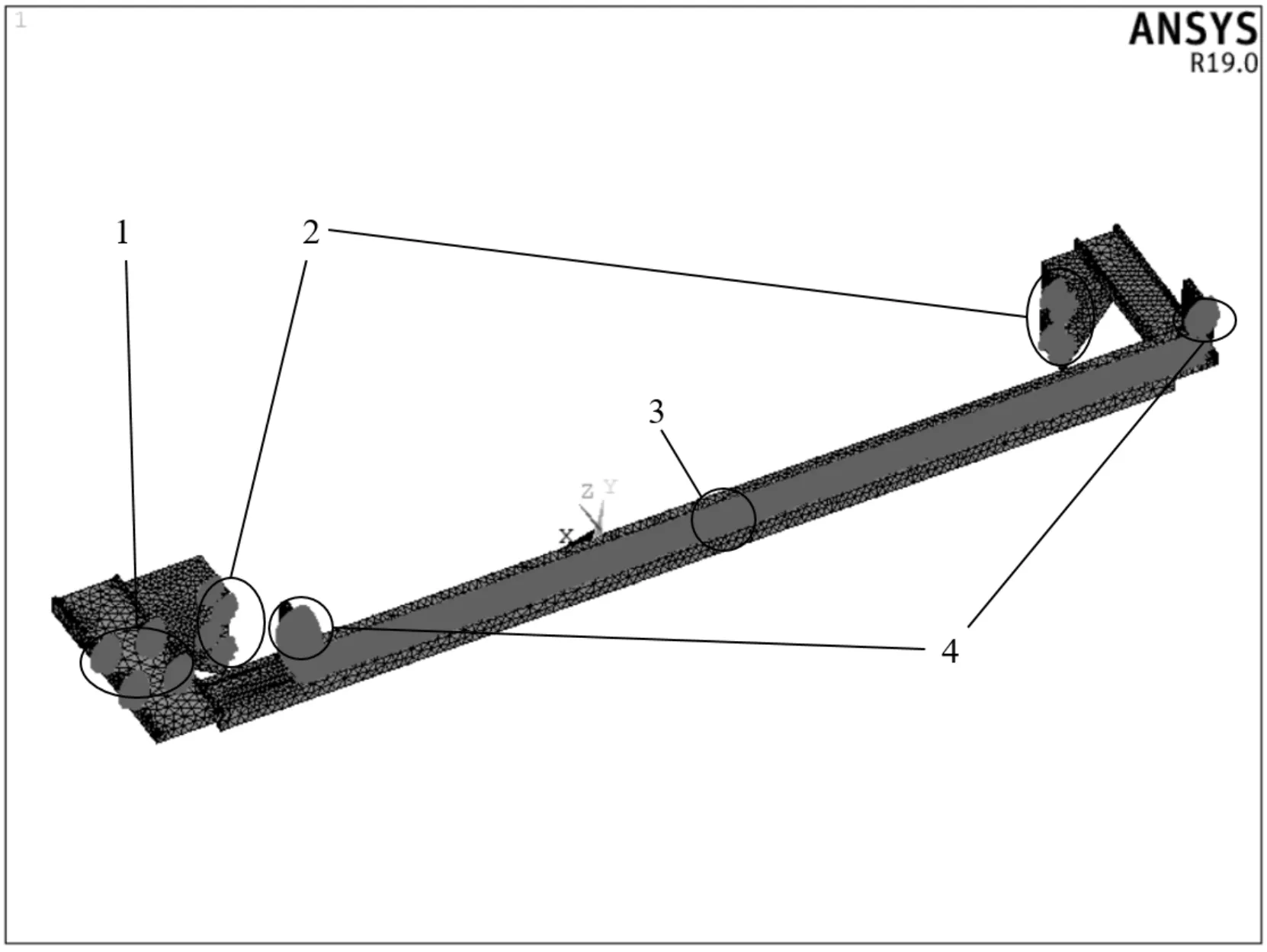
图3 机架的有限元模型

1.3 联动装置刚柔耦合模型的建立

将生成的MNF文件导入至ADAMS中，替换对应的刚体模型，建立刚柔耦合模型[7]；然后为各个零部件之间添加约束。

具体约束关系如表1所示。

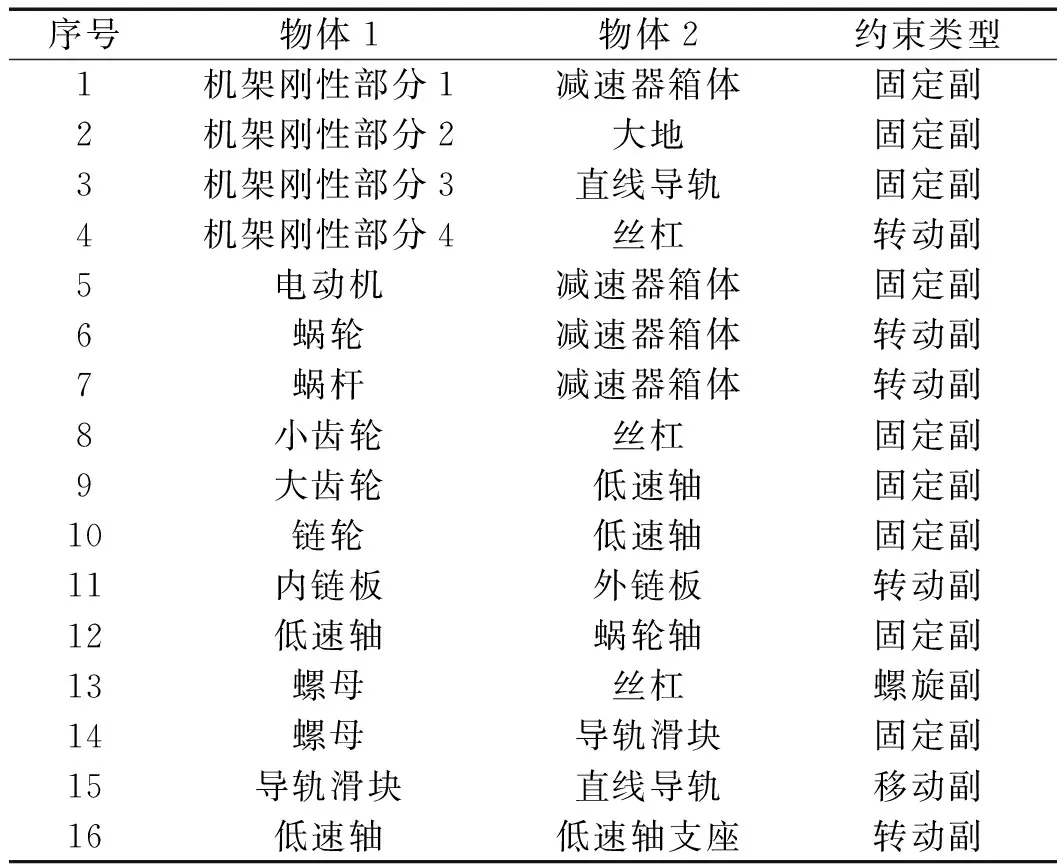
表1 联动装置各零部件间的约束关系

笔者采用ADAMS中的Impact函数，为圆柱齿轮之间、蜗轮蜗杆之间和链轮链条之间添加接触力[8]；根据Hertz接触理论，求得各个传动机构接触的刚度系数[9-11]，并添加相应的阻尼值、力指数与渗透深度；

在蜗杆处添加驱动函数STEP(time,0,0 d,0.1,8 640 d)，模拟电动机的输出转速；在螺母质心处添加沿x正方向的外力STEP(time,0,0,0.1,200 N)和沿y轴负方向的等效扭矩STEP(time,0,0,0.1,50)，模拟打开层门时克服的阻力；在左右2个链条固定零件上，分别添加沿y负方向的150 N外载荷，模拟提升笼门时需要克服的阻力。

完整的联动装置刚柔耦合模型如图4所示。

图4 联动装置刚柔耦合模型

2 联动装置动态特性分析

2.1 模态分析

机架的主要振动激励源是电动机的转频、齿轮啮合激励和蜗轮蜗杆啮合激励，其中，电动机的转频为24 Hz。其他激励频率为：

(1)

式中：n—各零件的转速，r/min；z—齿数。

在稳定工作阶段，齿轮啮合频率为147.97 Hz，蜗轮蜗杆的啮合频率为48 Hz。

为求解出机架更接近实际工况的模态，笔者采用约束模态的分析方法，分析机架的前6阶固有频率[12]。

约束机架左右两端螺栓孔的位移，可得出机架前6阶模态振型图，如图5所示。

图5 优化前机架前6阶模态振型

其前6阶固有频率及振型特征如表2所示。

表2 机架前6阶固有频率及振型描述

对表2结果进行分析可以看出，机架的震动区域主要集中在悬臂部分，机架的1阶固有频率大于电动机的转频，但是与蜗轮蜗杆的啮合频率相近；机架的4阶固有频率与齿轮啮合频率一致，容易产生共振。

可见，为了避免产生共振，需要对机架进行优化设计。

2.2 动力学仿真

笔者设置仿真时间为1 s，仿真步长为100步；将仿真得到ANSYS所需要的FEA载荷文件导入至ANSYS中，进行瞬态动力学分析。

优化前机架的瞬态动力学分析如图6所示。

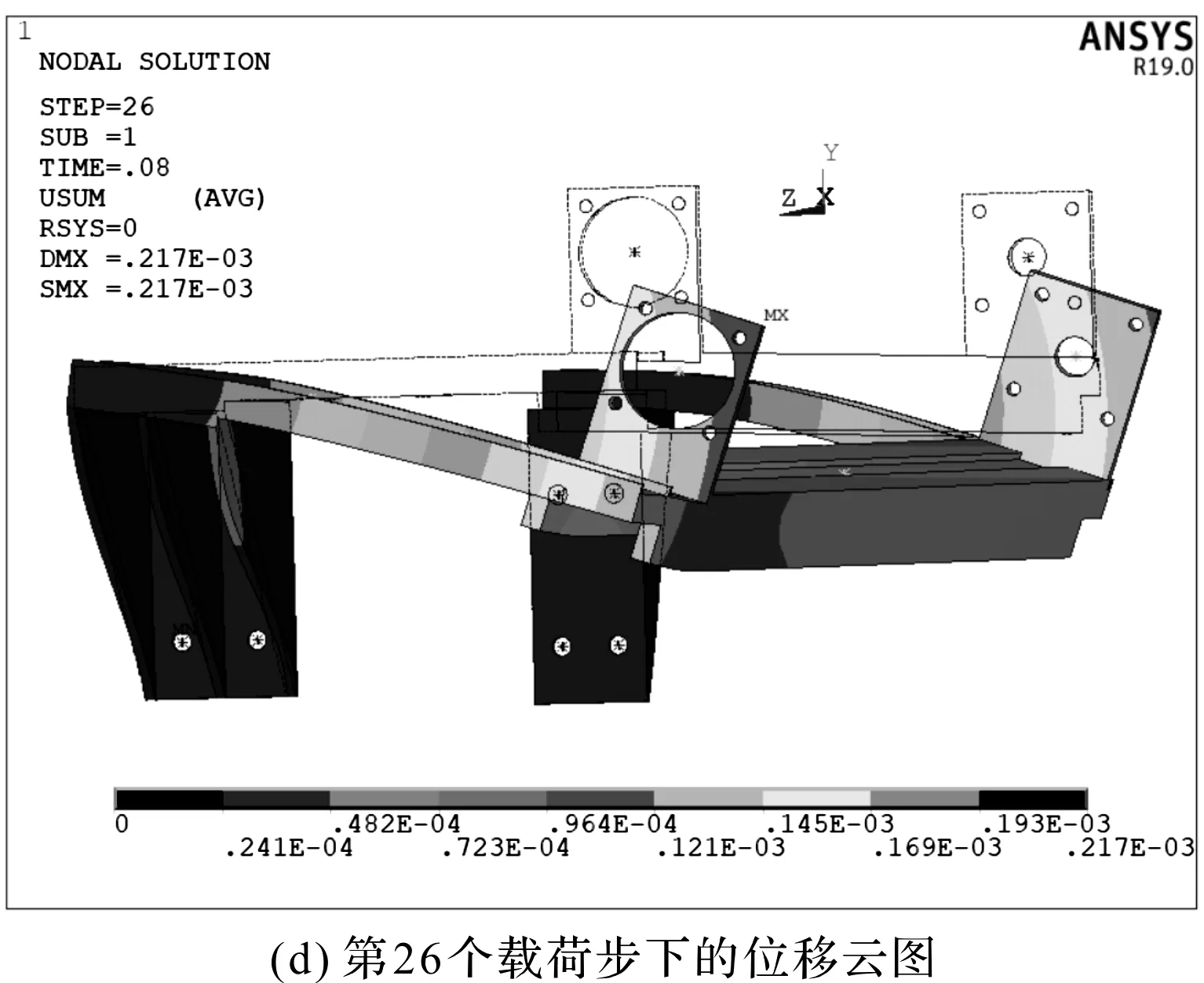
图6 优化前机架的瞬态动力学分析

图6(a，b)中，由于机架主要在Y方向发生变形，通过研究应力与Y方向最大位移随时间的变化曲线可知，在t=0.08 s时刻，机架所受应力最大，机架在Y向位移最大；图6(c，d)则分别为第26个载荷步下机架的等效应力云图和位移云图，最大应力节点位于右侧固定块下部螺栓孔处，数值为97.4 MPa；最大位移出现在机架悬臂位置靠近丝杠固定端处，数值为0.217 mm。

从分析结果可以看出：机架所受最大应力小于材料的许用应力156.7 MPa(Q235的屈服强度为235 MPa，安全系数取1.5)，刚度也满足设计要求。

因此，可在满足刚度强度要求的情况下，通过减少自身重量，提升整体结构的工艺性，避开主要激励频率，对机架进行优化设计。

2.3 载荷的提取

通过瞬态动力学分析可知，在t=0.08 s时刻，机架所受应力最大。导出该时刻的载荷文件，提取出机架与减速器箱体连接处4个外联点的载荷、丝杠连接处2个外联点的载荷、直线导轨连接处1个外联点的载荷，可为优化设计中的静力学分析，提供准确的载荷数据以及作用方向。

在Workbench中施加的载荷如表3所示。

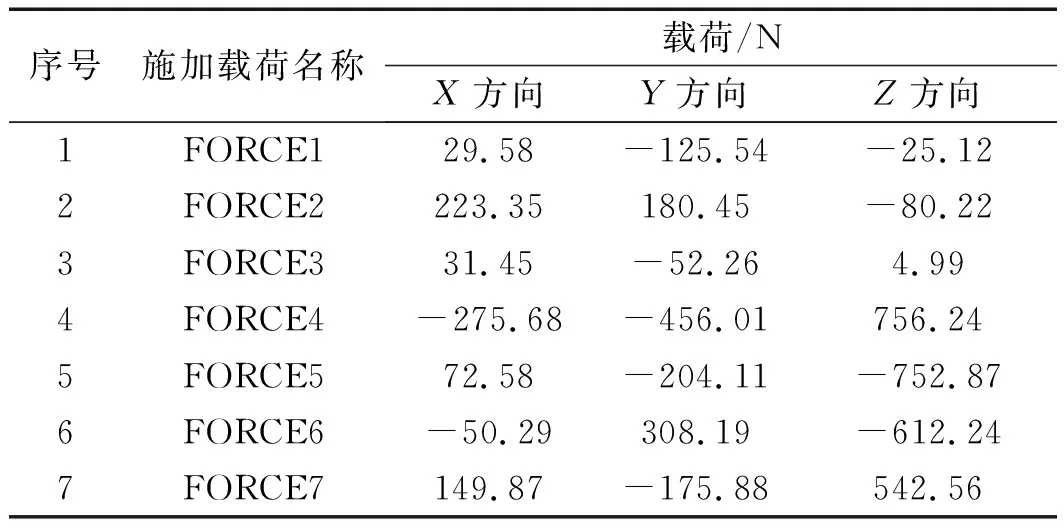
表3 机架外联点的载荷

3 机架多目标优化

3.1 优化数学模型的建立

本次优化以机架的总体质量、最大变形、最大应力、机架的第1阶和第4阶固有频率为目标，将机架各个加强板的尺寸、左右固定块肋板的厚度，以及螺栓孔的相对位置作为设计变量。

机架的三维模型如图7所示。

图7 机架的三维模型

接下来对机架进行优化设计。导入至Workbench的设计变量如表4所示。

表4 设计变量对应关系

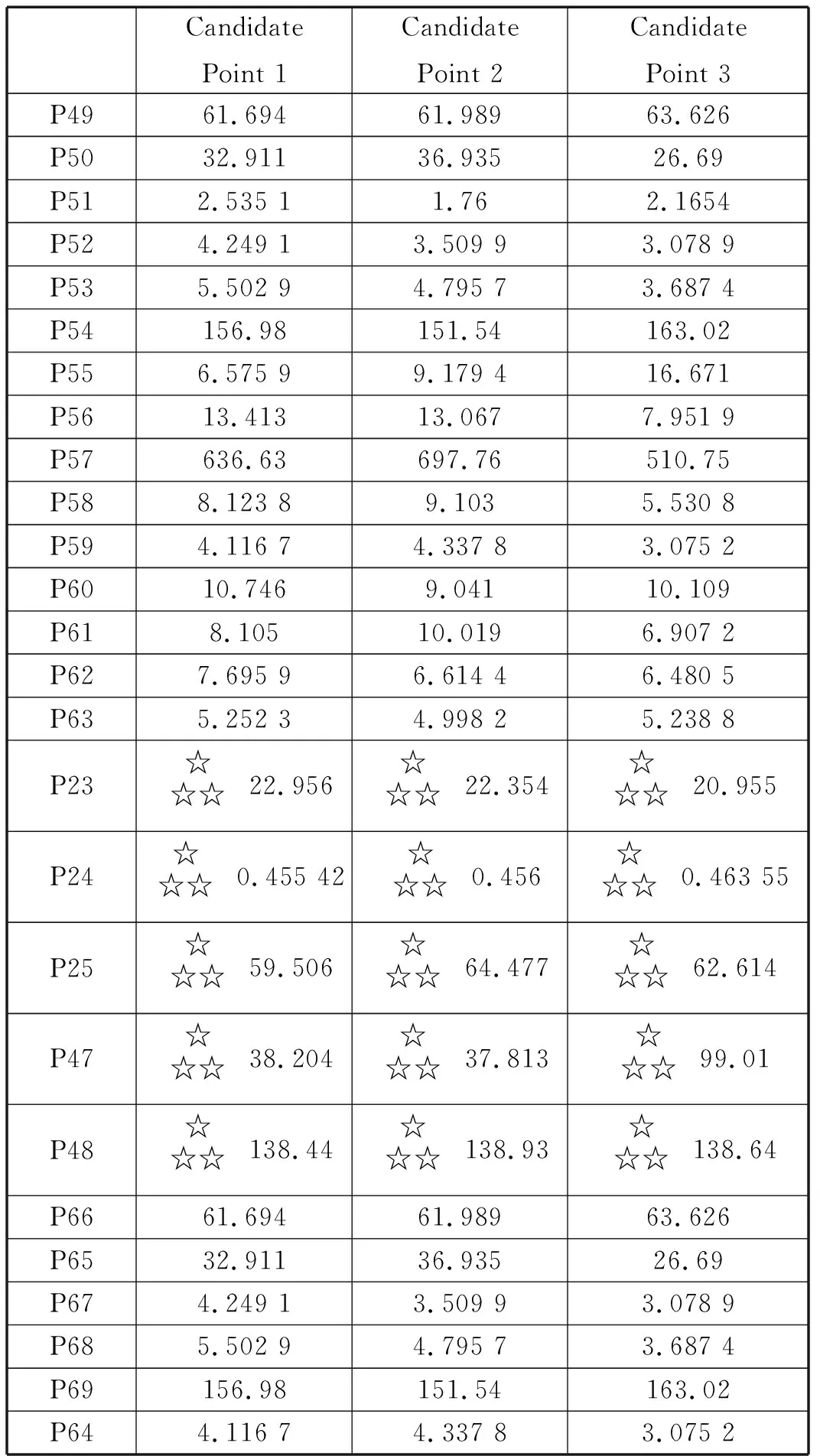
为了便于加工制造，提升其结构工艺性，此处为对称布置的螺栓孔的位置、对称布置的各个加强板与左右固定块厚度及其肋板厚度添加驱动变量，即设计变量P64、P65、P66、P67、P68、P69的输出分别与P59、P50、P49、P52、P53、P54保持一致。

其优化数学模型的目标函数为：

f=min(mass(P),deformation(P),stress(P))

(2)

目标函数的约束条件为：

(3)

3.2 优化过程

笔者对机架左、右固定块的8个螺纹孔添加位移约束，将在动力学分析中所得到的载荷对应添加到静力学模型当中，求解总变形和等效应力。

静力学模型如图8所示。

图8 机架的静力学分析

笔者利用响应面优化设计模块进行优化分析；采用中心复合设计抽样方法(CCD)进行实验设计，生成了150个试验点，根据生成的设计点进行响应面分析，可以得到每个独立输入参数对每个输出参数之间的关系[13]。

依据Kriging响应面模型对机架总质量、最大变形、最大应力、机架第1和4阶固有频率的拟合关系，可判断生成的响应面模型计算值与CCD求得的设计值之间的对应程度，如图9所示。

图9 基于Kriging函数的响应面模型拟合度曲线

笔者插入一个真实的设计点验证模型的可靠性，结果显示，图中机架总质量、最大变形、最大应力以及第1和4阶固有频率所对应的点，都在对角线附近；该响应面模型对总质量、最大应力、机架第1和4阶固有频率的拟合程度优于最大变形，但对各个参数的拟合误差均小于10%，满足后续设计分析的需求。

设计灵敏度反映了输入变量的改变对目标函数变化的影响程度，其本质为输出变量对于各输入变量的偏导数[14，15]。

各设计变量对目标函数的灵敏度如图10所示。

图10 输入变量对输出变量的灵敏度系数

质量对应输出变量P23，各个设计变量与质量正相关，其中，滑台支撑板的高度对质量影响最大，前侧加强板1和2的尺寸对质量影响次之，且均成正相关；

变形对应输出变量P24，前侧加强板2的高度对变形影响最大，滑台支撑板的高度、左侧加强板的高度与前侧加强板1的高度对变形的影响较为突出，且均成负相关；

应力对应输出变量P25，螺栓孔的Y向布局、右侧固定块的各个变量对最大应力成负相关，前侧加强板2的高度与宽度、前侧加强板1的高度和滑台支撑板高度对最大应力成正相关，且滑台支撑板高度对应力影响最大；

1阶固有频率对应输出变量P47，前侧加强板1和2的高度对机架1阶固有频率影响最为突出，成正相关；

4阶固有频率对应输出变量P48，右侧固定块肋板的厚度、前侧加强板2的高度与左侧加强板的高度与对机架4阶固有频率成正相关，滑台支撑板的高度对机架4阶固有频率影响最大，成负相关。

笔者对Kriging响应面模型进行迭代计算，得到3个候选方案，如图11所示。

CandidatePoint 1CandidatePoint 2CandidatePoint 3P4961.69461.98963.626P5032.91136.93526.69P512.535 11.762.1654P524.249 13.509 93.078 9P535.502 94.795 73.687 4P54156.98151.54163.02P556.575 99.179 416.671P5613.41313.0677.951 9P57636.63697.76510.75P588.123 89.1035.530 8P594.116 74.337 83.075 2P6010.7469.04110.109P618.10510.0196.907 2P627.695 96.614 46.480 5P635.252 34.998 25.238 8P23☆☆☆22.956☆☆☆22.354☆☆☆20.955P24☆☆☆0.455 42☆☆☆0.456☆☆☆0.463 55P25☆☆☆59.506☆☆☆64.477☆☆☆62.614P47☆☆☆38.204☆☆☆37.813☆☆☆99.01P48☆☆☆138.44☆☆☆138.93☆☆☆138.64P6661.69461.98963.626P6532.91136.93526.69P674.249 13.509 93.078 9P685.502 94.795 73.687 4P69156.98151.54163.02P644.116 74.337 83.075 2

综合以上分析可知，对于各设计变量的优化优先级，依次是：滑台支撑板高度、前侧加强板1和2的尺寸、右侧和左侧固定块的尺寸、右侧和左侧加强板的尺寸、螺栓Y向布置尺寸。

考虑到结构的工艺性与加强板的常用尺寸，可得到最终优化设计尺寸，如表5所示。

表5 优化前后尺寸对比

3.3 优化结果对比与验证

考虑到机架外部激励复杂，静力学不能满足校核的标准，故此处根据优化后的尺寸对机架重新建模，进行刚柔耦合动力学分析。

优化后机架的瞬态动力学分析如图12所示。

图12 优化后机架的瞬态动力学分析

图12(a，b)中，通过分析优化后模型的应力与Y方向最大位移随时间的变化曲线可知，在t=0.51 s，机架所受最大应力为88.5 MPa，应力最大节点位置未发生改变，如图12(c)所示；在t=0.04 s，其最大变形为0.158 mm，变形最大位置也未发生改变，如图12(d)所示。

通过刚柔耦合动力学分析知，机架在启动加速至稳定运行阶段内所受的应力减少了8.9 MPa，小于材料的许用应力；最大位移减少了0.059 mm，满足设计要求；机架的总质量由26.5 kg下降至19.5 kg，减少了28.3%；

本次优化包括对机架的1和4阶固有频率，但其优化结果不能完全保证机架的固有频率与激励频率错开，可能发生其中几阶频率之间次序互换的现象[16]，故通过约束模态再次分析，结果显示优化后的机架固有频率都有降低，避开了主要激励频率。

优化结果对比如表6所示。

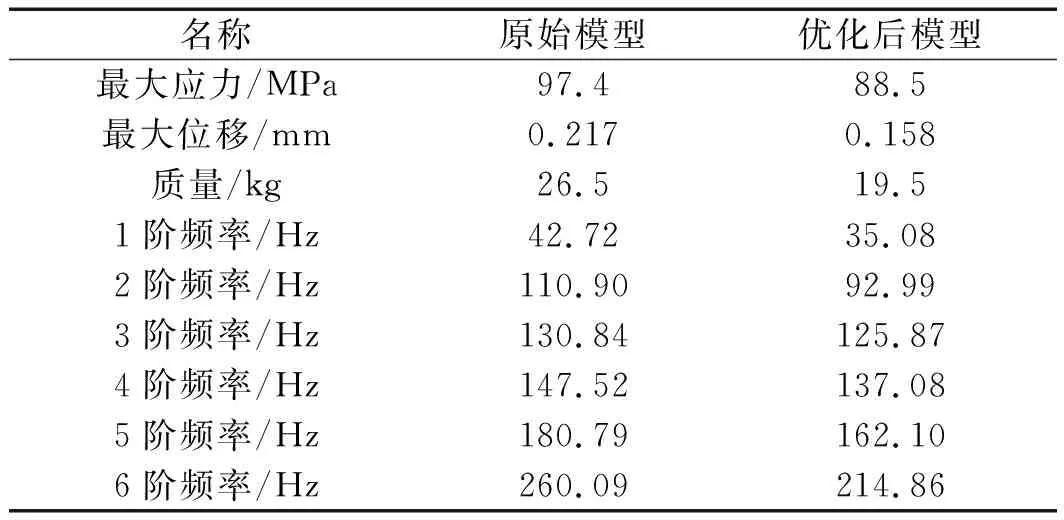
表6 优化结果对比分析

4 结束语

针对某SC型升降机联动装置的机架，本文采用ANSYS与ADAMS联合优化的方法，进行了结构优化设计，主要过程和结论如下：

(1)为了得到机架真实的工况，在ADAMS中建立了联动装置的刚柔耦合模型，通过对机架的动态分析，得到了机架的前6阶固有频率以及联动装置在启动加速至稳定阶段内机架的最大应力与最大变形；分析结果表明，机架的强度与刚度均满足设计要求，可以进行优化；机架的1阶与4阶频率与激励频率相近，需要进行优化；

(2)采用ANSYS对机架进行尺寸优化，建立了响应面预测模型，分析了输入参数与输出参数之间的关系，通过求解得到了设计参考点。

优化结果显示：在保证机架结构强度与刚度的前提下，其前6阶固有频率均有所降低，避开了主要激励频率；机架的总质量减少了7 kg，与原有结构相比降低了28.3%，提升了结构的工艺性，降低了制造成本，弥补了经验设计的不足，为后续的生产制造提供了理论依据。