菱形HSLDS隔振器负刚度机构质量及摩擦力影响分析
袁屹杰,纪 明,张卫国,伊兴国,王 毅,施道云
(西安应用光学研究所,陕西 西安 710065)
引言
随着光电传感器性能的逐渐提升,对平台隔振的需求也越来越严格[1]。传统线性隔振器仅能有效隔离频率大于倍自身谐振频率的扰动,在一些扰动频率较低的应用中,为了满足隔振需求,隔振器刚度需要降低至容易导致失稳的水平。而HSLDS 隔振器[2]则较好地解决了上述问题,在维持一定静刚度的前提下,通过非线性调节,可以降低动态刚度,甚至达到“准零刚度”(QZS)状态[3],具备良好的应用前景,已成为行业的研究热点。
目前,HSLDS 隔振器的多数研究聚焦于负刚度机构理论研究层面,提出了多种负刚度机构形式[4-11],对负刚度机构的几何参数、弹性器件参数进行了充分分析。部分研究涉及了非线性隔振下摩擦力直接作用于负载的特性[12-13]以及几何非线性摩擦力对隔振的影响[14],但鲜有研究分析负刚度机构的质量及内部摩擦力对隔振的影响。在一些应用中,如采用连杆形式的负刚度机构(特别是多层连杆结构[10]),内部运动环节较多,摩擦力因素影响较大,并且隔振过程中,负刚度机构也关联地运动,自身质量的影响难以忽视,否则将导致理论分析与实际存在较大差异,不利于指导实践。
针对上述问题,本文以一种具有较灵活刚度非线性调节能力的菱形连杆负刚度机构HSLDS 隔振器(简称菱形HSLDS 隔振器)为目标,采用虚功法建立负刚度机构等效摩擦力数学模型,构建隔振器拉格朗日方程,并采用谐波平衡法[15]求解,分析负刚度机构的质量及摩擦力因素对隔振的影响。
1 隔振器建模
菱形HSLDS 隔振器如图1 所示,由圆周均布的4 组菱形负刚度机构与包含4 个主隔振器的传统隔振平台并联构成。菱形连杆机构的拉簧处于拉伸状态时,菱形连杆机构产生负刚度效应。

图1 菱形HSLDS 隔振器Fig.1 Rhombic HSLDS vibration isolator
1.1 摩擦力建模
为便于分析,本文仅考虑动库伦摩擦,忽略粘滞摩擦影响,同时仅考虑由拉簧产生正压力导致的铰接副摩擦力,忽略铰接副由端面及径向扭转导致的摩擦力,并假定摩擦系数不受外力影响,且A、C处铰接轴不存在绕其轴线的转动,B、D处铰接轴相对于BD连线不存在转动,如图2 所示。当4 组负刚度机构共同作用时,依据虚功定理存在以下关系:

式中:M1、M2为摩擦力矩;F为负刚度机构在振动方向的等效摩擦力;h>0,即图2 所示状态,在(1)式取上端符号,反之取下端符号。依据设定有:M1=f1µr、M2=f2µr,其中f1、f2为连杆压力, µ为接触面摩擦系数,r为铰接轴半径。根据几何关系:

(1)式可化为

依据几何及受力关系,由(2)式可推导出:

式中f为负刚度机构拉簧的弹性力,且又有:
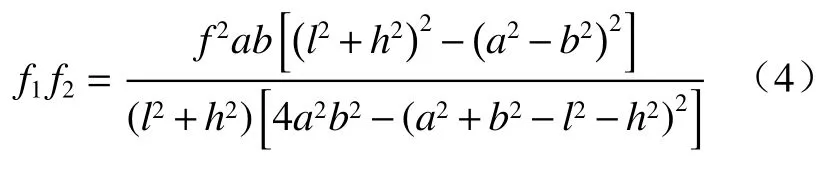
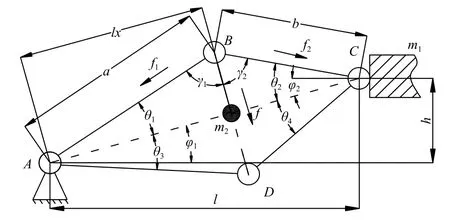
图2 菱形负刚度机构分析图示Fig.2 Schematic diagram of rhombic negative stiffness mechanism
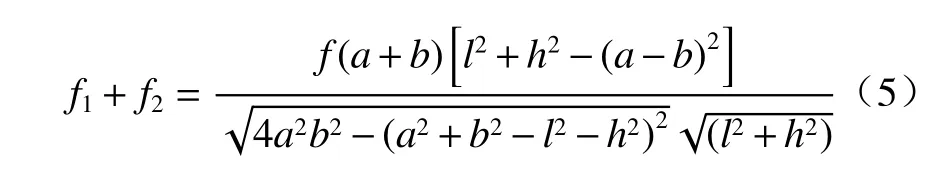
联立(3)式~(5)式,令f=k2Δ,可得:
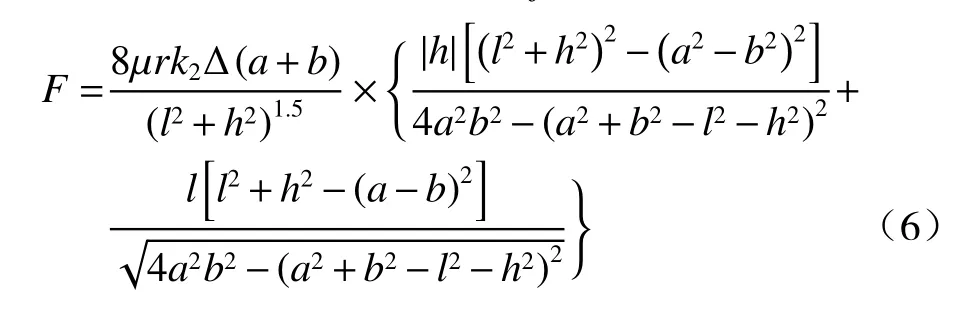
式中:k2为拉簧刚度;

式中dki为菱形HSLDS 隔振器处于平衡位置(即图2中h=0)时负刚度机构拉簧的预拉伸量。
利用ADAMS 虚拟样机对等效摩擦力模型进行验证,如图3 所示,仿真数据与计算数据吻合得较好,表明模型是正确的。
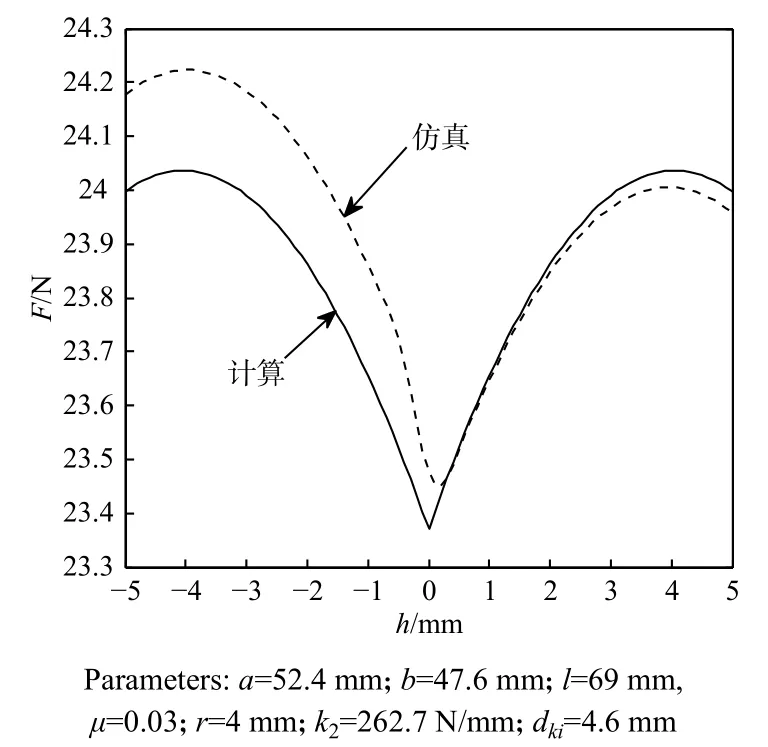
图3 负刚度机构等效摩擦力验证Fig.3 Verification of equivalent friction of negative stiffness mechanism
1.2 动力学方程建模
隔振装置中运动部件质量主要分为有效载荷m1以及负刚度机构质量m2两部分。为简化分析,将负刚度机构视为集中质量。考虑到拉簧组件及其配合的铰接轴是负刚度机构质量的主要构成部分,可将质心设定在图2 中中点位置处。
依据拉格朗日方程有:

式中L=T−V,其中
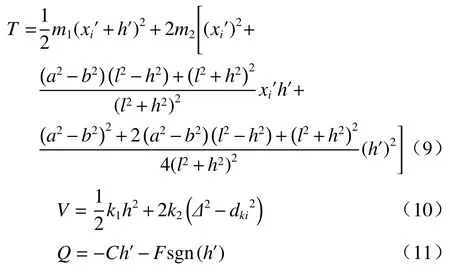
(9)式中xi为施加至振动基座的扰动位移,(10)式中k1与(11)式中C分别为主隔振器的刚度和与阻尼系数和。
将(9)式~(11)式代入(8)式中,得:

式中相关因子及其泰勒级数简化见(13)式~(18)式,泰勒级数取至第3 阶。
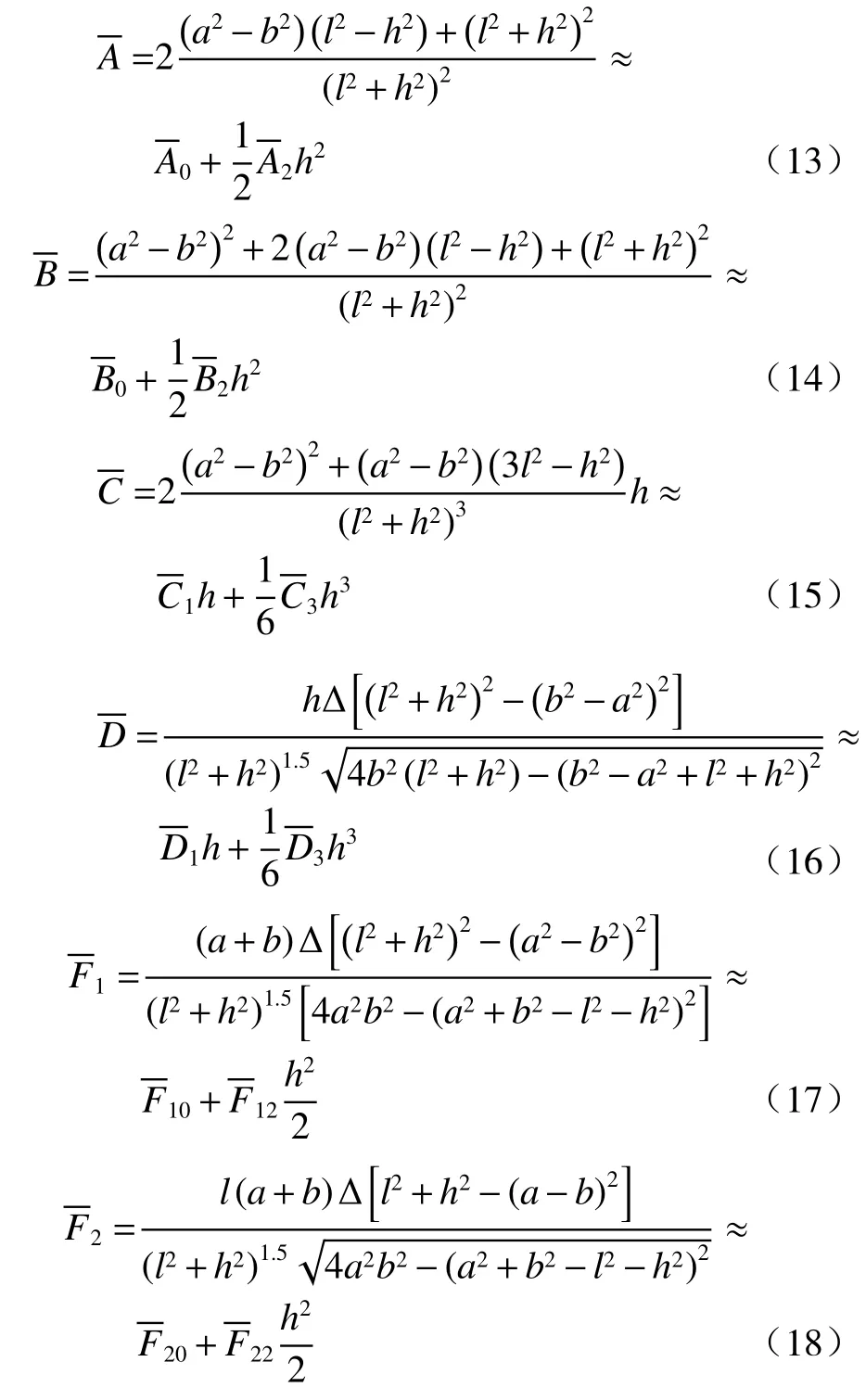
泰勒级数中符号的含义为:X0=X|h=0,X1=依此类推。
由(7)式、(16)式~(18)式可知,负刚度拉簧的预拉伸量dki与负刚度机构等效摩擦力及隔振器等效刚度参数存在密切关系。为使分析更为直观,引入零位刚度概念,即:


式中α=k2/k1。
1.3 动力学分析方法
本文以绝对位移传递率作为隔振性能评价参数,采用谐波平衡法求解动力学方程。令输入绝对位移为输出相对位移分别为cos(ωt+φ)。
使用傅里叶展开对符号函数sgn(h)及sgn(h′)进行简化[14]:


式中:

动力学方程存在以下幅频关系:

则隔振装置的绝对位移传递率为

2 参数分析
首先,设定如表1 所示的一般性参数。

表1 分析参数Table 1 Analysis parameters
2.1 摩擦力特性分析
联立(6)式、(7)式和(20)式,等效摩擦力分析数据如图4 所示。由图4 可知,在隔振运动过程中,等效摩擦力变化幅度较小,在限定及摩擦系数的条件下(后续分析均基于此限定),负刚度机构的几何参数决定了铰接副的受力情况,对等效摩擦力影响较大,即基准尺寸l一定时,杆长a、b与平衡位置处等效摩擦力呈正相关关系,见图4中序号A、B、C;较长杆较短时,增大两连杆长度的差值(后简称杆长差),平衡位置处等效摩擦力减小,见图4 中序号B、D;较长杆较长时,随着杆长差增大,平衡位置处等效摩擦力呈现先减小后增大的趋势,见图4 中序号C、E、F。显然,等效摩擦力受杆长几何因素的影响,存在2 个临界值,即由杆长差导致的平衡位置处等效摩擦力变化趋势开始发生改变的较长杆杆长临界值,以及较长杆大于杆长临界值时,平衡位置处等效摩擦力开始大于连杆等长情况的杆长差临界值。受篇幅限制,对此本文不展开分析。

图4 等效摩擦力几何非线性分析Fig.4 Equivalent friction geometric nonlinear analysis
2.2 隔振性能分析
负刚度机构质量对隔振的影响如图5 所示。由图5 可看出,随着 β增加,即负刚度机构质量增加,将导致谐振点频率降低,位移传递率增加,同时还会提升高频段的位移传递率,如图5 中曲线A、B。
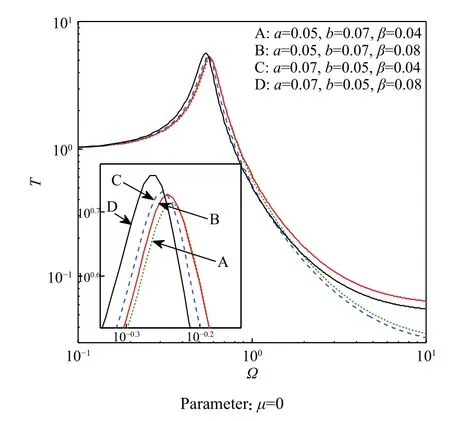
图5 菱形负刚度机构质量影响分析Fig.5 Analysis of mass effect on rhombic negative stiffness mechanism
此外,当负刚度机构连杆不等长,且与载荷平台铰接的连杆较短,即负刚度机构的质心偏向载荷平台一侧时,在较高频段的位移传递率低于质心偏向振动基座一侧的情况,如图5 中曲线B、D。
负刚度机构摩擦力对隔振性能的影响与阻尼类似,减小低频段位移传递率,增大高频段位移传递率,如图6 中B1、B2。菱形HSLDS 隔振器可以通过增加负刚度连杆机构的杆长或杆长差方式,对刚度非线性进行设置,实现隔振优化,如图6 中A1、B1、C1。当摩擦力因素不可忽视时,增加杆长将增大等效摩擦力,在优化低频隔振性能的同时,导致高频隔振性能下降,如图6 中A2、B2;利用杆长差方式进行调节且同时满足刚度非线性优化与降低摩擦力条件时,增加杆长差可降低谐振点频率,改善较低频段隔振性能的同时,减小摩擦力对高频隔振的不利影响,如图4 中B、D 与图6 中B2、C2。

图6 菱形负刚度机构摩擦力影响分析Fig.6 Analysis of friction effect on rhombic negative stiffness mechanism
3 实验验证
3.1 实验分析方法
受实验条件限制,选用两组规格的负刚度机构,分别对负刚度机构质量因素以及摩擦力因素进行实物测试,通过与计算结果对比,验证建模的准确性,并以此保证分析结果的合理性。
测试中,组Ⅰ负刚度机构杆长分别为60.3 mm、49.2 mm;组Ⅱ负刚度机构杆长分别为52.4 mm、48.2 mm。所有铰接副采用柔性轴套与钢轴配合方式。第1 组实验:在润滑条件下,通过对调组Ⅰ负刚度机构与振动基座及载荷平台的连接关系,分析负刚度机构质心位置对隔振性能的影响;第2 组实验:通过改变组Ⅱ负刚度机构铰接副接触面的润滑状态,分析负刚度机构内部摩擦力对隔振的影响。为确保计算符合实际,计算中的主要物理数据通过实测方法获得。
3.2 实验数据
采用图7 所示摩擦力矩测试环境,对不同受力情况下有、无油脂润滑的铰接副接触摩擦力矩进行测试,得到图8 所示的摩擦系数曲线,其中AS1、AS2 分别对应2 个柔性轴套样本。
通过测量,得到菱形HSLDS 隔振器处于平衡位置时,组Ⅰ、Ⅱ负刚度机构拉簧的拉力分别为789 N、1029 N。通过受力分解,计算得出此时负刚度机构连杆的受力f1、f2,如表2 所示。由于连杆分力的差值不大,根据图8 摩擦系数变化趋势,可假定各组计算中摩擦系数是固定的,摩擦系数取值见表2。其他参数依据测试环境取:m=12 kg,l=70 mm,输入扰动加速度幅值G=1.4 g,并设定ξ=0.075。依据表2 中数据,通过动力学解算得到图9 所示传递率计算曲线,对应实物测试传递率曲线如图10 所示。图9 和图10 中,序号0 皆为主隔振器隔振传递率曲线,且序号1~4 曲线分别与表2中序号1~4 数据相对应。计算与实测曲线的谐振点参数如表3 所示。其中序号0 谐振峰值的计算传递率与实验传递率基本一致,表明主隔振器的计算阻尼与实际是相符的,在此基础上序号1~4 的计算与实验谐振峰值数据吻合得较好。在较高频部分,对比不考虑负刚度机构自身因素的计算数据,本文提出的计算模型大幅提高了传递率的准确度,与实验数据具有较高的相符性,如表4所示。同时还可观察到,序号1 在较高频部分(如30 Hz 与50 Hz)的传递率略低于序号2,这与理论分析结果一致;但润滑状态的序号3 在较高频的传递率反高于非润滑状态的序号4,这与逻辑分析结果相悖,分析其原因与采用的润滑方式有关。在较高频段,转动副的相对转动位移量较小,受润滑脂的粘滞效应影响导致实际摩擦系数增大,因而产生与理论分析结果不符的现象。

图7 摩擦力矩测试环境Fig.7 Friction torque testing environment
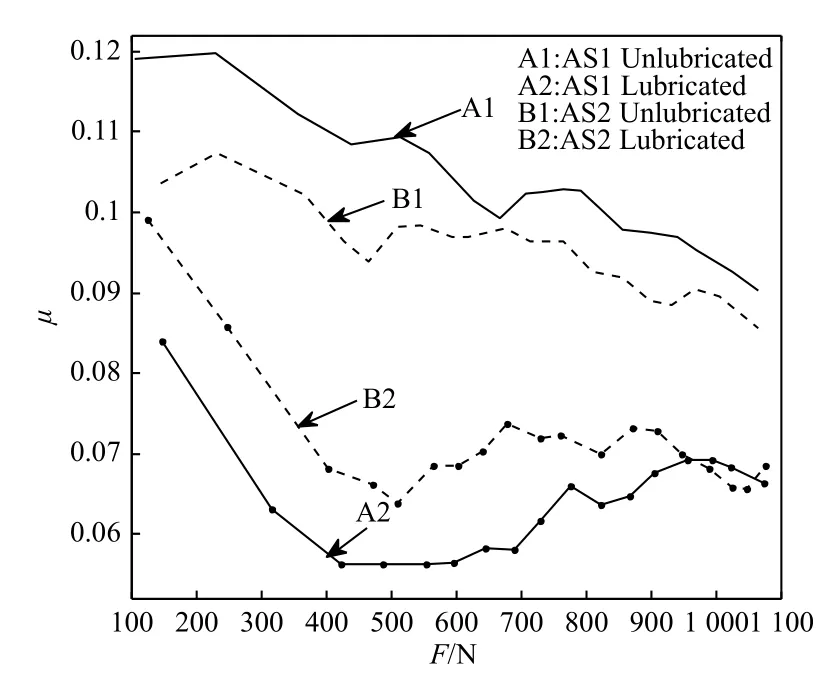
图8 柔性轴套-钢轴摩擦系数图Fig.8 Friction coefficient diagram of flexible sleeve-steel shaft

表2 负刚度机构实验参数Table 2 Experimental parameters of negative stiffness mechanism

图9 隔振传递率计算曲线Fig.9 Calculation curves of vibration isolation transmissibility


图10 隔振传递率实验曲线Fig.10 Experimental curve of vibration isolation transmissibility

表3 谐振点参数Table 3 Resonance point parameters
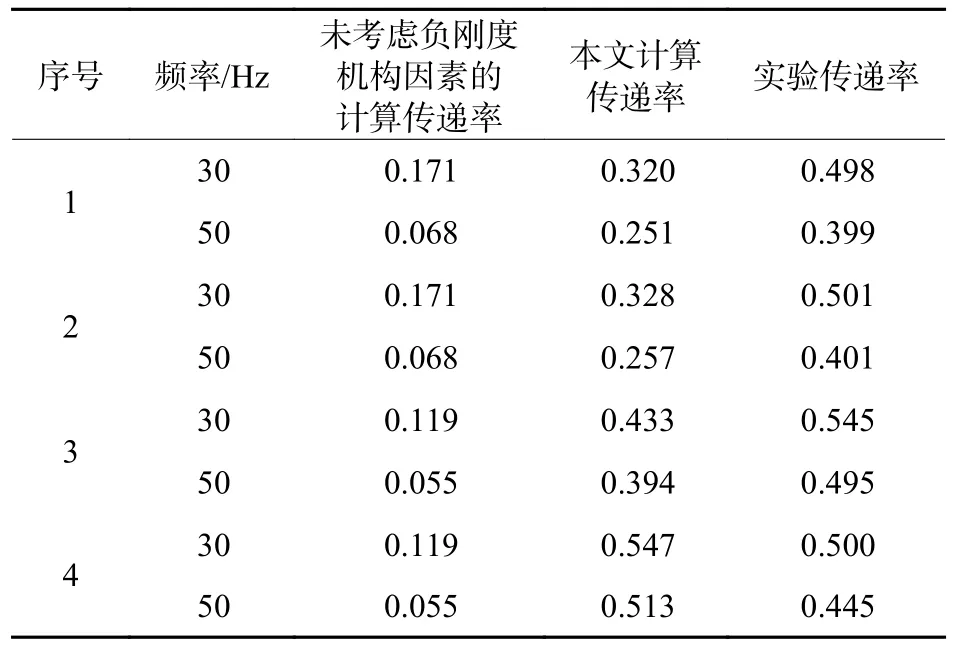
表4 较高频率段参数Table 4 Parameters of higher frequency band
4 结论
针对菱形HSLDS 隔振器,对负刚度机构的等效摩擦力进行建模,将负刚度机构的质量、摩擦力因素纳入动力学方程,并通过实物测试验证了上述数学模型的准确性。得出以下结论:
1) 增加负刚度机构质量对低频段隔振的影响与增加有效负载情况类似,同时会恶化高频段隔振性能,在隔振器设计中应尽量减小负刚度机构的质量;当负刚度机构质量一定且连杆不等长时,可将较短连杆的一侧、即质心偏向侧,铰接于载荷平台,以减小负刚度机构质量对高频段隔振性能的影响。
2) 负刚度机构铰接副摩擦力对隔振的影响与阻尼类似,应尽量减小负刚度机构铰接副摩擦力。当摩擦系数难以充分降低时,在隔振刚度要求一定且摩擦系数受外力影响较小的情况下,可以利用杆长差对刚度及摩擦力的优化特性,实现宽频段隔振优化。

