基于FEA的手柄拉簧失效分析与流程优化设计
邹春龙,邓威,王生怀,邓小雯
(1.湖北汽车工业学院,湖北十堰 442002;2.湖北中航精机科技有限公司,湖北襄阳 441005)
基于FEA的手柄拉簧失效分析与流程优化设计
邹春龙1,邓威2,王生怀1,邓小雯1
(1.湖北汽车工业学院,湖北十堰 442002;2.湖北中航精机科技有限公司,湖北襄阳 441005)
拉簧是汽车座椅调角器中的重要零件。按传统查表法和公式法设计拉簧,疲劳次数增加至2万次左右,常出现疲劳失效,造成反复更改设计和浪费。通过疲劳实验分析失效形式主要为弯钩疲劳断裂,且采用理论计算和FEA(有限元)分析钩环处的应力集中最大。研究了簧丝直径d、中径D、圈数n等参数对拉簧寿命影响,得到最大应力与抗拉极限的比值是衡量疲劳寿命的参数,比值越小,零件疲劳寿命越大。提出流程优化设计,给出设计和校核过程中安全系数S和弯钩处应力值校核的范围,优先校核簧体和钩环应力,减少拉簧设计的不确定因素,极大地提高设计成功率。
拉簧;疲劳失效;FEA;应力分析;优化设计
0 引言
手柄拉簧在手动调节座椅中已广泛采用,但很多座椅厂家反馈拉簧在做2万次以上寿命试验时,经常出现疲劳断裂的问题,需要重复多次对其进行设计改进,影响座椅项目的转批生产。拉簧疲劳失效成为调角器寿命试验通过的制约因素,而影响其疲劳失效的因素很多。目前,设计拉簧时多采用查表法和计算法,对手柄拉簧失效原理的系统性分析很少,设计成功率较低,造成很大的成本浪费。
对拉簧失效原理和设计流程进行系统化研究意义深远。以某拉簧为例,先用查表法和公式法进行设计,通过疲劳实验和有限元法分析拉簧失效和受力后应力分布的关系,分析设计不足,研究强度校核与寿命关系,提出流程优化设计思路,减少拉簧设计的不确定因素,提高设计成功率。
1 拉簧的原始设计输入
某座椅事业部要求:新研发手动正驾调角器采用双只全齿核心件,俗称双边调角器,调角器两边都有板簧,手柄总长达164 mm(手柄末端距旋转中心),总质量达0.091 kg。靠背由联杆连接保证解锁同步性。由于这种结构的调角器板簧提供的回复力较大,需在手柄上增加拉簧以保证手柄落锁的可靠性。调角器安装空间要求拉簧中径D≈9.7 mm,外径D2<13 mm,初拉力23 N,最大拉力为76~79 N,拉簧在调角器解锁过程中不与其他构件发生干涉,拉簧的伸长量约为33.6 mm。
2 拉簧的拉力及外形设计
根据工作极限载荷选取材料直径d及弹簧中径D,查机械手册弹簧表[1],工作极限载荷:
Pm≥1.25Pn=1.25×79=98.75 N
(1)
材料直径取d≈1.3 mm,弹簧中径D≈11,按照拉簧以往设计经验,对表中的钢丝直径为1.2与1.4 mm、中径为11 mm的数据进行插值处理。

图1 公式法拉簧设计步骤
圆柱螺旋弹簧分类:Ⅰ类——受循环载荷作用次数在1×106次以上的弹簧;Ⅱ类——受循环载荷作用次数在1×103~1×106次范围内及受冲击载荷的弹簧;Ⅲ类—受静载荷及受循环载荷作用次数在1×103以下的弹簧。
2.1 根据工作条件选取材料及其许用应力
因为手柄拉簧的工作循环次数为20 000次,应按第Ⅱ类弹簧进行考虑。现选用弹簧钢丝65 Mn。并根据中径D≈9.7 mm、外径D2<13 mm,估取弹簧钢丝直径d<3.3 mm。 查资料可知65Mn钢丝的许用切应力τP=325 MPa。
2.2 根据强度条件计算钢丝直径
如图1所示公式法,拉簧最大应力产生在弹簧丝截面内侧的m点[2](簧丝截面直径内侧端点)。弹簧的破坏也是多由这点开始。Ⅱ类受循环载荷作用次数在1×103~1×106,跨度过大,τP=325 MPa是满足10万次的极限要求。若直接采用此值会造成簧丝直径过大,造成成本剧增。而客户要求2.4万次,更接近Ⅲ类(τP=380 MPa),取中间值370 MPa。65Mn簧丝经过喷丸处理,其许用应力可提高20%。后期工艺进行强压处理,许用应力可进一步提高10%~20%。即τP=370×1.4=518 MPa。
弹簧簧丝内侧最大应力及强度条件:

(2)


(3)
拉簧的簧丝直径d和拉簧的中径D优先标准值,取d=1.5 mm或1.6 mm,在此钢丝直径范围内拉簧σBP、τP不变,查表取D=12 mm,C=D/d=12/1.5=8。所得尺寸符合设计要求的限制条件。
2.3 根据刚度条件计算圈数n
弹簧的刚度为:

(4)

(5)
取n2=14圈,此时弹簧的刚度为:

(6)
2.4 验算
弹簧的初拉力:
F0=F1-Kfλ1=23-7×2.144=7.992 N
(7)
初应力τ0按照下式得:

(8)
其中K按下式计算:

(9)
当C=8时,初应力的推荐值为43~120 MPa,故此初应力合适。
极限工作应力:
τlim=0.56σB=0.56×1 800=1 008 MPa
(10)
极限工作载荷:

(11)
极限工作载荷大于最大工作载荷。
2.5 校核
对于受循环载荷的重要载荷(Ⅰ,Ⅱ类)应进行疲劳强度验算;受循环载荷次数少或所受循环载荷变化幅度较小时,应进行静强度验算。当两者不易区分时,要同时进行两种强度验算。
(1)疲劳强度验算(只与钢丝直径相关)
最大工作载荷所产生的最大切应力:

(12)
最小工作载荷所产生的最大切应力:

(13)
弹簧在脉动循环载荷下的剪切疲劳强度,对于高优质刚、不锈钢丝和硅青铜一般选取[3]:
τ0=0.5(0.35σb+0.45σb)=810 MPa
(14)
按1万次计算安全系数:
S=(τ0+0.75τmin)/τmax=1.175
(15)
按10万次计算安全系数:
S=0.96
(16)
许用安全系数,当弹簧的设计计算和材料试验精确度高时,取Sp=1.3~1.7。
(2)静强度验算
安全系数:

(17)
按查表法所得拉簧直径可选1.3、1.4、1.5 mm和公式法设计的拉簧直径可选1.5、1.6 mm,如后文所示。
3 基于FEA的手柄拉簧失效形式及应力分析
3.1 拉簧的疲劳试验
拉簧的失效是一种渐进的失效现象,其过程包括裂纹萌生、扩展直至断裂。弹簧的失效包含疲劳断裂和应力松弛。为验证拉簧实际工况下失效形式及寿命,拉簧需要挂在调角器上随手柄全行程进行“解锁→释放”操作,如图2所示,通过调整气缸,将疲劳试验的频次控制为1次/5 s,计数器满24 000次后,回路自动切断。试验记录结果如表1所示。

图2 拉簧疲劳试验

钢丝直径/mm工作载荷平均疲劳次数失效形式ϕ1.2 65Mn79(0.9~1.5)×104钩环处断裂ϕ1.2 琴钢丝79(1.3~1.9)×104钩环处断裂ϕ1.3 65Mn79(1.0~1.7)×104钩环处断裂ϕ1.3 琴钢丝79(1.6~2.1)×104钩环处断裂ϕ1.4 65Mn73(1.6~1.9)×104钩环处断裂ϕ1.4 琴钢丝73(2.0~2.6)×104钩环处断裂ϕ1.5 65Mn79(2.4~3)×104钩环处断裂ϕ1.5 琴钢丝79(2.4~3)×104钩环处断裂ϕ1.5 65Mn73(2.3~2.8)×104钩环处断裂ϕ1.5 琴钢丝73(2.4~3.5)×104OK
手柄拉簧失效形式主要是钩环处疲劳断裂。采用公式法和查表法设计时,常比较重视拉簧的材料选用、拉簧簧体的应力和加工工艺,而忽略了拉簧钩环处的r对应力集中的关系[4],造成拉簧断裂失效的情况时常发生,影响了产品的质量。拉簧钩环急弯处的r也需要经过强度校核后再确定其数值,以提高手柄拉簧质量和可靠性。
3.2 拉簧弯钩的应力分析
拉伸弹簧在拉伸时,钩环在点A、B处受力如图3所示,承受最大弯曲应力和切应力。对重要的拉伸弹簧,其应力可按下式分别计算:

(18)

(19)
当直径为1.3 mm时:
点A处应力:σmax=1 913.42 MPa
点B处应力:τmax=1 371.28 MPa
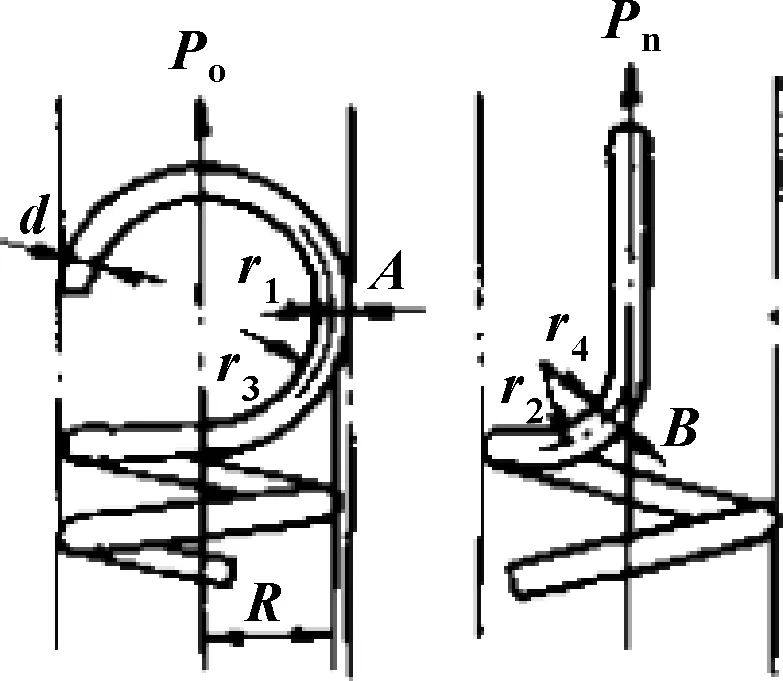
图3 拉簧弯钩处受力图
点A、B处的应力均超出了材料的许用应力(以65Mn为材料进行校验,极限抗拉σB=1 800 MPa) ,而且超出了极限抗拉应力和极限剪切应力。
σmax=1 913.42 MPa>σBP=710 MPa
τmax=1 371.28 MPa>τP=380 MPa
当直径为1.5 mm时:
点A处应力:σmax=1 430 MPa
点B处应力:τmax=715 MPa
点A、B处的应力均超出了材料的许用应力(以65Mn为材料进行校验),但是未超出极限抗拉应力和极限剪切应力。
σmax=1 430 MPa>σBP=710 MPa
τmax=715 MPa>τP=380 MPa
故弯钩处承受拉簧的主要变形和拉力[5]。拉簧钩环急弯处r参数直接影响到拉簧使用的稳定性和可靠性。
3.3 拉簧应力分布研究
为了进一步研究不同规格拉簧在受载荷情况下各结构的受力情况,用有限元软件对其受力后的应力分布进行分析。边界条件:拉簧一端固定约束,一端施加79 N截荷。
拉簧受力后, 如图4所示,应力集中主要分布在弯曲程度较大的部位,如内圈和弯勾处,且弯勾处应力最大。拉簧直径分别为1.3和1.5 mm ,FEA分析弯勾处应力分别为1 818.4和1 503.0 MPa,其中直径1.3 mm处弯勾材料已屈服,而簧身应力只有1 362~1 509 MPa。由应力分布分析结果和试验测定拉簧失效模式可得,拉簧簧身的寿命和弯钩的寿命是两个截然不同的概念。拉簧簧身的疲劳寿命远大于其钩环的疲劳寿命。在第Ⅱ类寿命次数10万次以内,拉簧簧体的寿命受簧丝的直径影响较小,但弯钩的寿命受直径影响较大,如图4和表1所示,随着簧丝直径的增加,钩环的寿命次数呈增加趋势。且同直径规格的拉簧,选择强度等级较高的材料(琴钢丝)寿命可增加3 000~5 000次。
3.4 不同规格拉簧的应力比较
不同规格拉簧的应力比较分别如图5—8所示。拉簧1(φ1.3,D9.7)位移与应力如图5所示;拉簧2(φ1.4,D9.7)位移与应力如图6所示;拉簧3(φ1.5,D9.7)位移与应力如图7所示;拉簧4(φ1.5,D12)位移与应力如图8所示。
(1)对比拉簧1、拉簧2和拉簧3,拉簧3刚度最大,应力最小,且疲劳寿命最大;
(2)对比拉簧3和拉簧4,载荷为72 N时,拉簧3刚度增加了82.4%,应力减少了20.2%;载荷为79 N时,拉簧3刚度增加了82.5%,应力减少了20.2%。

图5 拉簧1(φ1.3 mm,D9.7 mm)位移与应力
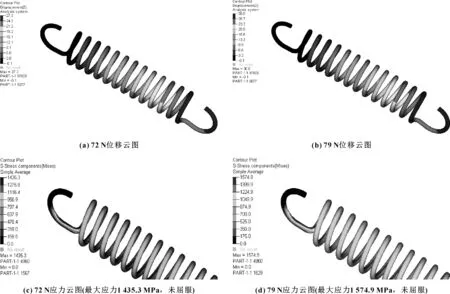
图6 拉簧2(φ1.4,D9.7)位移与应力
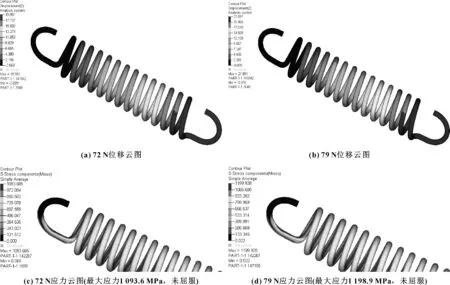
图7 拉簧3(φ1.5,D9.7)位移与应力

图8 拉簧4(φ1.5,D12)位移与应力
如表2所示:最大应力与抗拉极限的比值是衡量疲劳寿命的参数,该比值越小,零件疲劳寿命越大。

表2 拉簧疲劳试验结果
4 拉簧的流程优化设计
4.1 流程优化的可行性分析
在拉簧传统设计中,簧体寿命和钩环的强度校核一般在拉簧设计完成后进行[6]。如此设计的拉簧寿命和钩环强度常不符合要求,导致设计的反复重来。故拉簧设计输入时,先定义拉簧的最大和最小载荷,簧体和钩环在A、B处承受的最大弯曲应力和切应力也可换算成与簧丝直径相关的表达式。这样就可以在设计拉簧之初,对所选拉簧的规格进行评估,判定是否满足寿命和弯钩强度要求,减少设计不合格概率。
拉簧校核中经常出现簧体安全系数满足不了1.3~2.2(满足100万次标准)的要求,从以往的经验看,手柄拉簧目前的寿命只需要在3万次,远远小于100万次的标准,且在疲劳试验中未出现簧体断裂,安全系数S可放宽至S>0.9。
4.2 流程优化设计
拉簧流程化设计如图9所示。

图9 拉簧的流程化设计
首先根据调角器拉簧挂接布置的空间,初步估计一个合适的拉簧直径。查找该直径对应下的拉簧拉伸极限强度σB,根据设计寿命要求所属三类簧的设计条件,选取拉簧许用切应力τP(拉簧极限切应力远大于此值)。根据拉簧簧丝内侧的最大应力和强度条件,估算拉簧的直径d。再同时校核簧体和弯钩强度,即安全系数S和钩环点A拉应力、点B切应力。校核弯钩处点A拉应力、点B切应力时,通常也会遇到点A的最大拉伸应力和点B的最大切应力大于许用值σBP或者τP,若小于材料的最大拉伸应力和最大剪切应力,可以保守地进行后续地设计和试验。否则,重选钢丝直径或材料。
若通过或者接近保守值,再进行后续刚度和圈数设计,圈数取整后,进一步计算拉簧的初拉力和极限工作载荷。此时完成拉簧的理论设计,供应商送样进行指定次数N的疲劳寿命试验。记录试验次数N1,试验通过则锁定拉簧状态,或者试验接近N(N-N1<3 000次),则可以选择强度等于高一级的材料进行“提高”替代,如65Mn改由琴钢丝替代。若试验次数N1与指定目标N相差太大,需重选择钢丝直径和材料。
设计的拉簧图纸如图10所示。

图10 拉簧图纸
5 总结
手柄拉簧失效形式主要是钩环处疲劳断裂。通过实验和有限元法分析拉簧受力应力集中主要分布在弯曲程度较大的部位,如内圈和弯勾处,且弯勾处应力最大,拉簧簧身的疲劳寿命远大于其钩环的疲劳寿命。故拉簧设计成功的关键在于弯勾处的设计,应优先校核簧体和钩环应力,优化设计流程以减少设计不合格概率。在设计时,在校核关键参数如弯钩处的点A拉应力、点B切应力时,若点A的最大拉伸应力和点B的最大切应力大于许用值σBP或者τP,而小于材料的最大拉伸应力和剪切应力,可进行后续的设计和试验。最大应力与抗拉极限的比值是衡量疲劳寿命的参数,该比值越小,零件疲劳寿命越大。
[1]成大先.机械设计手册[M].6版.北京:化学工业出版社,2016.
[2]韩泽光.圆柱形扭转螺旋弹簧的可靠性优化设计[J].机械研究与应用,2000,13(4):25-26.
HAN Z G.Reliability Optimal Design of Helical Torsion Spring[J].Mechanical Research & Application,2000,13(4):25-26.
[3]张英会,刘辉航,王德成.弹簧手册[M].2版.北京:机械工业出版社,2008.
[4]张大利.砼回弹仪弹击拉簧失效分析[J].中国计量,2006(7):65-66.
[5]菅军伟,邢献强.拉簧拉钩折弯处断裂机制研究[J].金属制品,2015,41(2):37-40.
JIAN J W,XING X Q.Research of Tension Spring Hook Bending Fracture Mechanism[J].Steel Wire Products,2015,41(2):37-40.
[6]王梅,陈国定,肖勇.基于多失效模式的扭簧可靠性优化分析[J].中国空间科学技术,2011,31(5):57-63.
WANG M,CHEN G D,XIAO Y.Optimal Analysis of the Reliability for Torsion Spring Based on Multi-failure Modes[J].Chinese Space Science and Technology,2011,31(5):57-63.
FailureAnalysisandOptimizationDesignforHandleTensionSpring
ZOU Chunlong1,DENG Wei2,WANG Shenghuai1,DENG Xiaowen1
(1.Hubei University of Automotive Technology,Shiyan Hubei 442002,China;2.AVIC Hubei Aviation Precision Machinery Technology Co.,Ltd.,Xiangyang Hubei 441005,China)
Tension spring is an important part of automotive seat recliner. The tension spring designed with traditional look-up table method and formula method, often appears fatigue failure when fatigue number increases to about 20 000 times, causing repeated design change and waste. Through fatigue experiment analysis, the main failure mode of tension spring was the hook fatigue fracture, and the stress concentration in shackle was the largest by theory and FEA analysis. The influences of the diameterd, the pitch diameterD, the number of turnsnof the spring were studied. It is shown that the ratio of maximum stress and tensile limit was the parameter to measure fatigue life. The smaller the ratio is, the greater the fatigue life of parts is. The optimization design process was put forward, the safety factorSand the checking range of hook stress value were given during the design and checking process. The spring body and the shackle stress were checked first, reducing the uncertainty of tension spring design, greatly increasing the success rate of design.
Tension spring; Fatigue failure; FEA; Stress analysis; Optimization design
2017-04-07
湖北省教育厅科学技术研究重点项目(D20141802)
邹春龙(1988—),男,硕士,工程师,主要研究方向为机械产品优化设计、汽车座椅精密调节机构设计。E-mail:zouchunlongh_hapm@163.com。
10.19466/j.cnki.1674-1986.2017.08.007
TH703.8
A
1674-1986(2017)08-031-07

