基于PDMS薄膜的等离子体光栅仿真分析

陈壮壮，王志斌，李克武，吴笑男

（中北大学 理学院 山西省光电信息与仪器工程技术研究中心，山西 太原 030051）

引言

光栅（grating）属于应用广泛的光学元件，在光学传感、集成光路、光信息处理、光通信等光学应用领域都呈现了举足轻重的作用。目前，该元件主要运用在纳米级别。国内外对于新型的光学元件纳米级光栅在生物传感、光子晶体[1-3]等多领域都有深入的研究和探讨。

在柔性器件领域，柔性电子设备主要有两类，其中有机半导体[4-6]占比最高。而在制备其他的柔性元件时，则主要依托聚二甲基硅氧烷（polydimethylsiloxane，PDMS）[7]等一些具有良好可拉伸性能的材料，以及其他具有延展性的结构类体系材料。PDMS 薄膜不仅拉伸性能良好，且具有亲肤性和无毒性。因此，PDMS薄膜作为柔性材料的代表受到了大家的青睐，被广泛应用在柔性电子设备和可穿戴设备[8]之中。在这些应用中，作为柔性支撑材料是PDMS 薄膜本身最常见的作用。

本文选用时域有限差分（finite difference time domain，FDTD）法，通过相关仿真软件FDTD Solutions，建立一种以PDMS 薄膜为基板的具有周期边界条件的二维金属等离子体光栅仿真结构。通过对光栅施加应力，改变PDMS 薄膜等离子体光栅的参数（即周期、占空比及Au 膜厚度），并对其进行设计仿真和理论计算。通过对其共振波长特性的探究，本文提出了对应力最为敏感的等离子体光栅结构。最后将仿真结果与理论数值做对比，并计算出相对误差的大小。

1 基本原理

1.1 等离子体光栅理论模型

等离子体作为一种比较特殊的物质状态，是由高密度且呈均等分布状态的两种带电自由粒子所构成的[9]，它本身不会产生空间电荷，对外也不显电性。基于光栅耦合的原理，能够引起表面等离子体波，其示意图如图1 所示。当光波（包括极化光p）进入光栅表面的电介质时，光栅本身的周期结构会导致一系列衍射。衍射光线被反射的同时，按照不同的衍射角进行衍射，继而出现不同的衍射级次。当某一级次的波向量与表面等离子体波的波向量在界面方向上的投射相一致时，表面等离子体波便可以在光栅表面激发[9]。

图1 光栅耦合模型Fig.1 Grating coupling model

对于入射角为θ的光，在基板和空气中传播的衍射级数与基板表面平行的衍射波的波长λ为

式中：n1为PDMS 基底的折射率；n2为空气的折射率；m为任意整数，对应不同衍射级次，m＞0 时（1）式、（2）式取正，m＜0 时取负；p为光栅周期。（1）式和（2）式分别为等离子体光栅反射和透射时衍射级数与波长的关系。

1.2 表面等离子体共振原理

众所周知，自由电子存在于金属内部的同时，也大量存在于其表面，且组成独立的自由电子团，也就是等离子体（plasmon）；另一方面，将存在于金属表面高活性的自由电子团定义为表面等离子体。当入射光照射到金属表面时，会与它产生的自由电子团振动频率相同从而引起共振，便产生了表面等离子体共振[10]（surface plasmon resonance，SPR）。与SPR 一样，光和电子的相互作用也可以产生局域表面等离子体共振（localized surface plasmon resonance，LSPR）。当光束照射到金属表面时，金属表面的自由电子迅速激发，并与入射光中的光子以一致的频率在晶格中共振[11]，在光谱上显示出紫外可见光范围内的强共振吸收或散射峰。而对于金纳米材料，LSPR 特性明显改变的直观表现是峰值和颜色的变化，因而可以在传感器[12]等众多领域中发挥关键的作用。

表面晶格共振是由金属颗粒的局域表面等离激元与瑞利反常[13]（rayleighabnormal，RAs）产生衍射耦合引起的。瑞利反常，这是由平行于基板表面的衍射阶数叠加和来自单个纳米线的局域表面等离子体共振（LSPR）引起的。瑞利反常产生时，某些衍射级次对应的衍射角恰好为90°，意味着它们处于倏逝波[8]或传播波（不附带能量或附带有能量）的临界状态。

由光栅方程可知，假设光栅常数[8]为a，空气中的入射光照射到光栅上的角度为θ，ε1代表金薄膜的介电常数，ε2代表空气介电常数，沿光栅表面产生SPPs[8]的条件可以写成：

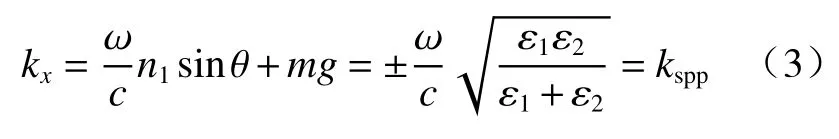
式中：g为光栅波矢，且g=2π/a，ω=2π/λ；m表示衍射级次。

当光栅常数和入射角合适时，金属表面可产生SPPs 波。这种激发表面等离子体共振的方式适用于金属/电介质界面和空气/金属界面[14]。通过计算（2）式和（3）式，可以得出等离子体光栅透射时所产生的共振波长λspp为

式中：p和n1分别表示光栅的周期和基底的折射率。

1.3 PDMS 等离子体光栅应力应变原理

由胡克弹性定律[15-16]可知，物体在弹性区间内所受的外力与它单向拉伸的变量成线性关系，即应力σ和应变ε成正比：

式中：E 为弹性模量或杨氏模量[16]。

在本文中，我们采用FDTD Solutions 模拟分析了PDMS 基板上的等离子体晶格光栅的视向光学响应。光栅所用的材料为金，一般而言，金、银等金属材料都可以用来制作光栅，但是银在制作过程中容易发生氧化，在其表面形成一种氧化膜，从而会对实验结果产生影响。因此，从光学特性来看我们选择了金作为PDMS 光栅的材料。

对等离子体光栅沿栅线方向施加压力，改变等离子体光栅参数，当压力变大时，光栅的周期、占空比都会不断减小，金膜厚度则随着压力的增大而逐渐增大。本文中将通过仿真等离子体光栅的透射率来观察光栅参数变化时对光栅共振吸收峰的影响，并得出光栅参数对光栅应力的响应敏感程度；其次将仿真所得结果与理论计算值作比较得出相对误差的大小。

2 等离子体光栅仿真模型结构设计

FDTD Solutions 是一款对微结构进行仿真设计分析的高性能软件。该软件能经过脚本语言构建任何形状的二维和三维结构，借助软件提供的综合数据分析和作图，可以很快地解决问题。此外，FDTD Solutions[17]可以根据本文设计模型结构进行选取，可以用来建立仿真周期性光栅结构，并对简化的二维模型进行设计分析。用FDTD 仿真光栅，需要建立物理模型、定义仿真区域、设置光源和监视器，最后进行运行及分析。

我们用FDTD 建立了具有边界周期条件的yz平面等离子体晶格光栅的视向光学响应的二维模型。如图2 所示，已知PDMS 基底的折射率n1为1.55，空气介质中的折射率n2设置为1，光栅的材料是Au，用p表示光栅周期，用h表示刻槽深度，其中金膜的厚度为b，PDMS 宽度为w，平面波斜入射时的角度为θ，光栅的占空比f=w/p。

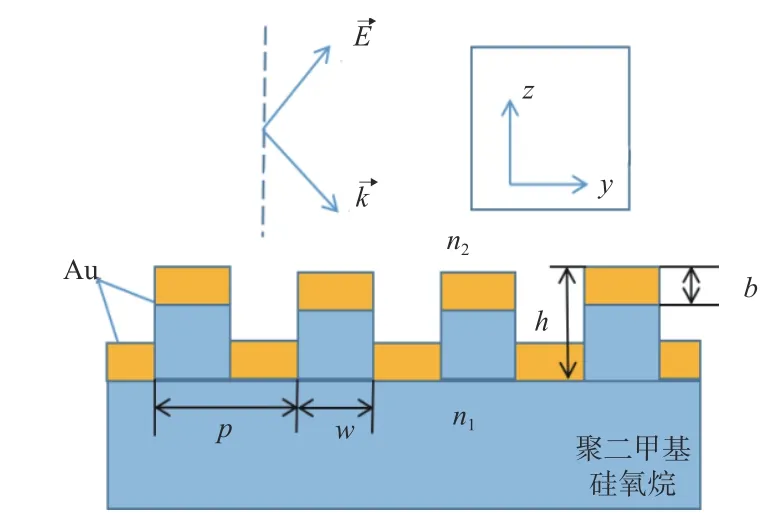
图2 光栅结构示意图Fig.2 Schematic diagram of grating structure

光栅上的光沿y方向线性极化，考虑到模拟的光栅在结构上属于周期性，因此在仿真中竖直方向结构为无限周期边界条件，选择完全边界条件[18-20]将照射的电磁波全部吸收无反射，水平方向结构则采用周期边界条件。设置周期性边界条件后，建立仿真区域时只需对其中一个周期进行建模，便可实现对整个周期排列的结构进行电磁场仿真分析[21]，极大地提高了工作效率。

3 仿真结果与理论对比

3.1 周期改变对等离子体光栅共振峰的影响

光从空气向PDMS 薄膜光栅入射时，此时光入射的角度θ为50°。考虑光的入射波长范围为0.4 μm～1.5 μm，PDMS 宽 度w为0.25 μm，光 栅 槽 深h为0.12 μm，其中金膜厚度b为0.02 μm，占空比f为50%。本仿真中光栅周期p的取值范围为0.4 μm～0.7 μm，步长为0.05 μm，用FDTD Solutions 进行仿真得到的透过率结果如图3 所示。

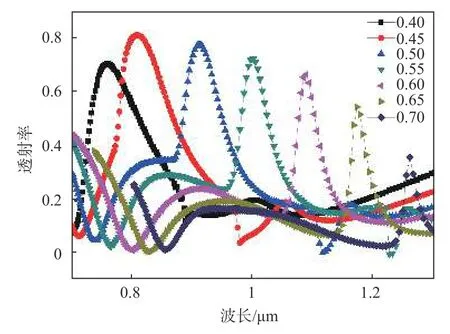
图3 不同周期的共振谱Fig.3 Resonance spectrum of different periods

由图3 可知，在波长相同的入射光条件下，不同周期激发产生表面等离子体共振峰的位置不同。其次，当周期从0.4 μm～0.45 μm 变化时，光栅的共振峰光谱发生了红移，共振深度逐渐增加，共振半峰宽度逐渐减小；但当周期在0.45 μm～0.7 μm区间内时，共振峰光谱又发生红移，共振深度逐渐缩小，共振半峰宽度随之递减，但其激发的等离子体光栅共振吸收峰的波长随着周期变大而逐渐增大，且周期每增大0.05 μm，对应的共振峰波长增加0.1 μm。图3 可以看出周期在0.65 μm～0.7 μm时，透射率变化最明显，在0.7 μm 时共振峰最尖锐，共振半峰宽度最窄，因此对应力响应最敏感的周期为0.7 μm。

图4 表明了共振波长与周期的变化关系，通过（2）式计算可得周期为0.4 μm，0.45 μm，0.5 μm，0.55 μm，0.6 μm，0.65 μm，0.7 μm 时的共振波长分别为0.704 μm，0.792 μm，0.88 μm，0.918 μm，1.056 μm，1.144 μm，1.232 μm，可知理论数值与仿真所得结果都吻合，其中周期为0.7 μm 时共振波长为1.251 μm，相对误差为1.5%。

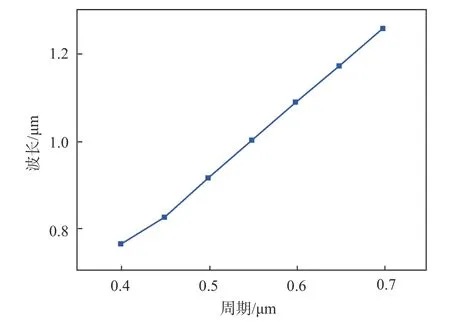
图4 共振波长与周期的变化关系Fig.4 Change relationship between resonance wavelength and period

3.2 金膜厚度改变对等离子体光栅共振峰的影响

不同金膜厚度会影响金属性能，当金膜厚度较薄时，其表面电子浓度低，会导致SPR 响应不明显。只有金膜厚度一定、形成均匀平滑的薄膜层时，产生SPR 现象才更为稳定。如果金膜厚度再逐渐增加，那么光谱曲线中的谐振共振峰耦合深度会变浅。

本文中设置其余条件不变，取p=0.7 μm，f=50%，将金膜厚度b的取值范围设置为0.01 μm～0.07 μm，步长为0.01 μm，用FDTD Solutions 仿真得到的透过率结果如图5 所示。

图5 不同金膜厚度的共振谱Fig.5 Resonance spectrum with different gold film thicknesses

其中图5 中的嵌图为光栅金膜厚度改变时共振波长的局部放大图。光栅周期为0.7 μm 时，由嵌图可知，金膜厚度小于0.02 μm 时，共振深度增大，等离子体光栅共振波长随之增大；金膜厚度大于0.02 μm 时，个别数据除外，共振深度逐渐增大，共振波长大小基本不变，且金膜厚度从0.01 μm～0.02 μm 变化时，共振吸收峰的深度增大得最为明显。同时金膜厚度为0.02 μm 时，光栅的共振深度最深，共振半峰宽度最窄。因此可得金膜厚度为0.02 μm 时，对应力的响应最为敏感。

图6 表明了共振波长和金膜厚度的变化关系，可知光栅周期为0.7 μm 时，FDTD 仿真所得的共振波长为1.25 μm，与理论值对比后，其相对误差是1.4%。

3.3 占空比改变对等离子体光栅共振峰的影响

其余参数保持不变，光栅周期p设置为0.7 μm，金膜厚度b为0.02 μm，占空比f的取值范围为35%～65%，步长为5%，用FDTD Solutions 仿真得到的透过率结果如图7 所示。

图6 共振波长和金膜厚度的变化关系Fig.6 Change relationship between resonance wavelength and gold film thickness

图7 不同占空比的共振谱Fig.7 Resonance spectrum with different duty cycle

其中图7 中的嵌图为光栅占空比改变时共振波长的局部放大图。光栅周期为0.7 μm 时，由嵌图可知，光栅占空比的变化并不会引起共振波长的改变。当占空比小于55%、f增加时，共振深度变深；当占空比大于55%时，共振深度变浅；当占空比等于55%时，共振半峰宽度最窄。因此在SPR测量中，占空比为55%时对应力的响应最为敏感。

图8 表明了共振波长和占空比的变化关系，可知光栅周期为0.7 μm 时，FDTD 仿真所得的共振波长为1.254 μm，与理论值对比后，其相对误差是1.7%。

图8 共振波长和占空比的变化关系Fig.8 Change relationship between resonance wavelength and duty cycle

4 结论

本文利用PDMS 薄膜优越的拉伸特性，提出了一种以PDMS 薄膜为基底的具有周期性边界条件的金属等离子体光栅结构。借助FDTD Solutions光学仿真软件，通过对等离子体光栅施加应力，得出了光栅周期、占空比及金膜厚度改变时对等离子体光栅共振峰波长的影响以及对力的响应敏感程度。结果表明，当金膜厚度b和占空比f一定时，周期p为0.7 μm 的等离子体光栅的共振半峰宽度最窄，共振峰最尖锐；当占空比f和周期p一定时，金膜厚度b为0.02 μm 的光栅的共振深度最深，共振半峰宽度最窄；当金膜厚度b和周期p一定时，占空比f为55%的光栅的共振深度最深，共振半峰宽度最窄。

综上所述，当光栅周期p=0.7 μm，占空比f=55%，金膜厚度b=0.02 μm 时，对光栅施加应力所产生的响应最为敏感；其次，将仿真所得的不同周期时的共振峰波长与理论计算值相比较可知，二者结果相吻合。并且当周期为0.7 μm 时，共振吸收峰的波长为1.251 μm，理论与仿真所得结果的相对误差都小于2%。该方法可以为传感器、光谱仪等光学应用领域提供参考。