光束斜入射的折反射组合光学系统的像差计算
赵小楠,吕丽军
(上海大学 精密仪器及机械系,上海 200072)
引言
近年来,随着机器人、计算机视觉、虚拟现实及航天等应用领域的日益发展,单一折射或反射镜光学系统出现了一定的局限性,难以满足科研乃至日常生产应用需求。折反射组合光学系统具有扩大视场范围,结构简单紧凑等优点,常应用在折反射全景成像系统[1-4]以及二次旋转圆锥曲面面形检测[5-6]中。因此,折反射组合光学系统的成像分析成为一个重要的研究课题。
光学系统成像质量的分析评价大多是围绕近轴光学系统展开的,评价工作的主要依据是赛德尔像差理论[7],赛德尔像差理论对入射角小于 30°的近轴光学系统进行像差分析时计算精度较高。但是,对于光束斜入射的折反射组合光学系统,光束以较大的入射角(这里一般指入射角远大于 30°)打在光学元件表面,经过光学系统后,在子午和弧矢平面内光束聚焦位置及波阵面形状完全不一致,此时该类系统具备平面对称光学系统的特点,赛德尔像差理论则不再适用。
吕丽军教授等人基于波像差的方法,针对平面对称光学系统在子午和弧矢平面内焦点完全不一致的特点,提出以超环面作为参考波阵面,发展了平面对称光栅系统的像差理论[8]。该理论适用于斜入射甚至掠入射(入射角达到 80°,甚至 89°以上)的光栅或反射镜光学系统的像差分析。此外,它还可以研究任意二次旋转圆锥曲面,如椭球面、超环面和抛物面等。
下面第1 节中主要在平面对称光栅系统波像差理论的基础上,推导出光束斜入射的折射光学系统的波像差计算表达式[9]。在第2 节中,给出多元件光学系统的波像差以及系统的光线像差的计算表达式。最后一节中,将潘君骅院士与作者在椭球镜面形误差检测中的检测方法进行实验模拟,利用扩展后的平面对称光学系统的像差表达式对椭球镜面形误差检测光学系统进行成像计算,并与Zemax 软件光线追迹结果进行比较,验证将该像差理论应用于光束斜入射的折反射组合光学系统成像分析的正确性。
在合肥同步辐射光源一期工程中,潘君骅院士与吕丽军教授对光束线装置中的椭球面反射镜进行面形误差检测,应用平面对称光学系统的像差理论,对实际椭球镜的光学参数进行计算,通过比较实际成像光斑与理论计算结果,判断椭球镜面形误差是否满足设计标准。本文在第3 节中将它作为一个实例,应用平面对称光学系统像差理论来计算光束斜入射的折反射组合光学系统的像差,以验证我们理论工作的有效性。
1 光束斜入射的折射光学系统波像差
1.1 平面对称光学系统的波像差系数

图1 平面对称反射/折射光学系统成像示意图Fig.1 Imaging schematic of plane-symmetric catadioptric optical system
图1 为平面对称光学系统的反射/折射成像示意图,图1(a)和图1(b)分别表示反射和折射光学系统。
光学系统是关于χOz′平面对称,O为光学元件表面的顶点,O0OO1位于对称平面χOz′内,是光学系统的基准光线。由光源S0发 出的光线定义为主光线;xyz表示孔径光阑坐标系,原点为;z′=f(χ,η)为光学元件在光学元件表面坐标系 χ ηz′下的面形方程;n0和n1分别表示物方和像方空间的折射率;u、u′分别表示物方和像方的视场角; α 和 β分别表示基准光线O0OO1在各个光学元件表面的入射角和反射角/折射角,它们是参照z′轴的正方向来定义的,当z′轴逆时针方向旋转到该光线时角度的符号规定为正,反之为负。
在平面对称光栅系统波像差理论中,采用超环面作为参考波阵面来定义波像差,并应用光线几何方程和多项式拟合法求出光线在光学元件表面和入射波阵面之间的位置坐标映射关系,导出平面对称光栅系统的波像差表达式。
应用波像差的方法求解平面对称光学系统的波像差时,需要定义平面对称光学元件的面形。平面对称光学元件的面形方程一般用下式表示[10-11]:

对于平面对称光学系统的四阶波像差,面形方程式(1)需要关于x、y进行泰勒级数展开至四阶,具体表达式为
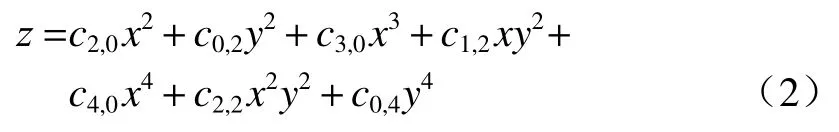
式中:ci,j为光学元件面形系数,当光学面为二次旋转圆锥曲面时,其面形系数由文献[12]的公式(24)给出。
推导出的平面对称光栅系统的波像差,由物方光束和像方光束两部分贡献,因此波像差可以表示为

将Wobj和Wima展开为关于x、y、u的四阶泰勒级数,可得到:

式中:Mi jk=Mijk(α,rm,rs,l)表示物方空间的波像差系数,由文献[8]中的附录A 给出。像方空间的波像差系数只要对物方空间相关参量进行替换,就可以得到分别表示光学元件在物方和像方空间内的子午焦距和弧矢焦距,l和l′分别表示物方和像方空间内的光瞳位置参量[13]。
折射情况和反射情况下的光学系统具有相似的光线几何特征,只是像方空间的折射率以及入射角的规定不同。在光束斜入射的折射情况下的平面对称光学系统中,入射光线关于z′轴正方向的方向角应该为α+180°,如图1(b)所示。所以在这种情况下的波像差计算中,只需要在文献[8]推导出的反射光学系统的波像差计算表达式的基础上,将其中的参量 α用α+180°来替换,并且需要考虑光学元件,物方空间的折射率n0和像方空间的折射率n1。因此,对于反射和折射光学面,波像差计算的统一表达式为

当n0=n1=1时,上式表示为反射光学面的波像差,否则代表折射光学面。
将u′=−(n0/n1)≡n0/1u代入(6)式,可得到波像差W的四阶泰勒级数形式:

式中Wijk为波像差系数。它的具体表达式为
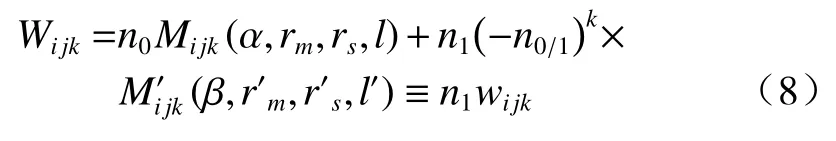
其中,
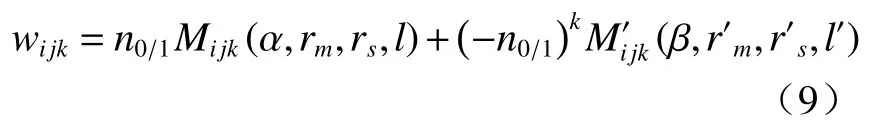
1.2 光学系统的四阶波像差理论
在波像差的求解过程中,需要知道光学系统的基本参数。对于轴对称光学系统,一般基于高斯光学定义光学系统参数。类似地,对于平面对称光学系统,准基像差理论应用一二阶波像差系数定义光学系统像差的参考“基准”。首先,通过W100=0来定义光学系统的基准光线,得到反射或折射光学面的Snell 定律:

其次,通过应用W200=0和W020=0来分别确定光学元件在子午和弧矢平面内的焦平面位置:

另外,应用W011=0来确定主光线的位置(也就是孔径光阑位置):

根据(12)式和(13)式可以得到物方空间与像方空间内的孔径光阑位置之间的关系为

因此,对于准基像差理论,即在满足(10)式~(13)式的条件下,决定光学系统的四阶单色波像差项为

2 折反射组合光学系统的像差
2.1 光线像差
文献[8]介绍了在平面对称光栅系统中如何利用波像差系数求解像平面上的光线像差。对于折射光学系统来说,求解方法相同,但是在求解子午和弧矢方向上实际光线与参考出射波阵面的法线之间的角度偏移量时,需要考虑像方的空间折射率。因此有:

式中:n1为光学面的像方空间折射率;是实际出射波阵面上光线的位置坐标。
一个光学面的三阶光线像差计算公式为
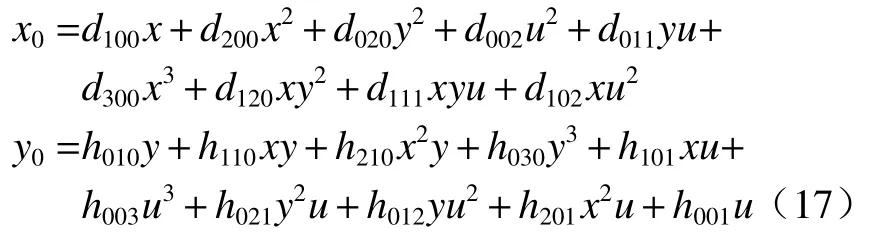
式中di jk和hi jk为 光线像差系数,具体公式由文献[8]中附录B 给出。
2.2 多元件光学系统的波像差计算
对于g个光学面的折反射组合光学系统,系统总的波像差是各光学面产生的波像差之和[14]。因此,在孔径光线传递为线性近似的条件下,光学系统总的波像差表达式为
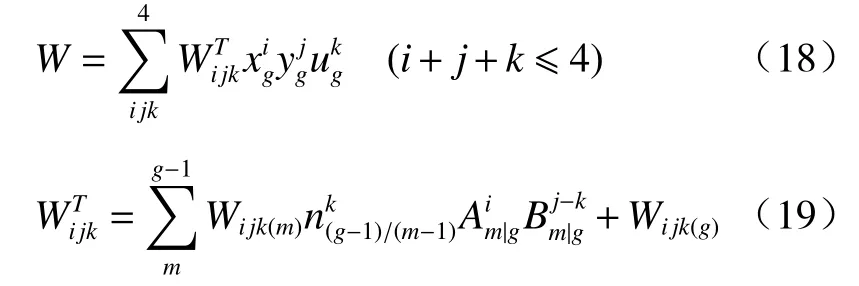
式中:Wijk(m)和是第m个 成像面和系统总的波像差系数。传递系数Am|g、Bm|g由 下式给出:
在计算像差系数的公式中,用wijk代 替其他相关光学系统参数为最后光学面像方空间的参数。
3 像差理论应用实例
综上所述,经扩展后的平面对称光学系统像差理论的像差表达式既适用于折射系统,也适用于反射系统。在像差的计算上,扩展后的表达式使两者保持了统一,仅需注意在计算折射系统时引入物像方的折射率作为计算参数即可。扩展后的像差理论表达式可以直接应用于折反射组合光学系统的像差计算,且光学系统元件的表面可以是多种二次旋转圆锥曲面。为了验证平面对称像差理论适用于光束斜入射的折反射组合光学系统,将其应用于椭球镜面形检测光学系统的成像计算,并与Zemax 软件[15]的光线追迹结果进行比较。
椭球镜面形检测光学系统光路示意图如图2所示,它是由一块椭球面反射镜OE1 与一块球面透镜OE2 组成(OE2 的作用主要是缩短光路长度)。假定激光光纤光源和像平面位置分别在S和S′处 , α、 β分别表示光束打在椭球镜上的入射角与反射角。

图2 椭球镜面形检测光学系统示意图Fig.2 Schematic diagram of surface-shape detection optical system of ellipsoidal mirror
椭球镜面形检测光路系统的相关光学参数由表1 给出,显然n0=n1=n3=1。

表1 椭球镜面形检测系统的光学参数Table 1 Optical parameters of surface-shape detection optical system of ellipsoidal mirror
下面将分别计算孔径光阑直径为7 mm 时,光束打在椭球镜面上的入射角分别为 0°、 40°、80°情况下D 光(工作波长为587.56 nm)的像差分布,并且假定激光光纤光源与椭球镜的距离为100 mm。
应用本文讨论的扩展后的像差理论以及光线追迹软件Zemax 分别计算该光学系统在像平面上的光线点列图,计算结果如图3 所示。图3 中最右边 α表示光束打在椭球镜上的入射角,图3(a)是应用光线追迹软件Zemax 得到的光线点列图,图3(b)为应用本文扩展的平面对称光学系统像差理论计算的像差分布图。由图3 可知,在不同斜入射角度情况下,无论是像差分布尺寸,还是点列图的形状特征,两种方法的计算结果都吻合得很好。

图3 椭球镜面形检测系统的光线点列图Fig.3 Ray of light spot diagrams of surface-shape detection optical system of ellipsoidal mirror
4 结论
本文讨论了基于平面对称反射光栅系统的像差理论,将其扩展为适用于光束斜入射的折射光学系统的像差分析,使得该像差理论可以对光束斜入射的折反射组合光学系统进行像差分析计算。然后,应用扩展的像差理论对椭球镜面形检测的折反射组合光学系统进行像差计算,并与光线追迹软件Zemax 模拟结果进行对比。结果表明:即使在大角度斜入射(甚至掠入射)的情况下,扩展后的平面对称光学系统的像差理论对此类光学系统的计算依然具有令人满意的计算精度。为光束斜入射的折反射组合光学系统的像差分析及优化设计提供了一种强有力的分析手段。

