硅基光学相控阵性能评估方法

张耀元，王 锐，姜瑞韬，杜坤阳，李远洋

（1.中国科学院 长春光学精密机械与物理研究所 激光与物质相互作用重点实验室，吉林 长春 130033；2.中国科学院大学，北京 100049）

引言

随着激光雷达在诸多领域的成功应用，对激光雷达各方面的要求越来越高。激光雷达的核心是激光扫描技术，近年来激光扫描技术快速发展，传统的激光扫描技术，例如，机械式[1]、声光式、电光式等一系列激光扫描技术均有其各自的局限性，因此光学相控阵就在微波相控阵的基础上应运而生。基于光学相控阵的扫描技术具有光波束扫描分辨率高、抗电磁干扰能力强、可集成小型化等优势[2]，目前对光学相控阵的具体研究分为若干类，包括光纤干涉型[3]、集成波导型[4]、微机电型[5]、液晶光学相控阵[6]等。绝缘体上硅（SOI）平台与互补金属氧化物半导体（COMS）工艺的高效兼容使得硅光子技术有利于实现大规模集成，因此基于硅光子平台的硅基光学相控阵[7-10]迅速成为研究热点。目前来看，针对光学相控阵特性参数包括扫描角度、速度和精度等能否达到预期目标还缺乏系统性的测试和分析，难以为相控阵优化设计提供有效的数据支撑，一定程度上阻碍了光学相控阵的大规模市场化。本文主要针对典型光学相控阵，深入分析硅基光学相控阵性能评估理论，并开展评估系统设计及评估方法研究工作。

1 性能评估理论研究

对光学相控阵的性能评估，需要对其各项特性参数进行细致的分析。而对所有特性参数的分析是基于对近远场衍射光斑图样的采集实现的，根据标量衍射理论，如图1（a）所示，对于一个在x1y1平面上有标量场e(x1,y1)的单独辐射孔径，沿z方向对距离为z1的x2y2平面的辐射结果通过菲涅尔衍射公式计算得：

式中： k 为传播常数，当z1足够大时，此时相位项趋近于零，由此得出远场辐射为近场辐射的傅里叶变换。

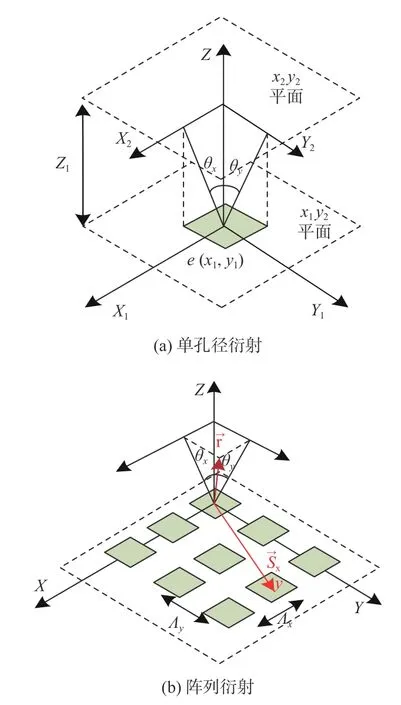
图1 单孔径衍射与阵列衍射示意图Fig.1 Schematic diagram of single aperture diffraction and array diffraction

基于单孔径衍射对二维等间距Nx×Ny天线阵列进行分析，如图1（b）所示， Λx和 Λy代表二维相控阵两个维度上单元的间距， θx和 θy分别代表传播光束与两个方向平面间的夹角。代表每个单元相对于坐标原点的位置矢量。代表传播光束的位置矢量[11]。推导得出阵列衍射分布：

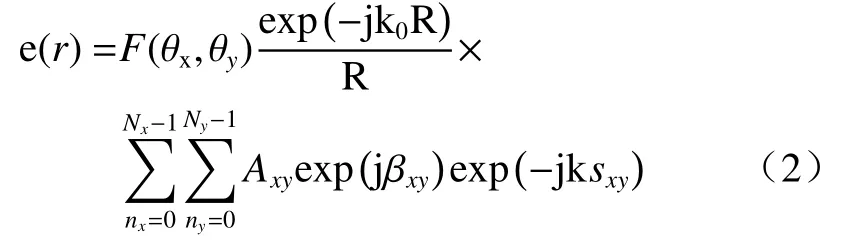
上式分为2 个部分，前项为每个独立单元在远场的衍射分布，称为元因子；后项为阵列间的相互作用，称为阵因子。为了实现光束扫描，需要在阵列中引入相位差βxy=nx·Δφx+ny·Δφy，使得光束发生偏转，化简得阵因子：

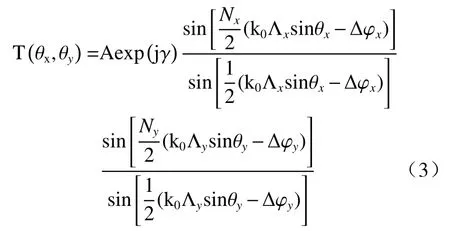
当阵列是由规则单元组成，即每个单元的尺寸均相同时，各个独立单元在远场的衍射相同，扫描的结果仅仅取决于阵因子。

2 性能评估系统设计

基于衍射理论对近远场成像系统进行设计，我们通过透镜加红外相机的傅里叶成像系统，将无限远的远场搬到透镜焦面上。设计的透镜结构对Thomas 等人[12]的方法做出了改进，如图2 所示。

图2 傅里叶成像系统Fig.2 Fourier imaging system

采用透镜共焦形成2 个中继4f 系统，使得近场成像放大15 倍，远场成像放大6 倍（F0=25 mm（NA=0.5），F1=150 mm，F2=F4=100 mm，F3=40 mm），加入分光镜使光束分两路同时观察近场远场成像。其中L0选择大的数值孔径以获得大范围视场，L2，L3，L4根据所需的放大率进行选择，不宜过大，应考 虑摄像头检测区域的限制。

3 性能评估方法研究

3.1 初始相位校准

光学相控阵是利用相位的变化来控制光束的偏转，在芯片生产中，很小的波导宽度变化也会导致很大的相位误差和混乱的远场图案，因此利用近场远场测试结构对天线相位进行校准必不可少[13]。目前来看，现有校准方案大多使用算法进行优化校准，单独使用算法校准通常很容易陷入局部最优。本文对与算法结合的物理干涉法[14]进行了改进设计，对天线阵列进行相位优化校准，具体流程如下 。

首先单独采集一个基准天线，加压使得天线附加相位从0 到2π 变化，使得该天线单元到达最大功率，并标记此时最佳衍射方向。第二步采集该单元与相邻单元天线以及对角线单元，调谐相应天线相位，使得中心干涉条纹对准标记最佳衍射方向，即对于基准天线最多校准8 个相邻天线。第三步对下一个基准天线以及相邻天线进行校准，直至全部天线单元校准完成。

使用多个基准天线的方式进行干涉校准，目的在于避免单基准天线校准过程中的误差放大，使得校准优化结果更趋近于理想值。校准时，需要人眼观测干涉条纹，调节施加电压以改变天线相位，令中心干涉条纹对准标记的最佳衍射方向，在调节过程中可能存在对中心干涉条纹的误判导致校准出现偏差。

3.2 偏转角度测试

光学相控阵的扫描范围通常情况下可定义为两个正负一级衍射阶次在远场上角度的差，根据（3）式，由Sinc 函数的最值条件，当T(θx,θy)中分子和分母同时为0 时，该式有最大值，推导得出此时x方向光偏转角度为

测试过程如图3 所示。首先使用角度尺与标准激光标定一块带有角网格的印刷屏幕，在此基础上将芯片发出的光斑打在印刷屏幕上，利用红外相机观察光斑在屏幕上的位置，可直接读取扫描角度。最大扫描角度在远场表现为主瓣与一阶栅瓣角度差，因此直接读取屏幕一阶旁瓣对应的偏转角度即相控阵芯片最大扫描角度。对角网格的标定与读数过程中，不可避免地会引入人为测量误差，使得测量结果出现一定的偏差，因此测量过程中需要根据相应测量精度要求，使用高精度测量仪器以减小误差。

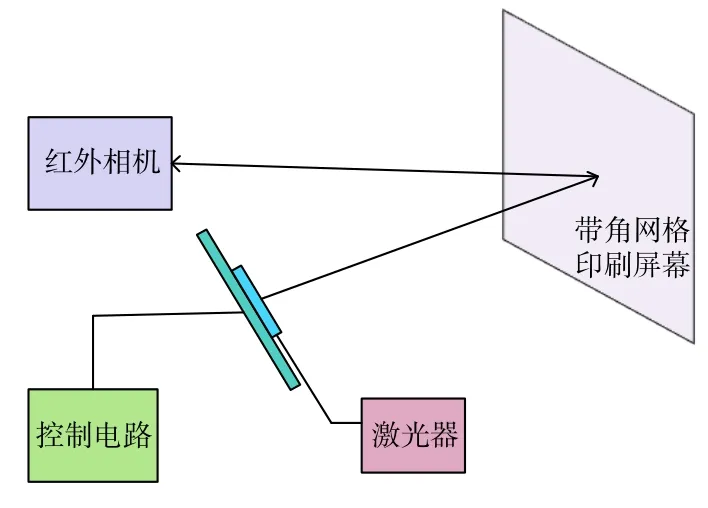
图3 扫描角度测试装置Fig.3 Scanning angle measuring device

3.3 扫描精度及准度测试

扫描精度是指系统可实现的最小扫描角度，即波束的步进角度。扫描精度越高，步进角度越小，在偏转范围内可扫描的角度数目越多，则空域扫描的分辨率就越高。

扫描准度是指对于相同的目标偏转角，光学相控阵多次偏转的实际角度与目标角度的误差大小，精度越高，表示光学相控阵系统的稳定性越好，扫描的准确度越高。

对扫描精度以及扫描准度的测试归根结底是对扫描角度的测试，利用图3 所示测试系统结构，根据不同测试要求对相应扫描角度进行测试分析即可得出。

3.4 主瓣宽度测试

对于均匀二维天线阵列，可以拆解为2 个维度上的多缝衍射模型，在X轴方向主瓣宽度（Y轴方向类似）为

由公式可得，在工作波长固定的情况下，主瓣宽度主要和波导数量，波导间距与远场光束的扫描角有关。测试过程同样利用如图3 所示测试装置，利用红外相机观察并读取角网格屏幕光斑大小，即可得出光斑角宽度。

3.5 扫描速度测试

光波导的扫描速率取决于相移区的调制速率，一般是通过对波导进行加热，利用热光效应进行相位调制，其主要原理是利用硅材料的折射率随温度变化的特性，实现对光相位的调制[15]。对于扫描速度的理论推导，需要对移相器进行热仿真，模拟电热转换过程，根据波导的温度变化求解有效折射率的变化，进而得到相应的相位变化，根据相位差能够求出光束在施加指定电压下光束的偏转角度，最后利用偏转角度除以理论控制电路的D/A 建立时间和放大器响应时间的和，即可求得理论扫描速度。

对扫描速度的测试需要利用红外相机加示波器的测试结构，采集当前接收到扫描光束信号的时间与相邻一次接收到扫描光束信号的时间差，即观察同一路信号的出现频率，利用测得最大扫描角度除以该时间差即为对应扫描速度。该测量过程除测量角度引入误差之外，主要误差存在于对示波器数据的提取过程中。

3.6 偏转效率测试

偏转效率定义为目标偏转光束的光强峰值与不发生偏转时的0 级光强峰值之比。

理论光学相控阵光强分布可由（2）、（3）式推导得出：

通过上式计算出指定偏转角 θ与0 级光强，即可求得系统理论偏转效率。

对偏转效率的测试首先需要利用红外相机接收并显示光斑位置，遮挡旁瓣，利用光功率计测量此时主瓣光强；其次施加电压使光束偏转目标角度；最后再次遮挡旁瓣测量偏转之后的峰值光强，利用（6）式即可得到偏转效率。该系统主要误差来源于测试过程中难以实现对旁瓣光束的完全遮挡，因此测量结果出现偏差。

3.7 探测距离测试

对于光学相控阵探测距离使用相干探测法，利用相干的激光信号和本地激光振荡信号发生干涉，对产生的拍频信号进行处理，在此基础上通过示波器分析得出探测距离。探测距离的测试结构如图4 所示。首先天线阵列发出信号光，经探测目标反射后通过接收天线接收；其次接收到的光波与本振光发生干涉，经跨阻放大器将光电流转化为电压；最后通过示波器进行分析得出探测距离。该系统主要误差来源为信号传输过程中存在其他信号源的干扰。

图4 探测距离测试装置Fig.4 Detection distance test device

4 结论

本文首先针对光学相控阵芯片性能评估理论进行了详细分析；在此基础上设计改进了傅里叶成像系统，同时对相控阵天线近远场动态图像进行观察分析。最后对光学相控阵建立了系统的评估方法研究，对相控阵天线初始相位进行了校准方案设计，利用改进的物理干涉法避免局部误差放大。针对扫描速度、角度、精度、准度、探测距离和远场主瓣宽度分别进行了理论分析，测试系统设计以及相应误差分析，能够对光学相控阵性能进行相对完善的性能评估。