动力触探杆长修正系数试验研究

左永振，程展林，丁红顺，廖建辉

（长江科学院 水利部岩土力学与工程重点实验室，武汉 430015）

1 引 言

在西部水电站开发中，河床覆盖层一般深达几十米至上百米，最深的近300 m，不同地质年代冲积或堆积而成的河床砂砾石覆盖层，物质组成复杂，空间变化大。深厚覆盖层的力学性质的确定是深厚覆盖层上建坝的关键技术问题之一，合理准确地确定覆盖层物理力学参数直接关系到工程造价和大坝安全。

由于河床覆盖层砂砾石为无黏性散体，深层取样困难，往往依据动探等原位测试技术勘探深厚覆盖层的工程特性，动探试验是根据打入的难易程度（表示为贯入度，指标定义为每贯入一定深度所需的锤击数）来判断土的工程性质。

在深厚覆盖层中进行动力触探试验，随着勘探深度的增加，所得锤击数N实际上受到了动力触探杆的长度影响，动力触探杆长度不同，锤击的效果不同，因此，必须进行锤击数的杆长修正。

对于动力触探杆长修正，长期以来，因无试验方法直接测定，存在两种理论，即牛顿弹性碰撞理论和弹性杆波动理论。

第1种杆长修正系数以牛顿碰撞理论为基础计算得到，并非实测。代表性的修正系数有《建筑地基基础设计规范》（GBJ7－89）[1]和《公路工程地质勘察规范》（JTJ064－98）[2]提到的上海顾季威有效能修正公式。

第 2种杆长修正系数以弹性杆波动理论为基础。代表性的修正系数有第一届贯入试验国际会议（ISOPT－1，1988）推荐的 SPT试验规程、美国ASTM《动力触探试验应力波能量量测的标准试验方法》（D4633－1986）[3]。

动力触探杆长各种修正系数的汇总见表 1。绘制的杆长修正系数与杆长的关系曲线见图 1。对比图1和表1，牛顿弹性碰撞理论和弹性杆波动理论得到的修正系数截然不同。牛顿弹性碰撞理论的杆长修正系数随杆长的增大而减小，而弹性杆波动理论的杆长修正系数却随杆长的增长而增大。因此，对杆长修正进行试验研究是有理论意义和实用价值的。

表1 各种杆长修正系数对比表Table 1 Modified coefficients for different rod lengths

图1 各种杆长修正系数与杆长的关系曲线Fig.1 Relation curves between rod length modification coefficient and rod length

上述的动力触探杆长修正系数，均与动力触探杆长是单一对应关系，《岩土工程勘察规范》（GB50021－2001）[4]和《建筑地基基础设计规范》（GB50007－2011）[5]给出了20 m范围内的重型动力触探锤击数修正系数，见表2。表中修正系数不仅与杆长相关，还与锤击数相关。

表2 锤击数修正系数Table 2 Modified coefficients for hammering counts

2 室内动力触探模型试验方法

2.1 试验系统设计

试验系统分为模型系统和原位测试系统两大部分。

模型系统由模型箱、加压系统组成，如图2、3所示。模型箱采用60 mm厚钢板焊接而成，内部尺寸为0.82 m×0.84 m×1.20 m（长×宽×高）。在模型箱内分层填筑试样，形成均质地基。加压系统为模型箱盖板与加压板之间置4个75 t千斤顶，采用自平衡对模型表面加压以模拟地基上覆自重应力。在盖板及加载板留同轴试验孔，以便进行动力触探试验。

图2 模型箱平面示意图（单位：mm）Fig.2 Plan of model box(unit: mm)

图3 模型箱剖面图（单位：mm）Fig.3 Section of model box(unit: mm)

原位测试系统依托11层的楼房楼梯间设置，如图4所示。在楼梯间底部放置模型系统，动力触探杆沿楼梯布置，动力触探锤击点安置在不同高度的楼层间，杆长分别为2.0、8.9、16.4、23.4、30.0、36.0 m。

针对一种地基土，根据同一种级配及干密度分层压实制成均质地基模型，在地基表面施加相同上覆压力（本次试验均为240 kPa，固结12 h），不同模型进行不同杆长下的动力触探试验，获得力学性质相同的地基模型的动探杆长与动探击数关系，进而得到不同杆长下的杆长修正系数。本方法是首次采用物理模型试验方法，直接测定杆长修正系数，成果可信，可验证理论的正确性。

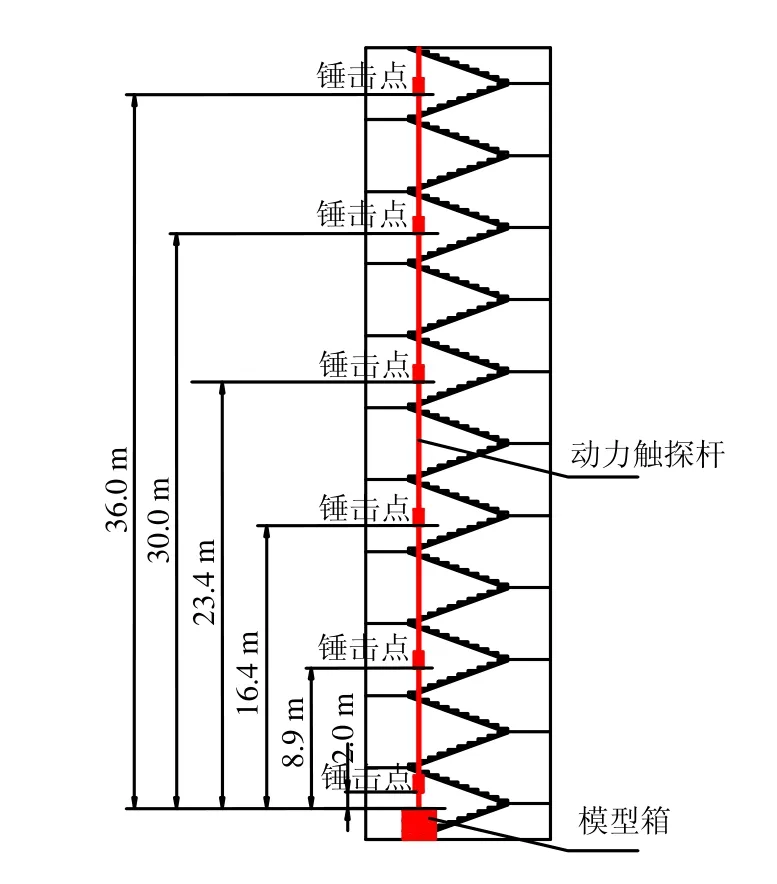
图4 动探锤击点布置图Fig.4 Distribution of hammering points of dynamic penetration

2.2 试验用料

本次共进行了两组试验，试验土样分别选取均质中粗砂和砂砾石料。

均质砂为粒径0.5～1.0 mm的中粗砂，最大干密度为1.63 g/cm3，最小干密度为1.31 g/cm3。试验干密度为1.45 g/cm3，对应相对密度为0.50，中密状态。

砂砾石料选取最大粒径为60 mm级配连续的砂砾石料，试验级配见图5。室内击实试验得到该级配下的最大干密度为2.31 g/cm3。试验密度为2.12 g/cm3，压实度为92%。

图5 砂砾石料试验级配Fig.5 Gradation of gravels during experiments

2.3 动力触探模型试验及数据整理

模型制作完成后，施加上覆压力并固结，进行动力触探试验。动力触探选用重型触探，总贯入深度不小于40 cm，记录每次锤击的贯入量，绘制锤击数与贯入深度的关系曲线，并对关系曲线稳定段进行曲线拟合，计算贯入100 mm时的锤击数，即为动力触探的锤击数N63.5。动力触探试验的代表性曲线见图6。

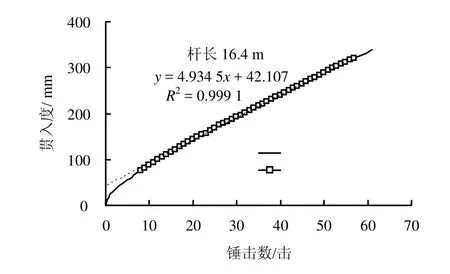
图6 动力触探试验代表性试验曲线Fig.6 A typical test curve of dynamic penetration

重型动力触探的试验步骤如下：

（1）试验前将触探架安装平稳，垂直度的最大偏差不超过2%，触探杆保持垂直连接牢固。

（2）贯入时使穿心锤自由下落，落距为0.76±0.02 m。

（3）锤击速率为每分钟15～30击，打入过程尽可能连续，所有超过5 min的间断都在记录中予以注明。

（4）及时记录每贯入0.10 m所需的锤击数，其方法是记录每一阵击的贯入度，再换算为每贯入0.10 m所需的锤击数。

（5）每贯入0.10 m所需锤击数连续3次超过50击时，即停止试验。

3 试验成果及分析

本次共进行了两组试验，每组试验的地基土试验级配、试验密度及上覆压力等试验条件均相同。其中地基土为均质砂的重型动探试验杆长分别为2.0、8.9、16.4、23.4、30.0 m，每个杆长进行了平行试验，有效点数为10点，得到的试验成果见表3；地基土为砂砾石的重型动探试验有效点数为11点，杆长分别为2.0、8.9、16.4、23.4、30.0、36.0 m，得到的试验成果见表4。

表3 均质砂动力触探试验成果Table 3 Dynamic penetration results in homogeneous sands

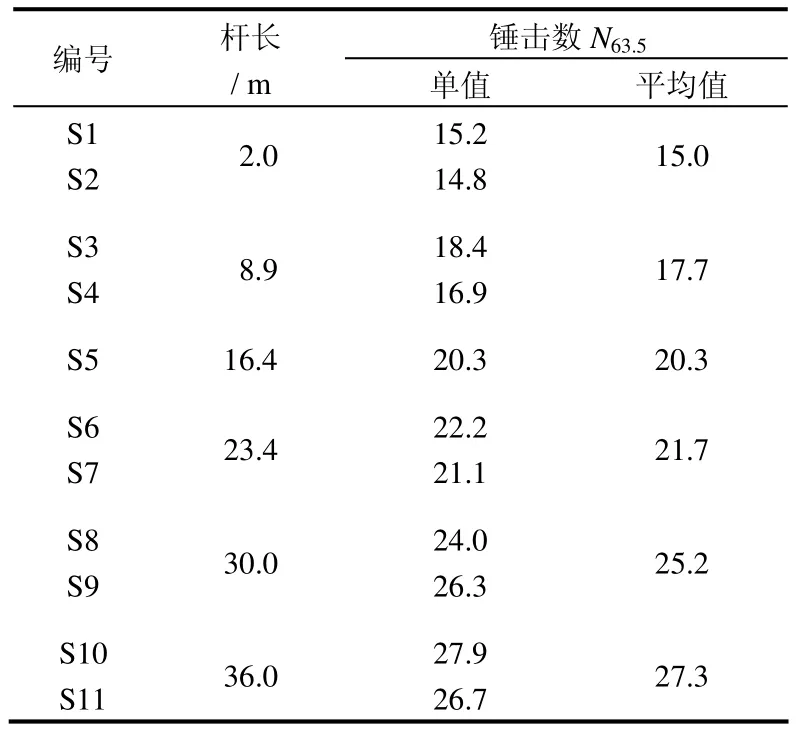
表4 砂砾石动力触探试验成果Table 4 Dynamic penetration results in gravels

由表3、4可见，每贯入100 mm的锤击数，随着动力触探杆长的增加，锤击数越来越大，例如砂砾石试验中杆长为2.0 m时的锤击数N63.5=15.0，杆长增加到36.0 m时的锤击数N63.5=27.3，增加了82%，这说明动力触探杆长对锤击数N63.5的影响是显著的。

在现行的动力触探试验杆长修正中，一般均是以杆长2～3 m为修正起点，本次试验成果分析中，假定杆长2.0 m时的锤击数N63.5是标准值，为修正起点，即将杆长2.0 m时的锤击数与杆长为i的锤击数的比值，作为不同杆长条件下的杆长修正系数。

均质砂和砂砾石的不同杆长下的杆长修正系数，如表5所示。

表5 均质砂和砂砾石动力触探杆长修正系数Table 5 Dynamic penetration rod length modification coefficients in homogeneous sands and gravels

将修正系数与杆长关系绘制在图7、8中，图中同时给出了牛顿弹性碰撞理论和弹性杆波动理论的修正系数。可见修正系数规律整体上符合牛顿弹性碰撞理论，与弹性杆波动理论的修正系数规律相反。修正系数基本符合《建筑地基基础设计规范》（GBJ7－89）和《公路工程地质勘察规范》（JTJ064－98）提到的上海顾季威有效能修正公式，且不同地基土的杆长修正系数基本一致。

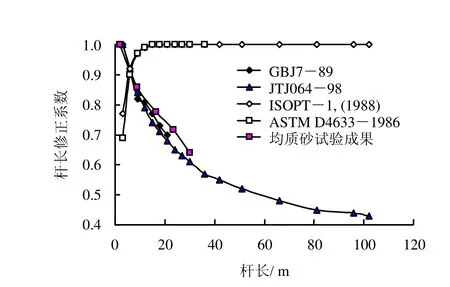
图7 均质砂杆长修正系数与杆长关系Fig.7 Relationships between rod lengths modification coefficients for homogeneous sands and rod length

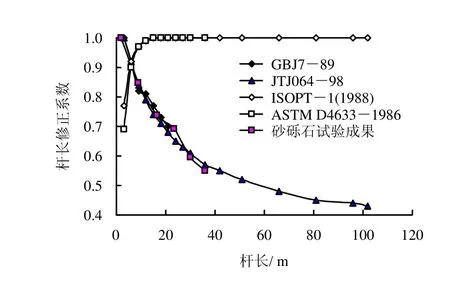
图8 砂砾石杆长修正系数与杆长关系Fig.8 Relationships between rod lengths modification coefficients for gravels and rod length

当在密实土层进行动力触探贯入试验时，常出现反弹，用手握紧动探杆，手会被震得麻木，说明能量损失很多[6]。动力触探的触探杆是接头连接，动力触探试验深度越深，触探杆的接头越多，动探杆产生的弯曲变形越大，在锤击中消耗的能量越多，达到相同的贯入深度需要的锤击数越多，相应的修正系数越小。

根据《岩土工程勘察规范》（GB50021－2001）的重型动力触探锤击数修正系数表（见表2），将本次试验成果进行杆长修正，并进行比较，见图9。

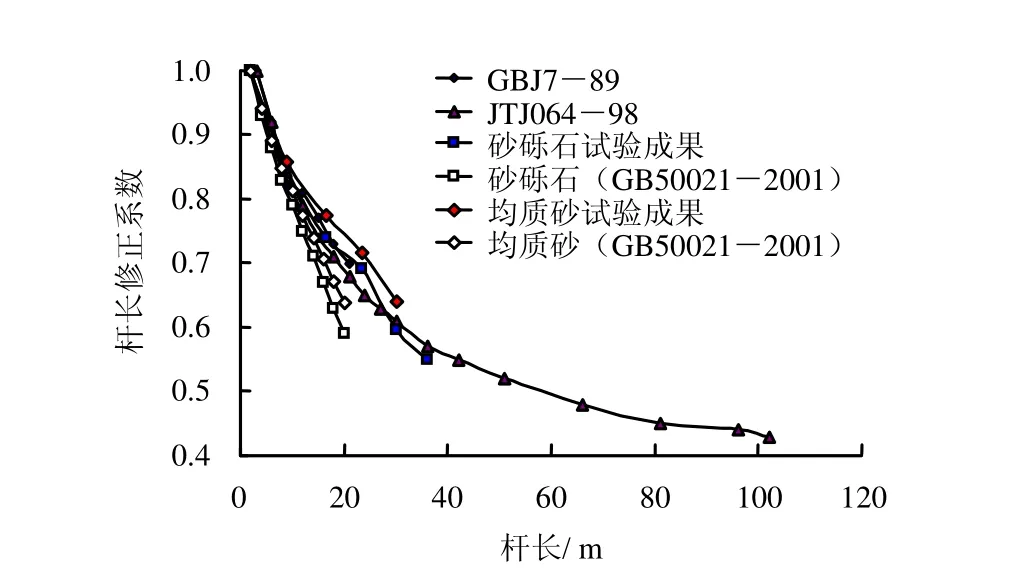
图9 砂砾石与均质砂杆长修正系数对比Fig.9 Comparison of rod length modification coefficients between gravels and homogeneous sands

由图可见，本次试验得到的杆长修正系数与《岩土工程勘察规范》（GB50021－2001）的修正系数差异性较大，本次得到的杆长修正系数明显大于规范推荐的修正系数，规范中修正系数实际上是对杆长、上覆自重压力、侧摩阻力的综合修正，而本次试验成果只考虑了杆长修正，因此，存在一定的差异性。而砂砾石和均质砂的动力触探杆长修正系数，差异性较小，说明不同材料下的杆长修正系数近似符合相同的规律。

4 结 论

（1）重型动力触探修正系数的整体趋势规律符合牛顿弹性碰撞理论，都随着杆长的增加，修正系数逐渐减小。

（2）修正系数基本符合《建筑地基基础设计规范》（GBJ7－89）和《公路工程地质勘察规范》（JTJ064－98）提到的上海顾季威有效能修正公式。

（3）本次试验的重型动力触探试验的最大杆长为36.0 m，超过杆长21.0 m的限制，但其N63.5值仍能有效地反映土的力学性质。

（4）砂砾石和均质砂的动力触探杆长修正系数差异性较小，表明不同地基土的杆长修正系数具有一致性。

[1]中华人民共和国建设部.GBJ7－89建筑地基基础设计规范[S].北京: 中国建筑工业出版社,1989.

[2]中华人民共和国交通部.JTJ064－98公路工程地质勘察规范[S].北京: 人民交通出版社,1999.

[3]ASTM D4633－86.Standard test method for stress wave energy measurement for dynamic penetrometer testing systems.Annual Book of Standards[S].Pbiladelphia:American Society for Testing and Materials,1986.

[4]中华人民共和国建设部.GB50021－2001岩土工程勘察规范[S].北京: 中国建筑工业出版社,2009.

[5]中华人民共和国建设部.GB50007－2011建筑地基基础设计规范[S].北京: 中国建筑工业出版社,2011.

[6]张平,田红花.有关动力触探影响因素修正问题的探讨[J].沈阳大学学报,1999,(2): 80－83.ZHANG Ping,TIAN Hong-hua.The study on amendment of dynamic sounding impact factors[J].Journal of Shenyang University,1999,(2): 80－83.