曲柄摇杆机构杆长的确定
李宏亮, 侯悦民, 黄民, 王雪雁
(北京信息科技大学机电工程学院,北京100192)
0 引言
在机构设计时,我们不但要了解机构的内在性能关系,而且要统筹各种性能指标,这样才能获得良好的设计。而在平面连杆设计中,各杆长度不同或点在连杆上的位置不同,连杆点的轨迹则不同,因此,平面连杆机构的设计主要是确定各杆长度比。各杆长度确定以后,各杆相应的运动规律也随之确定。所以,在设计平面连杆机构之前,我们应该首先进行平面连杆机构的运动分析。对平面连杆机构运动分析的方法有很多种(如解析法、图解法等)。本文主要采用了速度瞬心法进行了平面连杆机构的运动分析,在已知极位夹角θ和摇杆的两个极点C1、C2的情况下,利用三角形正弦、余弦定理计算出了各杆的长度,得出了不同传动角下的杆长比。
1 利用速度瞬心法进行平面连杆机构运动分析
平面连杆机构运动分析是为了了解机构的运动性能,用速度瞬心法[1-2]进行运动分析是十分方便的。在执行机构中,通常要求空回行程比工作行程快一些,以此来提高工作效率,这要求机构具有急回特性,所以,本文给出了极位夹角θ作为已知条件之一。用速度瞬心法进行平面连杆机构运动分析也主要是研究机构在极位时的特性。
设有一曲柄摇杆机构,曲柄AB为原动件,各杆之间直接通过转动副连接,所以,瞬心位置很容易直接确定(即位于各转动副A、B、C、D的中心处),分别记为P12、P23、P34、P41,然而,构件 2、4 对应的瞬心 P24不能直观地予以确定。但根据三心定理,对于构件2、3、4来说,P24必在P23及P34的连线上,而对于构件2、1、4来说,P24必在P12及P14的连线上,故上述两线的交点即为瞬心P24。瞬心位置如图1所示。
如果曲柄AB以等角速度ω2转动,便可以计算得出摇杆转动角速度 ω4、摇杆C点速度vc。

图1 曲柄摇杆机构及瞬心位置
因为已确定的瞬心P24为构件2、4的重合点,故有∶
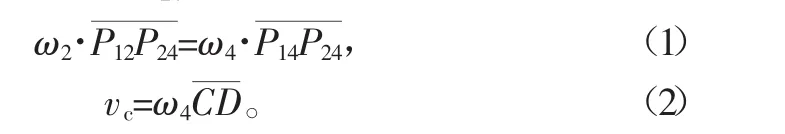
在较多平面连杆机构应用的场合中,摇杆的运动范围往往是已知的,那么就会在摇杆工作范围的两端形成两个摇杆的极限位置,分别对应着两个极位C1D、C2D。所以有

根据式(1),有
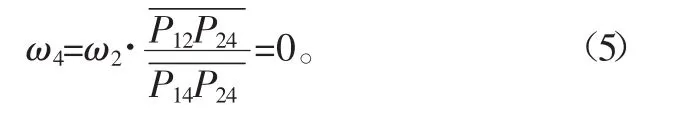
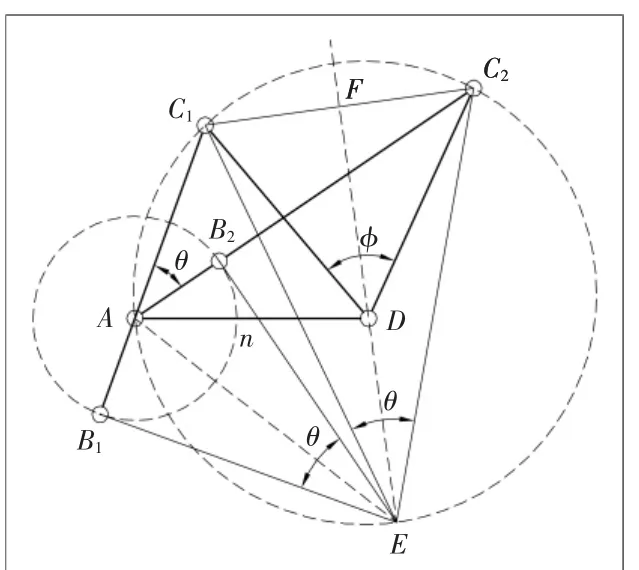
图2 转动极E
经分析,P14P24不可能为0,所以,只能,这样,就得出了瞬心P12和瞬心P24是重合的。所以,摇杆的极点 C1、C2与 A、B两点一定在同一条直线上。
因此,如果摇杆 的极点 C1、C2两点位置是已知的,我们可以选取其中一点任做一条不过另外极点的直线。在极位夹角θ或行程速比系数K确定的情况下,过另外一点做直线使其与水平线相交,两线交角为 θ。连接极点 C1、C2,过极点C1、C2确定直线的中点做垂线,那么点D必落在这条中垂线上。由此会设计出无限组连杆机构,得出的曲柄摇杆机构如图2所示。
在这无限组连杆机构中,有的因为不满足曲柄摇杆机构的杆长条件而被淘汰,有的会因不能保证机构传力性能良好而淘汰,这样就会得出部分合理的机构。然后,根据我们所需的设计参数,选择出合适的机构。
2 各杆杆长关系的确定[3-5]
通过上述分析,得出摇杆的极点C1、C2与A、B三点共线的结论,那么它们就会与杆1、杆4构成三角形。因此,我们可以通过三角形的余弦定理来确定各杆之间的关系,主要是利用机构在极位时的几何关系来建立的。设杆 2长为 a,杆 3长为 b,杆 4长为 c,杆 1长为H,摆角为φ,极位夹角为θ。
在△AC1C2中根据余弦定理有:
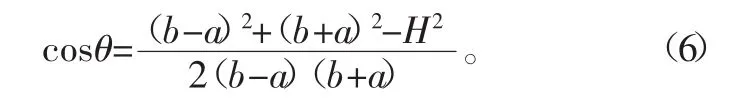
在△AC2D 中,设∠AC2D=β,则有:

其中,设∠B2C2E=α,β=α-(φ-θ)/2。
因为,在△EC2D中,根据三角形内角和为180°,很容易得出:

而在 Rt△AB2E 中,设 EB2=h,tan(θ/2)=a/h,则:

所以,在 Rt△EB2C2中,设 BE=h,则 tanα=h/b,故:

而在△DFC2中,因△DC1C2为等腰三角形,故

将式(13)左右两边同时除以2c,可得:
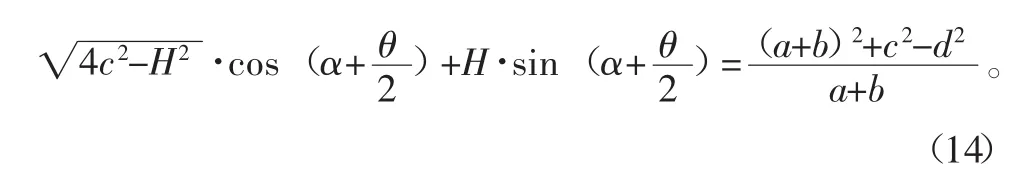

图3 最小传动角
在机构运行构成中,摇杆与连杆的夹角∠BCD的大小是变化的,该角即为传动角γ,为保证机构传动性能良好,应使 γmin≥40°~50°。对于曲柄摇杆机构,γmin出现在杆1与杆2共线处,如图3所示。


表1 杆长计算关系式
通过上面各式,在一些参数已知的情况下便可计算出各杆杆长。如果摇杆行程、极位夹角已知,我们可以根据要求自行选择传动角。那么根据上述关系式便可求出各杆杆长。现将部分情况列于表1。
3 利用计算机计算各杆杆长
根据前面建立各杆杆长关系式,我们通过编写程序求出了各杆杆长。已知曲柄摇杆机构的极位夹角θ=30°,摇杆的两个极点距离H=2.5m。传动角γ从40°开始以0.2°递增,在给定曲柄长度的情况下,根据式(6)、式(14)、式(15)计算出杆4和杆1的长度。
如果给定曲柄长度a=1.15 m,通过式(6)计算得出:b=2.214 8 m。通过式(14)、式(15)联立,可求出杆4长c、杆1长d。因为数据较多,绘制出在不同传动角情况下,杆4长c、杆1长d的数据曲线,如图4所示。
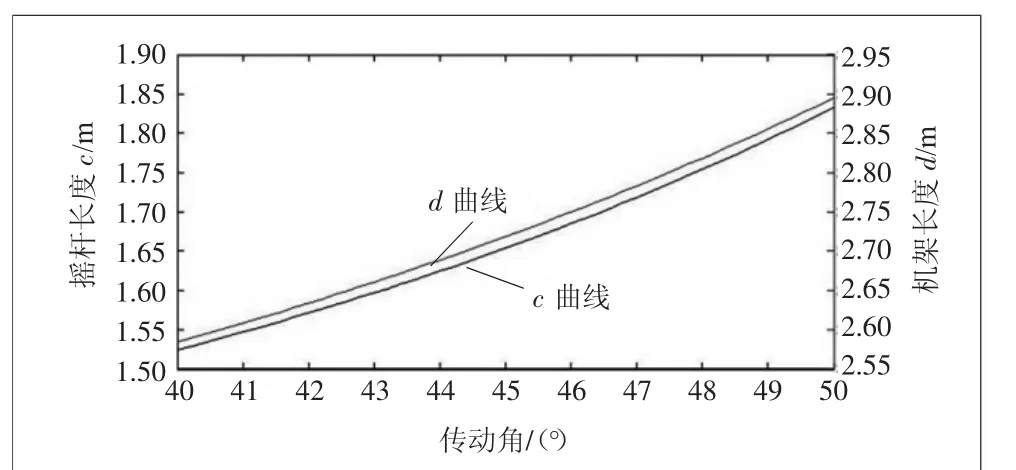
图4 杆长c、d数据曲线
我们知道,在设计时,应该注意铰链A点不能选在劣弧段上,否则机构将不能满足运动连续性要求。因为这时机构的两个极位DC1、DC2将分别在两个不连通的可行域内。所以我们在设计的时候,所得的β越大越好。而且,随着铰链A点的下移,传动角也越来越小,直至为0°,但为保证机构传动性能良好,应使 γmin≥40°~50°,因此,β 也会在相对应的范围内。
计算出各杆杆长以后,计算摆角φ、β的大小,摆角φ、β的数据曲线如图5所示。

图5 角β和摆角φ的数据曲线
4 结语
本文主要是在通过给定机构极位夹角和摇杆工作位置的情况下,通过简单的几何关系来研究曲柄摇杆机构各杆杆长,得出的各杆杆长可为曲柄摇杆机构的设计作为参考。但曲柄摇杆机构根据摇杆上下位置的不同,计算传动角γ的公式也不同。本文只采用了其中的一种进行了计算,而且是在其中一个杆长已知的情况下进行计算的。在现有的资料中,采用优化的方法进行设计是比较多的,但优化设计的方法极其复杂,而且,如果建立的模型不合理,或者选择的优化方法不准确,是很难计算出各杆杆长的。
[参考文献]
[1]孙恒.机械原理[M].北京:高等教育出版社,2006.
[2]李宏亮,郝静如.用瞬心法和解析法分析四杆机构急回特性[J].机械工程师,2012(2):21-23.
[3]华大年,华志宏.连杆机构设计与应用创新[M].北京:机械工业出版社,2008.
[4]谢伯康.曲柄摇杆机构图解综合的一种新方法[J].西安工业学院学报,1992(2):46-48.
[5]谢伯康,郭存娣.曲柄摇杆机构解析综合的通用杆长关系式[J].西安工业学院学报,1992(4):56-57.

