基于急转速度系数设计双曲柄机构研究
李玥晖
(武昌首义学院,湖北 武汉 430064)
0 引 言
近年来,随着计算机技术和各种现代设计方法的发展和应用,双曲柄机构的应用范围不断扩大。双曲柄机构的主要工作特点是存在急转速度特性,即主动曲柄作等速转动时,从动曲柄作变速转动。而笔者并未发现按急转速度系数设计的方法,因此笔者对此进行研究,最终得出一个较简单的创新方法:先将双曲柄机构转换为曲柄摇杆机构,再对曲柄摇杆机构进行设计,通过双曲柄机构和曲柄摇杆机构之间的几何关系,设计出双曲柄机构。
在转换为曲柄摇杆机构进行设计时,有一点需要注意:由于笔者要通过几何关系联系双曲柄机构和曲柄摇杆机构,因此设计曲柄摇杆机构是采用图解法。不求得到十分精确的解析值,重点是找到两种机构的关系。关于曲柄摇杆机构的图解法设计,如图1所示,按给定的急回要求设计曲柄摇杆机构:设已知摇杆的长度,摆角φ及行程速度变化系数K。首先根据θ=180°(K-1)/(K+1)得到极位夹角θ,并根据摇杆长度及摆角φ作出摇杆的两极位C1D及C2D,如图1所示。接下来确定固定铰链A的位置。作C2M⊥C1C2和∠C2C1N=90°-θ,C2M与C1N交于P;再作ΔPC1C2的外接圆,则圆弧C1PC2上任一点A都满足∠C1AC2=θ,所以固定铰链A应选在此弧段上。

图1 按急回要求以作图法设计曲柄摇杆机构
铰链A位置确定则需要给出其他的附加条件。如给定机架长度(或曲柄长度或连杆长度或杆长比或最小传动角),这时A点的位置已确定,曲柄和连杆也确定了,设计完成。另外在选择铰链A的位置时,不能选在劣弧段FG上,否则不满足运动连续性要求,若铰链A选在C1G,C2F两段弧上时,当A靠近G(F)时,机构的最小传动角将随之减小趋于零,故铰链A适当远离G(F)点较为有利。
1 双曲柄机构转换为曲柄摇杆机构
如图2,双曲柄机构在运动时可以转换为曲柄摇杆机构。双曲柄机构ABCD,机架长为d,主动曲柄长为a,连杆长为b,从动曲柄长为c,在运动过程中,主动曲柄和从动曲柄转角为α,φ。作辅助线AF并作ΔABF≅ΔAF′B′,再将ΔAB′F′旋转∠EAF′,得到ΔAEB2,连接DC1,B1E,由图2可见AD//B1E//F′B′,对比曲柄摇杆机构(图3)在极位的图形后就会发现双曲柄机构可以转换为曲柄摇杆机构,以及各个杆长的设计也转换为曲柄摇杆机构的设计。根据图2和图3得到B1E为b+d,B2E为b-d,曲柄摇杆机构中的摆角ψ为∠B1AB2,极位夹角θ为∠B1EB2。在双曲柄机构中对应相同的角。另外曲柄摇杆机构与双曲柄机构的杆长关系也一一对应:曲柄摇杆机构的机架对应双曲柄机构的从动曲柄,曲柄摇杆机构的摇杆对应双曲柄机构的主动曲柄,曲柄摇杆机构的机架对应双曲柄机构的主动曲柄,曲柄摇杆机构的连杆对应双曲柄机构的连杆,这样就确定了两者的几何关系:
∠BAB1=α,∠CDC1=∠FAE=φ
∠EAF′=π-φ
∠EAB2=∠F′AB′=∠BAF
∠B1AE=α-∠BAE,∠BAE=φ-∠F′AB′
∠B1AE=∠B1AB2+∠F′AB′
曲柄摇杆机构摆角=∠ψ=∠B1AB2=α-φ
ΔAB′F′旋转∠EAF′得到ΔEAB2,B1E//B′F′
∠EAF′=∠B1EB2
曲柄摇杆机构极位夹角=∠θ=∠B1EB2=π-φ
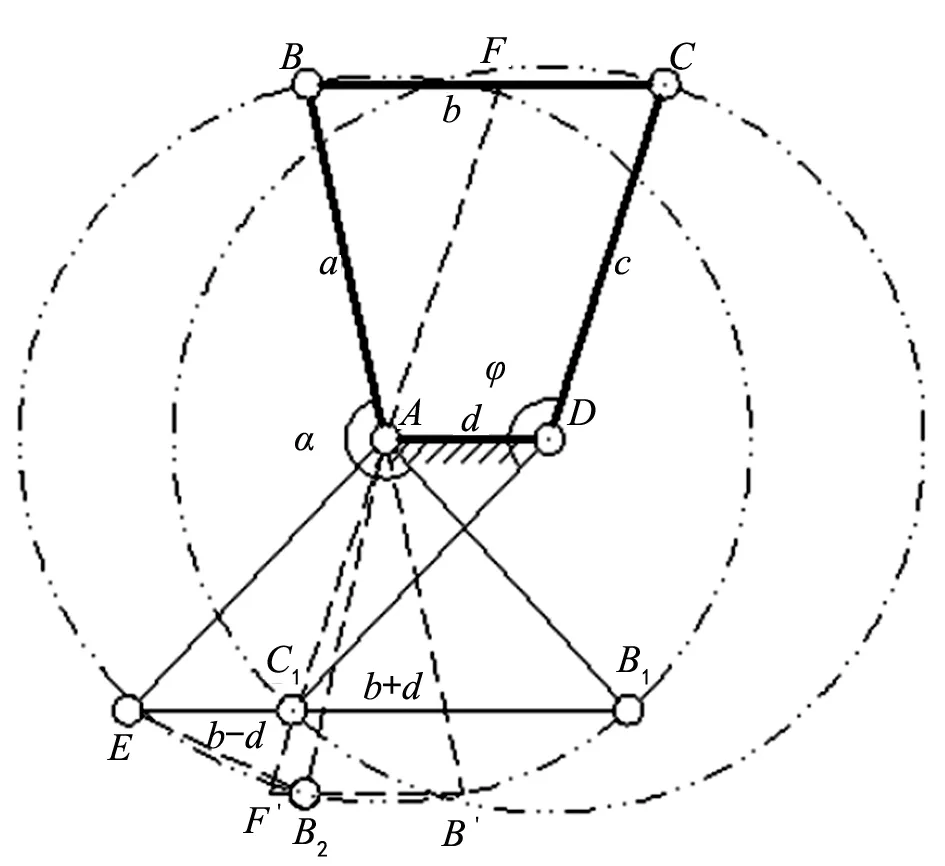
图2 双曲柄机构转换图

图3 曲柄摇杆机构
这样可以根据双曲柄机构的主动曲柄转角和从动曲柄转角确定曲柄摇杆机构的摆角和极位夹角,从而设计曲柄摇杆机构,再将其转换为设计双曲柄机构。完成设计。这里还有一种方法,在转换双曲柄机构时,连接DF,作AB的平行线,随后得到ΔDCF,同理作对称并旋转,找出几何关系,这种方法可以得到曲柄摇杆机构的极位夹角为α-π,但是不能保证极位夹角为锐角,因此不采用这种方法进行转换。
2 证明双曲柄机构与曲柄摇杆机构的几何关系
已知α,φ用图解法设计双曲柄机构
作法:选比例尺,作∠AEB1=α-φ,AE=AB1=a。
作rtΔFEB1,∠EFB1=π-φ
以FB1为直径作圆M
在圆M上取一点G连接GE,GB1,GA,则:
GE=b-d
GB1=b+d,GA=c⟹
证明:四边形ABCD为一主动曲柄AB长度为a,连杆BC,长度为b,从动曲柄CD,长度为c,机架AD,长度为d,的双曲柄机构。

作AI//DC,AG//C1D,则BI=b-d,GB1=b+d

图4 双曲柄机构运动规律
作ΔABI≅ΔAKJ令∠CDQ=φ0,∠BAQ=α0则∠BAI=α0-φ0
在ΔGAB1中,
∠GAB1=钝∠IAB1-∠IAG
=∠IAB+钝∠BAB1-∠IAG
=α0-φ0+α-∠CDC1=α0-φ0+α-φ
由ΔABI≅ΔAKJ可以得到:
BI=JK=b-d,∠JAK=∠BAI=α0-φ0,JK//GB1
∠JAG=π-∠IAG=π-∠CDC1=π-φ
将ΔAJK顺时针旋转π-φ后成为ΔAGE
则∠B1GE=π-φ,GE=JK=BI=b-d
∠AEB1=∠EAB1-∠GAE=α0+α-φ-φ0-∠JAK
=α0+α-φ0-φ-(α0-φ0)=α-φ
综上所述GB1=b+d,GE=b-d,AG=c,AB=a
于是求得了双曲柄机构与曲柄摇杆机构的几何关系以及证明了双曲柄机构在运动过程中可以转换为曲柄摇杆机构。
3 实 例
设已知双曲柄机构急转速度系数k为2.5,主动曲柄的长度,从动曲柄的长度,主动曲柄在运动到和机架,连杆平行时所转过的角度为210°。试设计双曲柄机构。
采用图解法设计曲柄摇杆机构,已知双曲柄机构从动曲柄的长度,转换为曲柄摇杆机构的摇杆。设计时先根据摆角和摇杆确定两个极位。在确定另一铰链位置时,给定曲柄摇杆机构的机架长度即双曲柄机构中的主动曲柄的长度,通过这一条件确定铰链位置,则设计出曲柄摇杆机构。
随后将曲柄摇杆机构转换为双曲柄机构:双曲柄机构的主动曲柄和从动曲柄为已知,双曲柄机构的连杆对应曲柄摇杆机构的连杆,双曲柄机构的机架对应曲柄摇杆机构的曲柄,这样就完成了双曲柄机构的设计。
4 结 语
基于急转速度系数设计双曲柄机构的方法进行研究,找到了一种创新方法,其中心思想在于联系曲柄摇杆机构和双曲柄机构,通过设计曲柄摇杆机构,再将其转换为双曲柄机构来完成设计过程。由于曲柄摇杆机构的设计方法较多,而这里只列举了一种方法,主要为了证明其转换关系及方法的实用性。实际上,在设计时可以采用任一方法设计曲柄摇杆机构,当完成设计后,转换为双曲柄机构即可。

